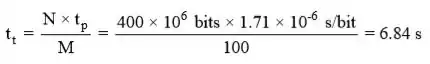Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 5.Problemas - Ex. 41

No armazenamento termomecânico de dados, uma cabeça de processamento, constituída por M pontas aquecidas, é usada para escrever os dados sobre um meio polimérico de armazenamento. Há microaquecedores por resistência elétrica em cada cabeça de gravação, que continuamente se deslocam sobre a superfície do meio. Os aquecedores são ligados e desligados através do controle da corrente elétrica para cada braço. Quando um braço passa por um ciclo completo de aquecimento e resfriamento, o polímero abaixo dele é amolecido e um bit de dados é escrito na forma de um furo na superfície do polímero. Uma trilha de bits de dados individuais (furos), cada um separado por aproximadamente 50 nm, pode ser feita. Múltiplas trilhas de bits, também separadas por aproximadamente 50 nm, são então esculpidas na superfície do meio de armazenamento. Seja um único braço que é fabricado com silício com uma massa de 50   ×   10 - 18   k g e uma área superficial de 600   ×   10 - 15   m 2 . O braço está inicialmente a T i   =   T ∞   =   300   K e o coeficiente de transferência de calor entre o braço e o ambiente é de 200   ×   103   W / ( m 2   ·   K ) .

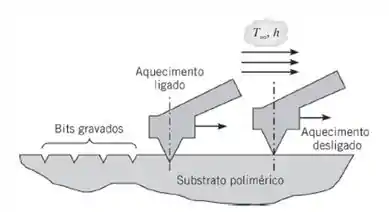
(a) Determine o aquecimento ôhmico requerido para elevar a temperatura do braço para T = 1000 K em um tempo de aquecimento de t a   =   1   μ s . Sugestão: Veja o Problema 5.20.

(b) Ache o tempo requerido para resfriar o braço de 1000   K para 400   K (tr) e o tempo de processamento térmico requerido para um ciclo de aquecimento e resfriamento completo, t p   =   t a   +   t r .  

(c) Determine quantos bits (N) podem ser escritos em um meio polimérico de armazenamento de 1 mm × 1 mm. Se M   =   100   braços são montados em uma única cabeça de processamento, determine o tempo total de processamento térmico necessário para escrever os dados

Passo 1

Vamo lá galera! (a) A partir do Problema 5.20 notamos que,

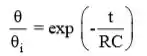
Onde o θ   ≡ T - T ( ∞ ) e T ∞ é a temperatura de estado estacionário correspondendo a t →   ∞ .

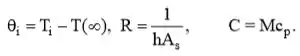
Logo,

Portanto, a primeira equação pode ser avaliada como,

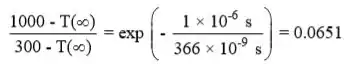
Logo, T ∞ = 1049   K . Em estado estacionário, temos:

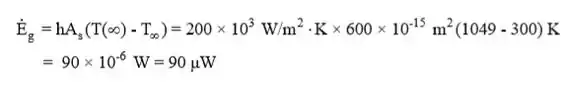
Passo 2

(b) A equação 5.6 pode ser usada. Daí,

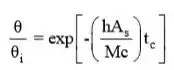
Portanto,

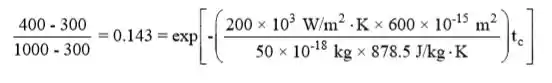
Passo 3

(c) Cada bit ocupa,

Portanto, o número de bits em um substrato de 1 mm × 1 mm é

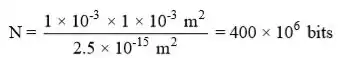
O tempo total necessário para escrever os dados ( t t ) é,

e

Resposta

a ) E g = 90   μ W

b ) t c = 0.71   μ s ,     t p = 1.71   μ s

c ) N = 400   × 10 6   b i t s ,     t t = 6.84   s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um tarugo de madeira cilíndrico ( k = 0,17W / m ⋅ Keα = 1,28 × 10 - 7m 2 / s ) tem 10c m de diâmetro e está inicialmente na temperatura uniforme de 25 ℃ ℃. É exposto a gases quentes a 600 ℃ ℃ na larei
Um dispositivo eletrônico dissipando 18W tem massa de 18g , calor específico de 850J / k g ⋅ K e área de 4c m 2 . O dispositivo é usado levemente, ficando ligado por 5 minutos e depois desligado por v
Um tijolo de dimensão 203 × 102 × 57m m é queimado em um forno a 1.100 ℃ ℃ e depois resfriado em uma sala à temperatura ambiente de 30 ℃ ℃ com coeficiente de transferência de calor de convecção de 5W
Bolas de aço de carbono ρ = 7.833k g / m 3 ,k = 54W / m ⋅ K ,c p = 0,465k J / k g ⋅ Keα = 1,474 × 10 - 6m 2 / s de 8m m de diâmetro são recozidos por aquecimento a 900 ℃ ℃ em forno e, depois, esfriado
Barras de aço ( ρ = 7.832k g / m 3 ,c p = 434J / k g ⋅ Kek = 63,9W / m ⋅ K ) são aquecidas em um forno a 850 ℃ ℃ e depois mergulhadas em banho-maria a 50 ℃ ℃ por um período de 40 segundos como parte d