Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Mecânica dos Fluidos- Ed: 1º - Capítulo 7.Problemas - Ex. 100
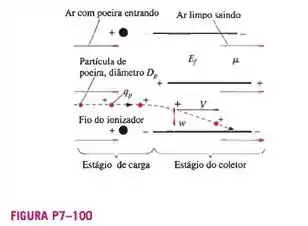
Um precipítador eletrostátíco (ESP) é um dispositivo usado em diversas aplicações para limpar o ar carregado de partículas. Em primeiro lugar, o ar empoeirado passa através do estágio de carga do ESP, onde as partículas de poeira recebem uma carga positiva (coulombs) dos fios do ionizador carregado(Figura ). Em seguida, o ar empoeirado entra no estágio de coletor do dispositivo, onde escoa entre duas placas com cargas opostas. A força do campo elétrico aplicado entre as placas é (a diferença de voltagem por unidade de distância). A Figura P7-100 mostra uma partícula de poeira carregada com diâmetro Dp. Ela é atraída para a placa com carga negativa e se move na direção daquela placa a uma velocidade chamada de velocidade de deriva w. Se as placas forem suficientemente longas, a partícula de poeira se choca com a placa com carga negativa e adere a ela. O ar limpo sai do dispositivo. Acontece que para partículas muito pequenas a velocidade de deriva só depende de , , , e da viscosidade do ar, .
- Gere uma relação adimensional entre a velocidade de deriva através do estágio coletor do ESP e os parâmetros dados. Mostre todo o seu trabalho,
- Se o a força do campo elétrico dobrar, com todas as outras condições iguais, por qual fator a velocidade de deriva variará?
- Para determinado ESP, se o diâmetro da partícula dobrar, com todas as outras condições iguais, por qual fator a velocidade de deriva variará?
Passo 1
Vamos lá! Eu sei que o enunciado assusta, mas isso nada mais é do que uma questão que envolve análise dimensional e semelhança!!!
Vamos começar a nossa letra a então!!
- Gere uma relação adimensional entre a velocidade de deriva através do estágio coletor do ESP e os parâmetros dados.
- Se o a força do campo elétrico dobrar, com todas as outras condições iguais, por qual fator a velocidade de deriva variará?
Como eu falei, assusta, mas todos os parâmetros estão no enunciado!!!
Pra começar, vamos listar as variáveis relavantes:
Daqui a gente já consegue ver o número de parâmetros, que são , então:
Agora a gente precisa listar as dimensões primárias de cada parâmetro!
Vamos começar por :
Agora a carga, :
A força do campo elétrico, que nada mais é do que uma tensão:
A viscosidade do ar, :
E por fim o diâmetro da partícula, :
Quando a gente listou as dimensões primárias de cada parâmetro a gente usou as dimensões e I , então podemos considerar:
Teorema de Pi de Buckingham:
O a gente já tinha achado no Passo 1, lá vimos que !
Substituindo:
Nesse caso o número de grupos esperado é igual a . Então vamos atrás dele!!
Para isso, precisamos decidir quais vão ser os parâmetros repetidos.
Temos e , como é o parâmetro dependente a nossa única opção é escolher e como parâmetros repetidos.
Agora sim, vamos encontrar o nosso grupo !!
Organizando os nossos parâmetros a gente fica com:
Eles tem que ter dimensão zero, como a gente ta vendo no lado esquerdo da igualdade! Agora vamos substituir esses parâmetros pelas suas respectivas dimensões primárias!
Agora vamos equacionar os expoentes de uma dimensão de cada vez, começando por corrente:
Corrente:
Massa:
Podemos dizer também que:
Tempo:
Logo:
Comprimento:
Então ficamos com:
Agora que a gente conhece os expoentes, vamos substituir:
Organizando:
Como só temos um grupo ele não pode ser função de outros grupos , logo dizemos que ele é igual a uma contante:
Com isso a relação que o enunciado pediu, fica:
Passo 2
Agora que a gente conhece a relação entre com as outras variáveis do ciclone, podemos responder a letra b!
Que é:
Então vamos pegar a relação que terminamos de ver:
Como apenas e variam a gente pode fazer a seguinte igualdade:
Sabendo que a força do campo elétrico vai dobrar, escrevemos:
Agora arrumando:
É isso ai!! Quando o a força do campo elétrico dobra também dobra!!
Passo 2
Agora para a letra c o raciocínio é bem parecido!
Para determinado ESP, se o diâmetro da partícula dobrar, com todas as outras condições iguais, por qual fator a velocidade de deriva variará?
Como o diâmetro dobra, fazemos:
Logo a a velocidade vai diminuir pela metade!
Resposta
(a) ;
(b) vai aumentar em um fator de;
(c) vai diminuir em um fator de .