Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Çengel - Transferência de Calor- Ed: 4º - Capítulo 7.Problemas - Ex. 16
A pressão atmosférica em Denver, colorado (altitude 1610 m) é 83,4 KPa. O ar nessa pressão e 30ºC escoa com velocidade de 6 m/s ao longo de uma placa plana de 2,5m x 8m a uma temperatura de 120ºC. Determine a taxa de transferência de calor a partir da placa considerando que o ar escoa paralelo no (a) lado de 8m de comprimento e (b) lado de 2,5m.
Passo 1
Incialmente quando você lê o problema parece que ele vai ser difícil, né? Mas não se assute, ele está pedindo “mais do mesmo” tanto na letra (a) quanto na letra (b).
Tá, mas tipo, se você olhar, nesse problema ele nos deu a pressão do ar atmosférico e não pode ter sido atoa, certo?
Certíssimo!
Aqui vem uma dica pra você, quando é dado a pressão em um problema desse tipo, costuma ser pra gente ter que preliminarmente encontrar o valor de viscosidade cinemática primeiro. E é bem simples de fazer, sabe como?
Lembra sempre que viscosidade cinemática é INVERSAMENTE PROPORCIONAL a pressão.
De forma matemática, podemos escrever isso aqui:
Onde esse @atm indica que você deve ter o valor da propriedade em 1 atm e pi representa no subíndice a viscosidade cinemática na pressão que você se encontra!
E essa Patm é a pressão dada no problema, mas que vamos passar de Kpa para atm, belê?
Logo,
Depois desse pulo do gato, a questão fica super tranquila e metódica!!!
Passo 2
Vamos olhar a primeira situação.
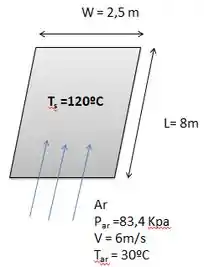
O enunciado está pedindo para calcularmos a taxa de transferência de calor entra a superfície e o fluido, e, lembrando bem, o mecanismo de troca térmica entre sólido e fluido é CONVECÇÃO, então a gente escreve que:
A única varíavel que falta termos o valor para calcular q é o coeficiente de troca térmica convectivo! Mas antes, vamos pegar os valores das propriedades em Tf (temperatura de filme), ok?
(calculamos lá no início da questão)
Passo 3
Vamos calcular em qual regime estamos!
A gente sabe que acima de 5 x 105 para uma placa plana, passamos do Reynold crítico e estamos no regime turbulento! PORÉM, a maioria dos livros nos aconselham que quando temos esses valores muito próximos ainda de 105 é bom usarmos as correlações de escoamento combinado, ok?
E a correlação mais apropriada para o problema é:
Vamos substituir isso na nossa equação da taxa.
A = 8m x 2,5m
h = 10,05 W/m²K
Ts =120ºC
Tar= 30ºC
Passo 4
Vamos repetir o mesmo procedimento para a situação (b)
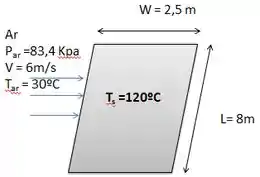
Calcular reynold:
Escoamento combinado.
Calcular h com a correlação apropriada:
IMPORTANTE: Importante perceber que a unidade W/m²K = W/m²ºC , pois a variação de 1ºC é igual a variação em 1K.
Calcular q:
Isso faz sentido lógico e físico!
Pensa comigo:
Se você tem um maior “caminho” disponível para trocar calor, você terá por um valor maior de h e q para as mesmas condições e por consequência uma taxa de transferência de calor maior também!
Resposta
- q = 18100 W (b) q = 12920 W