Exercícios de Escoamento em Placa Plana - Lista de Exercícios Resolvida

Placas de aço (AISI 1010), de espessura e lados de comprimento , são transportadas na saída de um processo de tratamento térmico e simultaneamente resfriadas por ar atmosférico com velocidade e em escoamento paralelo sobre as placas.

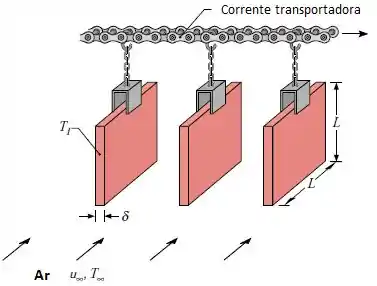
Para uma temperatura da placa inicial de , qual é a taxa de transferência de calor saindo da placa? Qual é a taxa de variação da temperatura da placa correspondente? A velocidade do ar é muito maior do que a velocidade da placa.

Uma placa plana de de espessura feita de chumbo (com propriedades constantes e dadas pelo valor dessas a ) está com uma de suas faces sob uma chama que fornece a ela . A placa é quadrada com de lado. Pela outra face, uma corrente de ar a escoa paralelamente a . O sistema está a .

Se for possível, em quanto tempo a temperatura vai atingir ? Se não for possível atingir , qual é a temperatura máxima da placa?

Assuma modelo de parâmetros concentrados para resolver o problema.

As propriedades termofísicas do ar são dadas na tabela.

Uma placa plana quadrada de de lado tem uma de suas faces imersa em um meio com ar a que escoa paralelamente a placa com uma velocidade de . A outra face está exposta a uma chama. Essa chama está a e um coeficiente de película de pode representar a transferência de calor homogênea na área dessa face.

A placa é feita de aço inoxidável 304, as propriedades do aço podem ser consideradas constantes e iguais a seus valores a e essa placa possui uma espessura de .

Considerando que o sistema está em estado estacionário e que a radiação térmica pode ser desprezada. E sabendo que as propriedades termofísicas do ar podem ser obtidas pela tabela anexa do livro de referência e que esse se comporta como gás ideal.

Determine a temperatura na superfície de cada face da placa e a taxa de transferência de calor associada ao sistema.

A superfície de um coletor solar pode ser considerada como uma placa plana, com dimensões de . A temperatura desta superfície é praticamente uniforme e de .

Ar a escoa sobre a placa ao longo de seu comprimento, com velocidade de . Calcule:

Coeficiente médio de transferência de calor sobre a placa;

Coeficiente local de transferência de calor em ;

Fluxo de calor local em ;

Taxa de calor trocado entre a placa e o ar.

(Adaptada) Considere uma aleta retangular que é usada para resfriar o motor de uma motocicleta. A aleta possui de comprimento e está a uma temperatura de , quando a motocicleta desloca-se a uma velocidade de em ar a .

O ar encontra-se em escoamento paralelo às superfícies da aleta e condições de escoamento turbulento podem ser admitidas ao longo de toda a superfície.

Qual é a taxa de remoção de calor por unidade de largura da aleta?

Uma placa plana, com largura de , é mantida a uma temperatura superficial uniforme pelo uso de módulos retangulares geradores de calor, com espessura e comprimento , que são controlados independentemente. Cada módulo encontra-se isolado de seus vizinhos, bem como em sua superfície inferior.

Ar atmosférico a escoa sobrea a superfície da placa a uma velocidade de . As propriedades termofísicas dos módulos são , e .

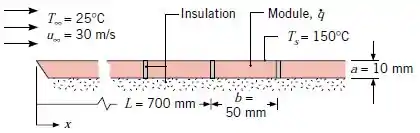
Determine a geração de energia necessária, , em um módulo posicionado a uma distância de da aresta frontal.

Determine a temperatura máxima neste módulo de geração.

O número de Nusselt médio no escoamento laminar sobre uma superfície plana rugosa de comprimento igual a 1m, é dado por:

Determine qual dentre dois fluidos (A e B) deve ser escolhido para resfriar a placa, considerando que a taxa de calor transferido deve ser a mesma com os dois fluidos. Justifique sua resposta. As propriedades dos fluidos são dadas na tabela abaixo:

(Adaptado) No processo de secagem de duas superfícies de mesmas dimensões (comprimento e largura ), mas com diferentes rugosidades, o regime de escoamento do ar sobre a superfície (na direção longitudinal) é turbulento.

As temperaturas das superfícies são , e longe dela a temperatura do fluido é . Na superfície 1, o coeficiente de troca de calor é dado por: ; e na superfície 2, , todos os valores em unidades SI. Para as duas situações, determine:

O número de Nusselt médio nas superfícies, .

Determine a taxa de calor total trocado por cada placa .

Cem componentes elétricos, cada um dissipando , estão fixados a superfície de uma placa quadrada de cobre , e toda a energia dissipada é transferida para a água que se encontra em escoamento paralelo sobre a superfície oposta.

Uma protuberância na aresta frontal da placa atua na perturbação da camada-limite e a placa pode ser considerada isotérmica. A velocidade e a temperatura d água são e , e as propriedades termofísicas da água podem ser aproximadas por , e .

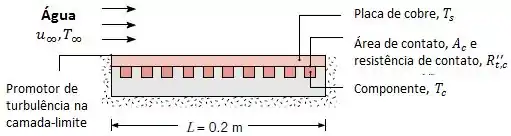
Qual é a temperatura da placa de cobre?

Se cada componente possui uma área superficial de contato com a placa de cobre igual a e a resistência térmica de contato é igual a , qual é a temperatura dos componentes? Despreze a variação de temperatura ao longo da espessura da placa de cobre.

(Adaptada) Seja uma placa plana sujeita a um escoamento paralelo (superior e inferior) caracterizado por , .

Determine os coeficientes de transferência de calor por convecção médios e as taxas de transferência de calor por convecção associadas a uma placa plana com um comprimento e largura , para o escoamento de ar e temperaturas superficiais e .

Determine os coeficientes de transferência de calor por convecção médios e as taxas de transferência de calor por convecção associadas a uma placa plana com um comprimento e largura , para o escoamento de água e temperaturas superficiais e .