Enunciado
FenTrans, MecFlu, TransCal e TransMassa - Incropera - Fundamentos de Transferência de Calor e Massa- Ed: 7º - Capítulo 7.Problemas - Ex. 31
Na produção de folhas metálicas ou plásticas, é costume resfriar o material antes que ele deixe o processo de produção para armazenamento ou embarque para o cliente. Tipicamente, o processo é contínuo, com uma folha de espessura e largura sendo resfriada enquanto transita por uma distância L e com uma velocidade V entre dois rolos. Neste problema, consideramos o resfriamento de aço carbono não ligado por uma corrente de ar, que se move a uma velocidade em escoamento cruzado sobre as superfícies superior e inferior da folha. Um promotor de turbulência é usado para propiciar um desenvolvimento de camada-limite turbulenta sobre toda a superfície.
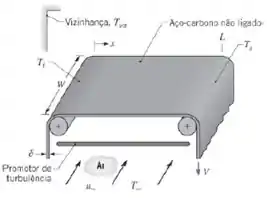
- Aplicando a conservação de energia em uma superfície de controle diferencial de comprimento , que se move com a folha ou é estacionária e através da qual a folha passa, e supondo uma temperatura da folha uniforme na direção do escoamento do ar, deduza uma equação diferencial que governe a distribuição de temperatura , ao longo da folha. Considere os efeitos radiantes, assim como os convectivos, e escreva o seu resultado em termos de velocidade, da espessura e das propriedades da folha , do coeficiente convectivo médio associado ao escoamento cruzado e as temperaturas ambientes .
- Desprezando a radiação, obtenha uma solução em forma fechada para a equação anterior. Para , , , , , , e uma temperatura da folha no início do resfriamento de , qual é a temperatura na saída ? Suponha influência desprezível da velocidade da folha no desenvolvimento da camada-limite do escoamento do ar. A massa específica e o calor específico da folha são e , enquanto as propriedades do ar podem ser consideradas iguais a , , .
- Levando em conta os efeitos da radiação, com e , integre numericamente a equação diferencial deduzida na parte (a) e determine a temperatura da folha em . Estude o efeito de na distribuição de temperaturas ao longo da folha.
Passo 1
O grande trabalho desta questão é encontrar a equação diferencial que governa o nosso problema. Para encontrarmos esta equação, precisaremos fazer um balanço de energia.
Neste caso, como vamos partir de elementos diferenciais, ajuda bastante fazermos um simples esboço, como o esboço abaixo, para ajudar a gente na hora de elaborar os termos. Então,
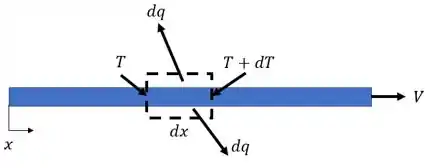
Vamos considerar o nosso volume de controle parado. Isto implica em dizer que estamos em regime permanente, pois não há acumulo de calor no elemento. Como também não há termo de geração de calor, temos o seguinte balanço:
Passo 2
Agora, quem é o termo que entre e quem é o que sai? O termo que entre é a energia do elemento na posição . Este termo é:
E qual é o termo que sai, que está na posição ? É devido a ação da convecção, da radiação e também a parte devido a energia do elemento. Então, temos:
Detalhe para o . É multiplicado por 2 pois temos duas superfícies, e ele engloba o termo de convecção e radiação. Continuando,
Portanto, o nosso balanço de energia é:
E esta é nossa equação diferencial, respondendo a letra a).
OBS: vocês podem ter estranhado os termos de energia do elemento e achados eles bastante semelhantes ao termo de acúmulo de energia. E sim, estão corretos.
Só que nós só podemos considerar eles como termo de acúmulo se estivermos em regime transiente. E para que isto ocorra, o nosso volume de controle deve se mover com a folha. Neste caso só teríamos o termo de saída devido a convecção e radiação, e o termo de acúmulo.
Passo 3
Agora vamos resolver a letra b). Para isto, precisamos resolver a equação diferencial, desconsiderando a parte da radiação. Portanto, temos:
Para obtermos uma solução fechada para a equação diferencial acima, vamos integrar do ponto inicial e até o ponto final e , temos:
Fizemos isto para que o segundo membro seja exatamente o coeficiente médio de transferência de calor. Então, temos:
E assim obtemos uma solução fechada.
Passo 4
Para finalizarmos a letra b), precisamos substituir os valores das constantes. Entretanto, nos falta o coeficiente de transferência de calor médio. Então, vamos obtê-lo primeiramente.
Como estamos em regime turbulento (a questão informou), basta aplicarmos a seguinte relação
Calculando o número de Reynolds, temos:
Portanto, o coeficiente de transferência de calor médio é:
Portanto, a temperatura será obtida quando na seguinte equação:
E assim acabamos de resolver a letra b)
Passo 5
Para resolvermos a letra c), vamos precisar de algum auxílio computacional para poder resolver a integral.
Mas será se realmente precisa disto tudo? E qual o motivo?
Bom... lembra no início da letra b) (Passo3) que dizemos para desconsiderar o termo de radiação e integrar? Pois é, vamos ter que considerar agora. Então, temos que resolver a seguinte equação diferencial:
Com todos os valores das constantes que usamos no Passo 4, mais o termo , e (não esqueça que sempre que trabalhamos com radiação, temos que colocar a temperatura em Kelvin!).
Agora fica fácil ver que é uma integral bastante difícil de ser resolvida, não é? Então, se resolvermos numericamente, vamos obter o seguinte valor para a temperatura: