Repita o Problema para o caso mais geral. Isto é, o cilindro interno girando a uma velocidade angular e o cilindro externo girando a uma velocidade angular . Tudo o mais permanece o mesmo que o Problema . Gere uma expressão exata para a componente da velocidade, como uma função do raio e dos outros parâmetros do Problema. Verifique se quando o seu resultado se simplifica para o do Problema .

Como primeiro passo, vamos desenhar nosso eixo de coordenadas:

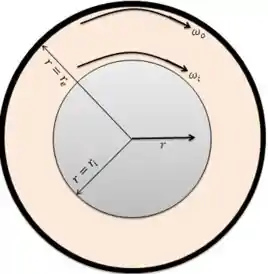
Nosso próximo passo para obter o perfil será aplicar a equação da continuidade para coordenadas cilíndricas:

Assumindo que estamos em regime estacionário e que as componentes de velocidade nas direções e são nulas:

Então, nossa equação se reduz à:

Ou seja, pela equação da continuidade concluímos que a velocidade não depende da componente . O que é equivalente a dizer:

Tudo bem até aqui?

Nosso próximo passo será aplicar a equação de Navier-Stokes. Vamos lá?

Como o fluido está “escoando” apenas na direção , vamos aplicar a equação de Navier-Stokes para esta componente:

Vamos analisar os termos do lado esquerdo da equação. Consideramos que o sistema está em regime estacionário, além de que e . Também vimos pela equação da continuidade que . Então, o lado esquerdo da equação fica:

Vamos olhar agora os termos do lado direito. O fluido está escoando apenas devido à movimentação dos cilindros, sem a ação de gradiente de pressão ou da força gravitacional. Então:

Como só temos velocidade na direção :

Além disso, pela equação da continuidade vimos que , portanto

E a equação de Navier-Stokes é reduzida à:

Como a derivada em relação à zero, podemos dizer que

Em que é uma constante. Continuando:

Integrando os dois lados da equação:

Para encontrar as constantes, vamos agora aplicar as condições de contorno. As condições de contorno são as seguintes:

Então, substituindo no perfil:

E

Substituindo as constantes no perfil teremos:

Por fim, vamos ver se chegamos no mesmo resultado do Problema , em que .

Se aplicarmos no perfil de velocidades ficamos com:

Se fizermos :

O perfil atendeu à primeira condição de contorno (). Vamos agora verificar se :

Mostramos então, que o nosso perfil geral é equivalente ao obtido no Problema .