Radiação entre Superfícies
Produzido por Giovanna RonzéTeoria
Introdução
Até aqui já sabemos como trabalhar com problemas de radiação entre superfícies negras, mas no mundo real, o que a gente encontra são superfícies não negras, onde ocorrem múltiplas reflexões... o que a gente faz nesse caso?
Por exemplo: Duas esferas concêntricas de diâmetros e são mantidas a temperaturas uniformes e e têm emissividades e .
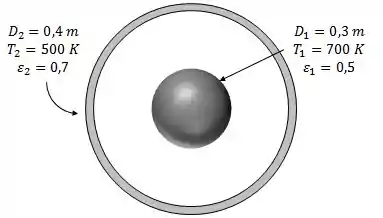
Nesse caso, qual é a taxa de transferência de calor por radiação entre as duas esferas?
Analisar a radiação nesse tipo de situação não é uma tarefa fácil, então precisamos fazer algumas simplificações pra facilitar a nossa vida. Dessa forma, consideramos que as superfícies são:
- Opacas: A transmissividade é nula;
- Difusas: Elas emitem e refletem a radiação igualmente em todas as direções;
- Cinzas: Suas propriedades independem do comprimento de onda da radiação;
- Isotérmicas uniformes: A temperatura nas superfícies são constantes e estão uniformemente distribuídas.
Antes de entender como essas superfícies trocam calor, precisamos entender primeiro como uma superfície troca calor por radiação.
Transferência de Calor a partir de uma Superfície
A taxa de transferência de calor por radiação em uma superfície é a diferença entre o que sai e o que entra :
![]()
Onde é a irradiação, e é a radiosidade, definida como a energia total de radiação que deixa uma superfície por unidade de tempo e por unidade de área.
Quando uma superfície está na presença de radiação emitida por outros corpos, a radiação total que deixa essa superfície é constituída pela radiação emitida pela mesma e pela radiação refletida pela mesma . Logo:
![]()
Juntando essas duas equações, podemos escrever a taxa de transferência de calor por radiação a partir de uma superfície como:
Onde é a resistência da superfície à radiação, dada por:
![]()
Até aqui, tudo muito lindo, mas o que acontece quando temos outras superfícies no problema?
Transferência de Calor entre Superfícies
Nesse caso a taxa líquida de transferência de calor do corpo 1 para o corpo 2 será igual a:
Ou seja, ela será igual à diferença entre o quanto o corpo 1 emite para o corpo 2 e o quanto 2 emite para o corpo 1. Se aplicarmos a regra da reciprocidade do Fator de forma e reorganizar os termos da equação, encontraremos o seguinte:
![]()
Onde é a resistência de espaço à radiação, dada por:
![]()
“Mas e se não soubermos calcular a radiosidade?”
Opa! A pergunta é muito boa! Nesse caso, podemos trabalhar com as duas superfícies como se fossem negras, mas o preço que temos que pagar é adicionar as resistências de superfície das duas superfícies. A ideia é a seguinte:
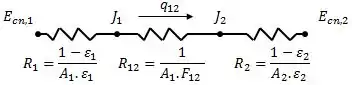
Logo:
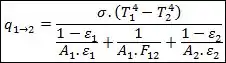
Opa! Com isso aqui já podemos calcular a taxa de transferência de calor pra resolver no nosso problema. Mas, para o nosso problema, tem um jeito mais fácil!
Transferência de Calor em Recintos com duas Superfícies
Alguns casos, como o nosso, temos expressões tabeladas pra taxa de transferência de calor. Não é sempre que isso vai acontecer, então nem pense em ignorar tudo o que vimos até aqui. ;)
Se liga:

Voltando ao nosso problema...
Olhando na tabela, temos uma equação exata pra resolver a nossa vida, dada por:
Onde , logo:
![]()
Escudos de Radiação
Como o nome sugere, o objetivo dos escudos de radiação é reduzir a transferência de calor. Isso acontece se colocarmos placas, ou cascas de baixa emissividade entre duas superfícies.
A ideia é a seguinte:
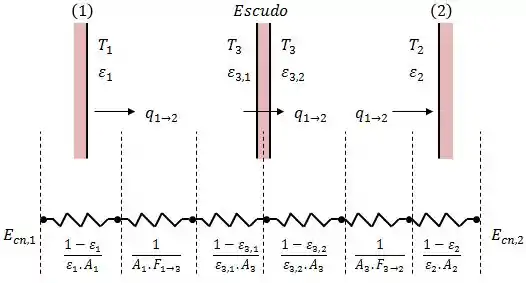
Conforme a nossa tabela, sem o escudo de radiação:
Agora, ao colocarmos o escudo de radiação, a taxa de transferência passa a ser dada por:
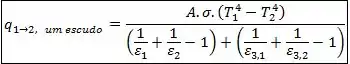
Se tivermos escudos, vamos somando a contribuição de cada um no denominador:
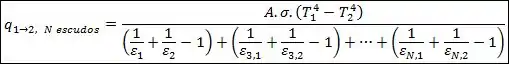
Se todas as superfícies tiverem a mesma emissividade, a equação acima pode ser escrita como:
![]()
Estamos prontos pra cair nos exercícios!
Transferência de Calor a partir de uma Superfície
Transferência de Calor entre Superfícies
Transferência de Calor em Recintos com duas Superfícies
Voltando ao nosso problema...
Escudos de Radiação
Exercícios Resolvidos
Exercício Resolvido #1
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Considere duas placas paralelas muito grandes com superfícies cinza e difusas.
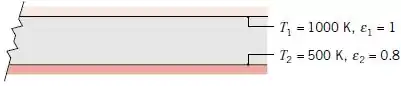
Determine a irradiação na placa superior.
Determine a radiosidade na placa superior.
Qual é a radiosidade da placa inferior.
Qual é a troca líquida de radiação entre as placas por unidade de área das placas?
Passo 1
Determine a irradiação na placa superior.
Sobre a placa superior incide a radiaç��o vinda da placa inferior, e a radiação emitida pela placa superior e que foi refletida pela placa inferior.
Dessa forma:
Substituindo os valores:
![]()
Passo 2
Determine a radiosidade na placa superior.
A radiosidade é definida por
Como a placa superior se trata de um corpo negro, , nenhuma radiação será refletida. Dessa forma:
![]()
Passo 3
Qual é a radiosidade da placa inferior.
No caso da placa inferior, teremos:
A irradiação será composta somente da energia que vem da placa superior, já que a mesma não irá refletir a radiação emitida pela placa inferior. Logo:
![]()
Passo 4
Qual é a troca líquida de radiação entre as placas por unidade de área das placas?
A troca líquida entre as placas pode ser calculada da seguinte forma:
![]()
A mesma ainda poderia ser calculada da seguinte forma:
Resposta
Exercício Resolvido #2
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
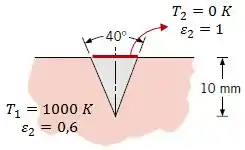
Considere uma longa fenda em forma de com profundidade de , usinada em um bloco mantida a .
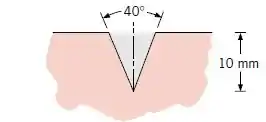
Se as superfícies da fenda são difusas e cinza com uma emissividade de , determine o fluxo radiante que deixa a fenda para a sua vizinhança. Determine também a emissividade efetiva da cavidade.
Passo 1
Uma boa estratégia pra esse tipo de problema é “fechar” a superfície.
Assim, como nós queremos calcular o fluxo radiante que deixa a fenda, vamos idealizar uma superfície que feche a fenda, onde essa superfície é um corpo negro com temperatura . Ou seja, essa superfície irá absorver todo o fluxo de energia.
Fazendo isso e calculando o fluxo térmico entre a fenda e a nossa superfície, vamos estar calculando o fluxo radiante que deixa a fenda.
Passo 2
A taxa de radiação emitida pela superfície será dada por:
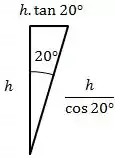
O fator de forma pode ser calculado através da seguinte relação:
Como a superfície que inventamos é plana, qualquer radiação que ela pudesse emitir jamais incidiria sobre ela mesma, logo:
Pela regra da adição:
Assim:
Como queremos calcular o fluxo radiante, basta dividir toda a expressão pela área que inventamos, logo:
Além disso, como a superfície 2 é negra, , logo:
Passo 3
Em relação às áreas, temos o seguinte:
Assim, substituindo os valores:
![]()
Resposta
Exercício Resolvido #3
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Para melhorar o descarte de calor em espaçonaves, um engenheiro propõe fixar uma série de aletas retangulares à superfície externa da espaçonave e cobrir todas as superfícies com um material que se aproxima de um comportamento de corpo negro.
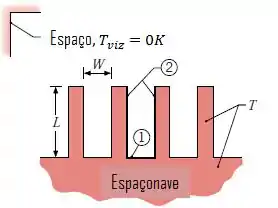
Para superfícies isotérmicas com temperaturas e emissividade , e uma seção em com largura e comprimento , determine a taxa, por unidade de comprimento (normal à página), na qual radiação é transferida de uma seção para o espaço.
Passo 1
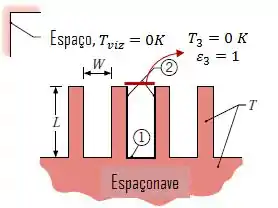
A boa pra esse tipo de problema é “fechar” a cavidade.
Assim, vamos imaginar uma superfície que feche a fenda, onde essa superfície é um corpo negro com temperatura , de forma que essa superfície absorva todo o fluxo de energia.
Fazendo isso e calculando o fluxo térmico entre a cavidade e a nossa superfície, vamos estar calculando o fluxo radiante que a deixa.
Passo 2
A taxa de radiação que incide na superfície 3 será dada por:
Onde:
Em que é o comprimento da cavidade (na direção normal à página).
Como a superfície que inventamos é plana, nenhuma radiação que ela pudesse emitir incidiria sobre ela mesma, logo:
Pela regra da adição:
Pela regra da reciprocidade:
![]()
Passo 3
Assim:
Como queremos calcular a taxa de transferência de calor por unidade de comprimento, basta dividir toda a equação pelo comprimento , logo:
Além disso, como a superfície 3 é negra, , logo:
Passo 4
Substituindo os valores:
![]()
Resposta
Exercício Resolvido #4
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Um condutor elétrico muito longo, com de diâmetro, está posicionado concentricamente no interior de um tubo cilíndrico resfriado, com de diâmetro, cuja superfície é difusa e cinza com uma emissividade de e está à temperatura de .
O condutor elétrico possui uma superfície difusa e cinza com uma emissividade de e está dissipando por metro de comprimento.
Considerando que há vácuo no espaço entre as duas superfícies, calcule a temperatura na superfície do condutor.
Passo 1
A taxa de transferência de calor no caso de cilindros concêntricos e infinitamente grandes é dada por:
Onde . Como o problema nos deu a taxa de transferência de calor por unidade de comprimento, basta dividir toda a expressão por , logo:
Passo 2
Reorganizando os termos da expressão que encontramos no Passo 1 pra isolar a temperatura , teremos:
Substituindo os valores:
Jogando isso tudo na calculadora, vamos encontrar o seguinte:
![]()
Resposta
Exercício Resolvido #5
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Oxigênio líquido é armazenado em um vaso esférico com parede delgada e de diâmetro, que está encerrado no interior de um segundo vaso esférico, também com parede delgada e com de diâmetro.
As superfícies dos vasos são cinza, difusas e opacas, com uma emissividade de e são separadas por um espaço no qual há vácuo.
Se a superfície externa está a e a superfície interna está a , qual é a taxa mássica de perda de oxigênio devido à evaporação?
Obs.: O calor latente de vaporização do oxigênio é de .
Passo 1
A taxa de transferência de calor para esferas concêntricas é dada por:
Essa mesma taxa de transferência de calor está sendo utilizada para a vaporização do oxigênio, logo:
Onde . Assim a vazão mássica será dada por:
Passo 2
Substituindo os valores:
![]()
Resposta
Exercício Resolvido #6
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Considere duas grandes superfícies paralelas, cinza e difusas, separadas por uma pequena distância.
Se a emissividade das superfícies é de , qual deve ser a emissividade de uma barreira de radiação delgada para reduzir a taxa de transferência de calor por radiação entre as duas superfícies por um fator de 10?
Passo 1
Pra poder comparar esses caras, vamos encontrar as expressões para as taxas de transferência de calor por radiação com e sem a barreira .
A taxa de transferência de calor entre placas infinitamente grandes é dada por:
Com o escudo, a taxa de transferência de calor passa a ser dada por:
Passo 2
A relação entre as duas transferências de calor deve ser tal que:
Reorganizando os termos, teremos:
Substituindo os valores:
Agora é arrumar a bagunça:
![]()
Resposta
Exercício Resolvido #7
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
No fundo de uma grande câmara de vácuo cujas paredes estão a , um painel negro com de diâmetro é mantido a .
Para reduzir o calor ganho nesse painel, uma barreira de radiação com o mesmo diâmetro e uma emissividade de é colocada muito próximo ao painel.
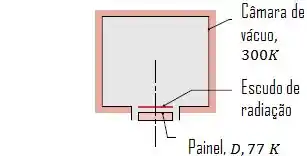
Calcule o ganho líquido de calor no painel.
Passo 1
A taxa de transferência de calor será dada por:
Contabilizando todas as resistências à radiação do sistema, temos o seguinte:

Passo 2
Como ou , a primeira resistência à radiação será aproximadamente nula. Além disso, como a placa é uma superfície negra, , zerando a última resistência à radiação.
Dessa forma:
Onde:
![]()
Logo:
Arrumando a bagunça:
Passo 3
Assim, a taxa de transferência de calor será dada por:
Onde .
Dessa forma:
![]()
Resposta
Exercício Resolvido #8
INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.
Uma barreira de radiação difusa e cinza, com de diâmetro e emissividade e nas superfícies interna e externa, respectivamente, é concêntrica a um longo tubo que transporta um fluido de processo quente.
A superfície do tubo é negra e possui diâmetro de . Há vácuo na região interna da barreira. A superfície externa da barreira está exposta a uma grande sala, cujas paredes estão a , e experimenta transferência de calor por convecção com o ar a , com um coeficiente convectivo de .
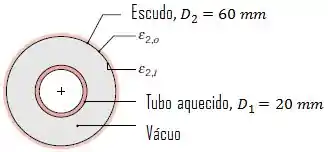
Determine a temperatura de operação do tubo interno se a temperatura da barreira for mantida a .
Passo 1
Fazendo o balando de energia na superfície externa, temos que:
Passo 2
A taxa de transferência de calor entre as superfícies cilíndricas é dada pela seguinte equação tabelada:
A taxa de transferência de calor por convecção será dada por:
A taxa de transferência de calor por radiação entre o tubo externo e a vizinhança será dada por:
Substituindo esses caras na equação que encontramos no Passo 1:
Passo 3
Colocando ordem na casa e isolando a temperatura , teremos:
Substituindo os valores e jogando isso tudo na calculadora, vamos encontrar:
![]()
Resposta
Exercício Resolvido #9
Questão 3, PUC, P3-2006
A parede de um forno industrial é composta por duas paredes planas verticais distantes e com ar (a ) entre elas. As paredes têm altura igual a e largura igual a . A temperatura da parede 1 é mantida a , e a da parede 2 é mantida a .
A emissividade da parede 1 é igual a e a da parede 2, . Considere as paredes como superfícies cinzas difusas e calcule:
O coeficiente de troca de calor por convecção na parede 1, assumindo que a parede 2 não perturba o escoamento próximo a parede 1.
O calor total perdido pela parede 1.
Considere as seguintes propriedades para o ar: .
Passo 1
O coeficiente de troca de calor por convecção na parede 1, assumindo que a parede 2 não perturba o escoamento próximo a parede 1.
Esse se trata de um problema de convecção natural. Sendo assim, o número de Rayleigh será dado por:
O número de Rayleigh é dado por:
Onde vale:
Assim, substituindo os valores:
Passo 2
Como estamos trabalhando com um caso de placa vertical, para o valor de número de Rayleigh que encontramos, a correlação mais adequada para o número de Reynolds é dada por:
O coeficiente convectivo será:
![]()
Passo 3
O calor total perdido pela parede 1.
O calor total perdido pela parede 1 será a soma do calor perdido por convecção e do calor perdido por radiação . Dessa forma:
Passo 4
O calor perdido por radiação pode ser calculado por:
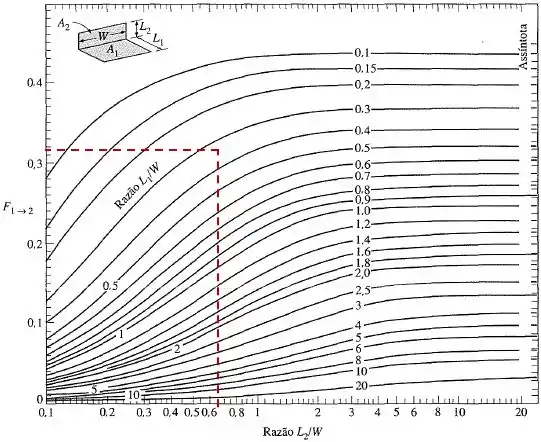
Onde o fator de forma é obtido a partir do gráfico abaixo, onde:
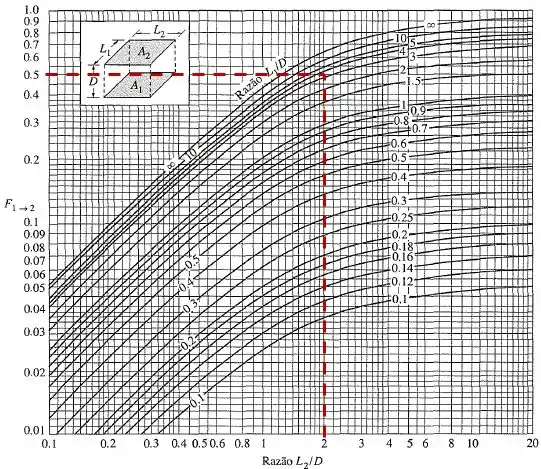
Dessa forma, sendo e :
Assim, o calor perdido pela placa 1 será:
![]()
Resposta
Exercício Resolvido #10
Questão 2, UFF, P2-2017.2
Uma pirâmide tradicional (base quadrada) é utilizada para aquecer objetos colocada no centro da placa da base. As faces triangulares da pirâmide estão a e a base está a .
Qual a quantidade de calor trocada entre a pirâmide e a sua base, considerando apenas a radiação térmica e que as superfícies possuem, respectivamente, emissividade térmica de e ? A base da pirâmide é quadrada com 1,4 metros em cada lado e a altura é de 2,5 metros.
Passo 1
A taxa de transferência de calor entre cada lado da pirâmide e a base é dada por:
De forma que a quantidade de calor total trocada será:
Dessa equação, temos quase tudo, mas precisamos calcular o fator de forma e as áreas das superfícies.
Passo 2
Vamos começar pelo fator de forma.
Devido à simetria do sistema, podemos dizer que:
Além disso, pela regra da adição:
Pela regra da reciprocidade:
A área da base é dada por:
A área do lado triangular é dada por:
Onde é a altura do lado triangular, dada por:
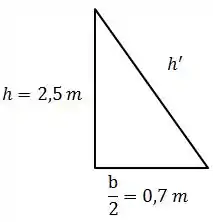
Assim, o fator de forma será:
Passo 3
Assim, a taxa de transferência de calor será:
![]()
Resposta
Exercício Resolvido #11
Questão 2, UFF, P2-2016.2
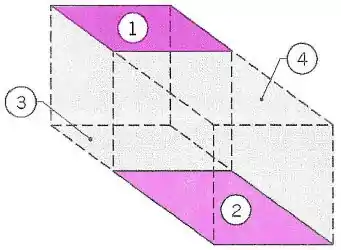
(Adaptado) Uma sala de de lado contém duas placas identificadas como 1 e 2 na figura abaixo.
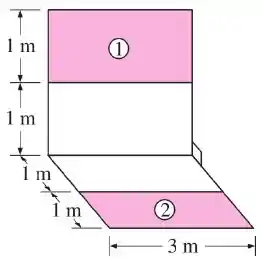
As demais faces da sala são reirradiantes. Sabendo que a placa 1 está a e emite radiação como um corpo negro e que a placa 2 está a e é um corpo cinza e difuso que possui uma emissividade de , determine:
provando matematicamente, quais os fatores de forma associados ao sistema.
o fluxo de calor radiante entre as placas 1 e 2.
Passo 1
Determine, quais os fatores de forma associados ao sistema.
A ideia aqui é a seguinte: vamos completar a parede da seguinte forma.
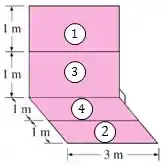
Onde queremos determinar os fatores de forma e . Os dois estão relacionados pela regra da reciprocidade, dada por:
Como :
Passo 2
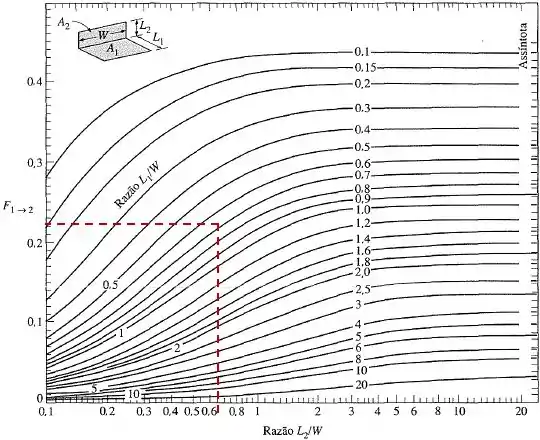
Utilizando os gráficos, podemos determinar os fatores de forma e .
Dessa forma, para o primeiro caso, teremos:
Para o segundo caso:
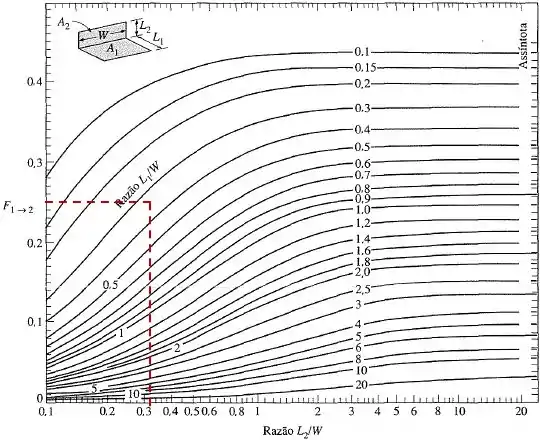
Passo 3
Através da regra da superposição, temos que:
Dessa equação, precisamos dos fatores de forma e . No entanto, devido à regra da simetria, podemos afirmar que:
Assim, teremos o seguinte:
Onde, para o fator de forma , teremos:
Logo:
Passo 4
Finalmente, o fator de forma será:
Onde . Logo:
![]()
Passo 5
Determine o fluxo de calor radiante entre as placas 1 e 2.
O fluxo de calor é dado por:
Onde:
Assim:
![]()
Resposta
Exercício Resolvido #12
Questão 4, UFF, P2-2017.1
Caracterize analiticamente, provando suas conclusões passo-a-passo, o fator de forma entre a superfície 1 e 2, escrevendo esse fator de forma em função de fatores elementares de forma que esses possam ser encontrados em figuras ou tabelas.
Determine também qual a transferência de calor entre 1 e 2, assumindo que em 1 a temperatura seja de e em 2 a temperatura seja de , sabendo que ambas as superfícies são aço inoxidável, típico, polido. Sabendo também que o meio interno a essa superfície é composto por vácuo.
Passo 1
Usando a regra da superposição, podemos dizer que:
Passo 2
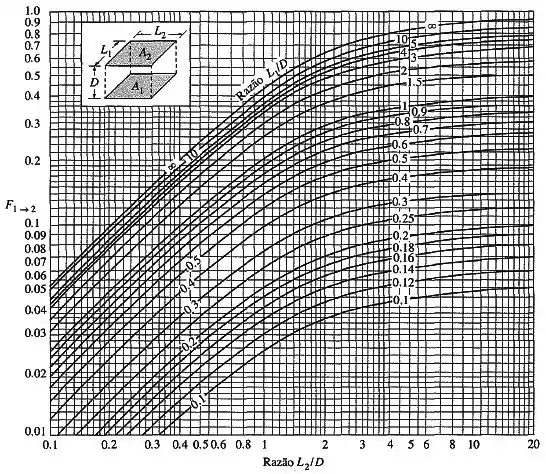
Os fatores de forma , e podem ser encontrados pelo gráfico abaixo:
Passo 3
Para calcular o fator de forma , ainda precisamos lidar com o fator de forma .
Pela regra da simetria:
E, pela regra da reciprocidade:
Onde . Dessa forma:
Logo:
Substituindo na expressão que encontramos no Passo 1:
Agora é só uma questão de arrumar a bagunça:
![]()
Passo 4
Como o problema não nos deu a emissividade das superfíciesA transferência de calor será dada por:
Para calcular o fator de forma , temos que, considerando cada superfície quadrada e que a distância entre as superfícies é igual ao lado de cada uma delas:
Assim:
Passo 5
A taxa de transferência de calor será:
De acordo com a tabela A.11 do Incropera, para aços inoxidáveis, típicos e polidos:
Dessa forma, considerando :
Como não temos o valor de :
O sinal negativo se dá pelo fato de que, como a superfície 1 possui uma temperatura menor que a superfície 2, o calor na verdade flui de 2 para 1. Logo:
![]()
Resposta
Exercício Resolvido #13
Questão 3, UFF, P2-2016.1
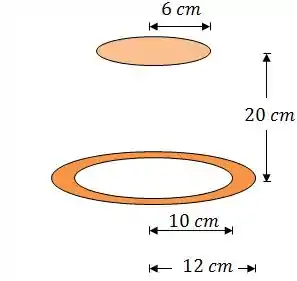
(Adaptado) Um anel com de raio interno e de raio externo é uma peça de aquecimento por radiação de um plano em formato de disco de de raio paralelo ao anel a uma distância de .
Toda uma região que fecha o sistema (forma uma cavidade fechada) é formada de um material que isola o sistema, ou seja, por uma superfície reirradiante.
Sabendo que o anel está a e emite radiação como um corpo negro e que o disco inferior está a e é um corpo cinza e difuso que possui uma emissividade de , determine qual o fluxo de calor radiante entre o disco e o anel.
Passo 1
A taxa de transferência de calor entre as duas superfícies é dada por:
Graficamente, a ideia é essa:
Da equação da taxa de transferência de calor, o único termo que nos resta calcular é o fator de forma.
Passo 2
Pra calcular o fator de forma, vamos criar uma superfície imaginária da seguinte forma:
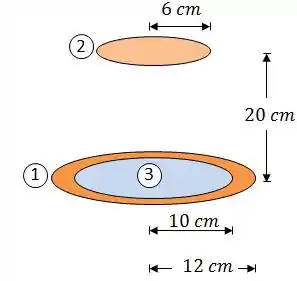
De forma que, pela regra da superposição:
Os fatores de forma e podem ser calculados a partir do gráfico abaixo.
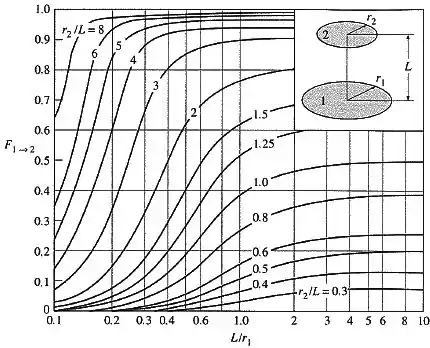
Onde, para :
E, para :
Assim:
Dessa forma, o fator de forma será:
Passo 3
A taxa de transferência de calor será:
Como o anel emite radiação como corpo negro , podemos reescrever a equação acima como:
Substituindo os valores:
![]()
Resposta
Exercício Resolvido #14
Questão 3, UFF, P2-2015.1
Considere uma sala de 2 metros de altura e uma base quadrada de de lado. Um quadro formado por uma placa aquecedora (A) quadrada de de lado está com sua base a do chão pendurado na parede.
No chão, foi instalada outra placa aquecedora (B) também quadrada de de lado. Todas as demais faces expostas da sala são rerradiantes e forma-se uma cavidade fechada com vácuo no seu interior.
Sabendo que a placa aquecedora (A) tem uma emissividade igual a da placa (B), sendo o valor igual a 0, 4 e considerando que a placa (A) está a e a placa (B) a , determine a taxa de troca de calor entre as placas (A) e (B)
Passo 1
A taxa de transferência entre as placas será dada por:
Dessa equação, precisamos somente do fator de forma .
Passo 2
A ideia aqui é basicamente essa:
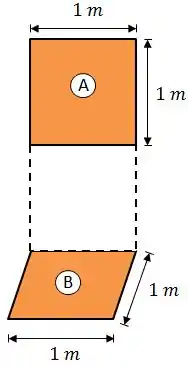
Para calcular o fator de forma, entre e , vamos inventar uma terceira superfície :
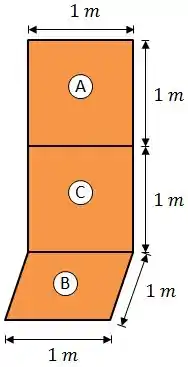
De forma que:
Os fatores de forma podem ser calculados partir de gráficos, onde:
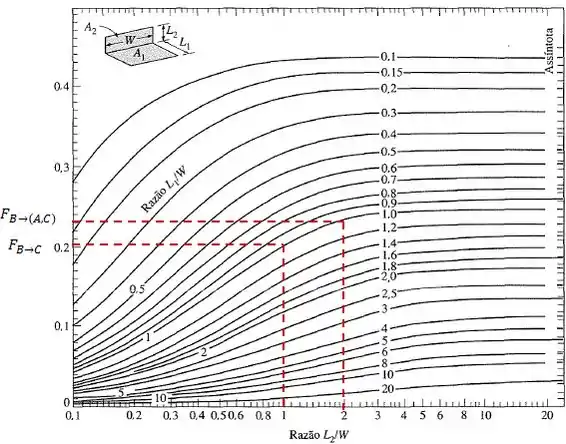
Dessa forma, o fator de forma será:
Passo 3
A taxa de transferência de calor será:
![]()
Resposta
Exercício Resolvido #15
Questão 3, UFRJ, P2-2015.2
Em uma plataforma espacial, duas placas de mesmo tamanho são paralelas e estão separadas de . Uma das placas está na temperatura de e a outra na temperatura de .
Essas placas não sofrem incidência solar e o ambiente ao seu redor encontra-se na temperatura de . Para a troca de calor por radiação, o ambiente pode ser representado como uma superfície fictícia, unindo as duas placas e formando a cavidade na forma de um paralelepípedo que é mostrada abaixo.
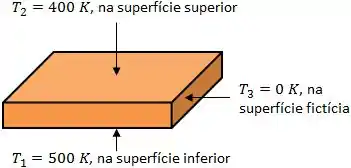
Todas as superfícies são negras. Qual o fluxo de calor por radiação em cada uma das superfícies?
Passo 1
O fluxo de calor em cada superfície é dada por:
Onde as radiosidade são dados por:
Agora temos que descobrir os fatores de forma.
Passo 2
Como as superfícies 1 e 2 são planas:
![]()
O fator de forma entre as superfícies 1 e 2 é dado pelo gráfico abaixo:
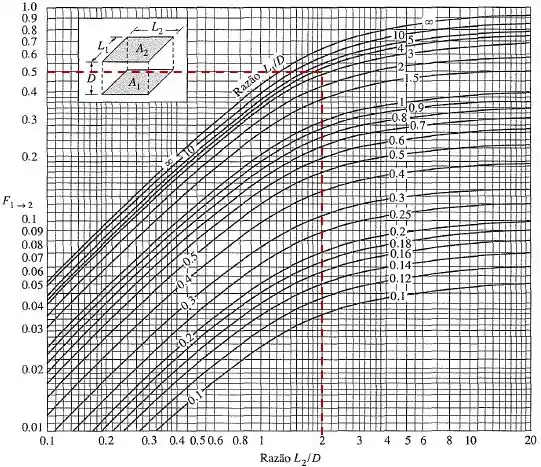
![]()
Utilizando a regra da adição:
![]()
Através da regra da reciprocidade, onde:
Teremos:
![]()
Pela regra da adição:
![]()
Passo 3
Finalmente, os fluxos de calor em cada superfície serão:
![]()
![]()
![]()