Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Propriedades Radioativas

Ver Todos os Exercícios

Teoria

Introdução

Sabe quando você está dormindo de boa e alguém decide acordá-lo sutilmente escancarando a cortina do seu quarto?

Porque a radiação solar chega tão mais intensa em você quando passa através do vidro da janela, do que quando incide somente sobre a cortina?!

Isso acontece porque os materiais podem emitir, absorver, refletir ou transmitir a radiação de maneiras distintas. E estamos justamente interessados nas propriedades que nos dirão como se comportam os materiais em relação à radiação.

Do que dependem essas propriedades?

As propriedades que veremos dependem não só do comprimento de onda da radiação, mas também da direção com que essa radiação está sendo emitida, ou recebida.

Como essa dependência complica um pouco a análise da radiação em alguns casos, vamos considerar, na maioria dos casos que veremos, superfícies cinza e difusas.

Bom, uma superfície cinza é aquela em que as suas propriedades independem do comprimento de onda da radiação. E uma superfície difusa é aquela em que as suas propriedades são constantes em qualquer direção.

Quando estudamos o corpo negro anteriormente, vimos que ele é um perfeito emissor e absorvedor de radiação. Além disso, dissemos que nenhum corpo emite mais radiação do que um corpo negro a uma mesma temperatura.

Então a ideia é usar esse cara como referência na hora de tratar dessas propriedades radioativas dos materiais.

Já está na hora de sermos devidamente apresentados.

Emissividade ε

A emissividade média é a razão entre a radiação emitida por uma superfície a uma temperatura T s e a radiação emitida por um corpo negro na mesma temperatura T s , ou seja:

Assim, em boa parte dos casos, a potência emissiva de uma superfície a temperatura T s pode ser calculada por:

Agora, como nem tudo são flores, o problema pode te fornecer valores de emissividade que são constantes em determinados valores de comprimento de onda, por exemplo:

ε = ε 1 ,         0 ≤ λ < λ 1 ε 2 ,         λ 1 ≤ λ < λ 2 ε 3 ,         λ 2 ≤ λ < ∞

Nesse caso, a emissividade pode ser calculada da seguinte forma:

Onde f λ 1 → λ 2 é a função de radiação do corpo negro, que possui os seguintes valores tabelados:

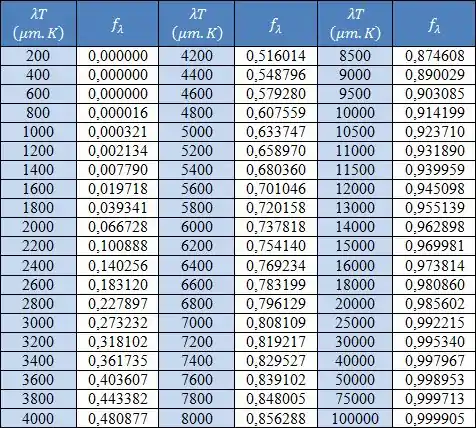
Absortividade α , refletividade ρ e transmissividade τ

A ideia aqui é muito parecida com a emissividade. A diferença é que essas propriedades não estão associadas à radiação emitida por um corpo, mas sim à radiação que incide sobre um corpo, chamada irradiação G .

Assim, a absortividade α é definida como sendo a fração da irradiação que é absorvida pelo corpo:

Na prática, a gente considera a absortividade como sendo igual à emissividade, logo:

Ou seja, se temos um corpo com uma temperatura superficial T s e uma vizinhança com temperatura T v i z , sendo T v i z < T s , o fluxo térmico por radiação no corpo é dado por:

q r a d ' ' = ε . σ . T s 4 - α . σ . T v i z 4

Que nada mais é a diferença entre o que ele emite e o que ele recebe de calor.

A refletividade ρ é definida como sendo a fração da irradiação que é refletida pelo corpo:

Em boa parte dos casos, considera-se que as superfícies apresentam reflexão especular (tipo um espelho, geralmente considerada em superfícies polidas), ou reflexão difusa (em todas as direções, geralmente considerada em superfícies rugosas).

Por fim, a transmissividade τ corresponde à fração da irradiação que é transmitida pelo corpo:

Toda vez que o problema falar de um corpo opaco, ele basicamente está nos falando pra considerar a transmissividade nula τ = 0 .

A ideia é basicamente a seguinte:

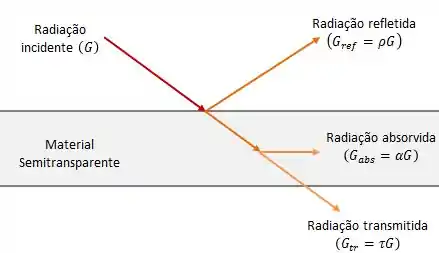
Dessa forma, a soma das porções absorvida, refletida e transmitida pelo corpo deve ser igual à irradiação sobre ele:

G a b s + G r e f + G t r = G

Logo:

Vamos pensar na seguinte situação...

A emissividade de um corpo opaco pode ser aproximada como 0,5 para a radiação em comprimentos de onda menores de 1   μ m e 0,15 para radiação superior a 1   μ m .

Qual seria a emissividade média desse corpo a 2000   K ? Além disso, qual seria a absortividade e a refletividade?

Opa! Como a emissividade está associada a um intervalo de comprimentos de onda, podemos calculá-la da seguinte forma:

ε T = ε 1 . f 0 → λ 1 T + ε 2 . f λ 1 → ∞ T

Já podemos trabalhar nessa equação, se liga:

ε = ε 1 . f λ 1 - f 0 + ε 2 . f ∞ - f λ 1

ε = ε 1 . f λ 1 - 0 + ε 2 . 1 - f λ 1

ε = ε 1 . f λ 1 + ε 2 . 1 - f λ 1

Onde:

ε 1 = 0,5

ε 2 = 0,15

λ 1 = 1   μ m

Dessa forma, temos que:

λ 1 . T = 1 × 2000 = 2000   μ m . K

Olhando na tabela da função de radiação do corpo negro, temos que f λ 1 = 0,066728 , logo:

ε = ε 1 . f λ 1 + ε 2 . 1 - f λ 1

ε = 0,5 × 0,066728 + 0,15 × 1 - 0066728

Agora que encontramos a emissividade, a absortividade será:

α = ε

Para calculara refletividade, vamos utilizar a seguinte equação:

α + ρ + τ = 1

Como estamos trabalhando com um corpo opaco, τ = 0 , logo:

α + ρ = 1

ρ = 1 - α = 1 - 0,173

Agora estamos prontos pra cair dentro nos exercícios. :)

Emissividade ε

Absortividade α , refletividade ρ e transmissividade τ

Vamos pensar na seguinte situação...

Exercícios Resolvidos

Exercício Resolvido #1

ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.

A função emissividade espectral de uma superfície opaca a 1000   K é aproximada como:

ε i = ε 1 = 0,4 ,                                 0 ≤ λ < 2   μ m ε 2 = 0 , 7 ,     2   μ m ≤ λ < 6   μ m ε 3 = 0 , 3 ,                                 6   μ m ≤ λ < ∞

Determinar a emissividade média da superfície e a taxa de emissão de radiação na superfície, em W / m 2 .

Passo 1

A emissividade média será dada por:

ε = ε 1 . f 0 → λ 1 + ε 2 . f λ 1 → λ 2 + ε 3 . f λ 2 → ∞

ε = ε 1 × f λ 1 - 0 + ε 2 × f λ 2 - f λ 1 + ε 3 1 - f λ 2

Passo 2

As funções de radiação do corpo negro a 1000   K serão:

λ 1 . T = 2 × 1000 = 2000   μ m . K → f λ 1 = 0,066728

λ 2 . T = 6 × 1000 = 6 000   μ m . K → f λ 2 = 0 , 737818

Dessa forma, a emissividade média será:

ε = ε 1 × f λ 1 + ε 2 × f λ 2 - f λ 1 + ε 3 1 - f λ 2

ε = 0,4 × 0,066728 + 0,7 × 0,737818 - 0,066728 + 0,3 1 - 0,737818

Passo 3

A taxa de emissão de radiação da superfície será:

E = ε . σ . T 4 = 0,575 × 5,67 × 10 - 8 × 1000 4

Resposta

ε = 0,575

E = 32,6   k W / m 2

Exercício Resolvido #2

ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.

Um forno que tem uma janela de vidro de 40   c m × 40   c m pode ser considerado um corpo negro a 1200   K .

Se a transmissividade do vidro é de 0,7 para a radiação em comprimentos de onda inferiores a 3   μ m e zero para a radiação em comprimentos de onda superiores a 3   μ m , determinar a fração e a taxa de radiação proveniente do forno e transmitida através da janela.

Passo 1

A fração da radiação transmitida é justamente o conceito de transmissividade.

A transmissividade média pode ser calculada da seguinte forma:

τ = τ 1 . f 0 → λ 1 + τ 2 . f λ 1 → ∞

τ = τ 1 . f λ 1 - 0 + τ 2 . 1 - f λ 1

Passo 2

A função de radiação do corpo negro será:

λ 1 . T = 3 . 1200 = 3600   μ m . K → f λ 1 = 0,403607

Assim, a transmissividade média será:

τ = τ 1 . f λ 1 + τ 2 . 1 - f λ 1

τ = 0,7 . 0,403607 + 0 . 1 - 0,403607

Passo 3

A taxa de radiação proveniente do forno e transmitida através da janela será dada por:

G t r = τ . A . σ . T 4

Substituindo os valores:

G t r = 0,283 . 0,4 . 0,4 . 5,67 . 10 - 8 . 1200 4

G t r = 5323,7   W

Resposta

τ = 0,283

G t r = 5 323,7   W

Exercício Resolvido #3

ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.

As variações da emissividade espectral de duas superfícies são indicadas na figura abaixo.

Determinar a emissividade média de cada superfície a T = 3000   K .

Além disso, determinar a absortividade e a refletividade média de cada superfície para a radiação proveniente de uma fonte a 3000   K .

Qual superfície é mais adequada para servir como um absorvedor solar?

Passo 1

Superfície (1):

A função de radiação do corpo negro será dada por:

λ 1 . T = 3 × 3000 = 9000   μ m . K → f λ 1 = 0,890029

Dessa forma, a sua emissividade média será:

ε = ε 1 . f λ 1 + ε 2 . 1 - f λ 1

ε = 0,2 × 0,890029 + 0,9 × 1 - 0,890029

ε = 0,28

Agora que encontramos a emissividade média, a absortividade média será:

α = ε

α = 0,28

Considerando as duas superfícies como opacas, τ = 0 , logo:

α + ρ = 1 → ρ = 1 - α = 1 - 0,28

ρ = 0,72

Passo 2

Superfície (2):

A função de radiação do corpo negro será dada por:

λ 1 . T = 3 × 3000 = 9000   μ m . K → f λ 1 = 0,890029

Dessa forma, a sua emissividade média será:

ε = ε 1 . f λ 1 + ε 2 . 1 - f λ 1

ε = 0 , 8 × 0,890029 + 0 , 1 × 1 - 0,890029

ε = 0 , 72

Agora que encontramos a emissividade média, a absortividade média será:

α = ε

α = 0 , 72

Considerando as duas superfícies como opacas, τ = 0 , logo:

α + ρ = 1 → ρ = 1 - α = 1 - 0 , 72

ρ = 0 , 28

Passo 3

Qual superfície é mais adequada para servir como um absorvedor solar?

A segunda superfície é mais adequada por apresentar uma maior absortividade média.

Resposta

Superfície (1):

ε = 0,28

α = 0,28

ρ = 0,72

Superfície (2):

ε = 0,72

α = 0,72

ρ = 0,28

A superfície (2) é mais adequada.

Exercício Resolvido #4

ÇENGEL, YUNUS A. Transferência de Calor de Massa, Uma Abordagem Prática. 3ed.

A variação da absortividade espectral de uma superfície é dada na figura abaixo.

Determinar a absortividade e a refletividade média da superfície para a radiação originária de uma fonte a T = 2500   K . Além disso, determinara a emissividade média desta superfície a 3000   K .

Passo 1

A absortividade média será dada por:

α = α 1 . f λ 1 + α 2 . 1 - f λ 1

Onde:

λ 1 . T = 2 × 25 00 = 5 000   μ m . K → f λ 1 = 0 , 633747

Logo:

α = 0,2 × 0 , 633747 + 0,7 × 1 - 0 , 633747

Considerando a superfície como opaca, τ = 0 , logo:

α + ρ = 1 → ρ = 1 - α = 1 - 0,38

Passo 2

A emissividade média será dada por:

ε = ε 1 . f λ 1 + ε 2 . 1 - f λ 1

Onde:

λ 1 . T = 2 × 30 00 = 6 000   μ m . K → f λ 1 = 0 , 737818

Logo:

ε = 0,2 × 0,737818 + 0,7 × 1 - 0,737818

Resposta

α = 0,38

ρ = 0,62

Para T = 3000   K , ε = 0,33 .

Exercício Resolvido #5

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

Um grande corpo de um gás não-luminoso a uma temperatura de 1200   K possui bandas de emissão entre 2,5 e 3,5   μ m e entre 5 e 8   μ m .

A emissividade na primeira banda é de 0,8 e na segunda banda é de 0,6 . Determine o poder emissivo desse gás.

Passo 1

O poder emissivo é dado por:

E g = ε . σ . T 4

No entanto, precisamos calcular a emissividade do gás. Como ele possui emissividade em duas bandas de frequência, podemos determinar a emissividade total do gás da seguinte forma:

ε = ε 1 . f 2,5 μ m → 3,5 μ m + ε 2 . f 5 μ m → 8 μ m

ε = ε 1 . f 3,5 μ m - f 2,5 μ m + ε 2 . f 8 μ m - f 5 μ m

Vamos determinar agora os valores das funções de radiação do corpo negro.

Passo 2

λ 1 . T = 2,5 × 1200 = 3000   μ m . K → f 2,5 μ m = 0,273

λ 2 . T = 3 , 5 × 1200 = 4200   μ m . K → f 3,5 μ m = 0,516

λ 3 . T = 5 × 1200 = 6000   μ m . K → f 5 μ m = 0,738

λ 4 . T = 8 × 1200 = 9600   μ m . K → f 8 μ m = 0,905

Assim, a emissividade será dada por:

ε = ε 1 . f 3,5 μ m - f 2,5 μ m + ε 2 . f 8 μ m - f 5 μ m

ε = 0,8 × 0,516 - 0,273 + 0,6 × 0,905 - 0,738

ε = 0,295

Passo 3

Finalmente, o poder emissivo será:

E g = ε . σ . T 4

E g = 0,295 × 5,67 × 10 - 8 × 1200 4

Resposta

E g = 34684   W / m 2

Exercício Resolvido #6

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

(Adaptado) A absortividade hemisférica espectral de uma superfície opaca tem o comportamento mostrado a seguir.

Qual é a absortividade solar, α s ?

Passo 1

A absortividade solar pode ser calculada utilizando as funções de radiação do corpo negro, da seguinte forma:

α s = α 1 . f 0 → λ 1 + α 2 . f λ 1 → λ 2 + α 3 . f λ 2 → ∞

α s = α 1 . f λ 1 - f 0 + α 2 . f λ 2 - f λ 1 + α 3 . f ∞ - f λ 2

Onde f 0 = 0 e f ∞ = 1 , logo:

α s = α 1 . f λ 1 - 0 + α 2 . f λ 2 - f λ 1 + α 3 . 1 - f λ 2

α s = α 1 . f λ 1 + α 2 . f λ 2 - f λ 1 + α 3 . 1 - f λ 2

Passo 2

Os valores da função de radiação do corpo negro são tabelados. Para determina-los, vamos precisar dos seguintes valores:

λ 1 = 0,3   μ m

λ 2 = 1,5   μ m

T = 5800   K

Dessa forma:

λ 1 . T = 0,3 × 5800 = 1740   μ m . K → f λ 1 = 0,0335

λ 2 . T = 1,5 × 5800 = 8700   μ m . K → f λ 2 = 0,8805

Passo 3

A absortividade solar será:

α s = α 1 . f λ 1 + α 2 . f λ 2 - f λ 1 + α 3 . 1 - f λ 2

Onde:

α 1 = 0

α 2 = 0,9

α 3 = 0,1

Logo, substituindo os valores:

α s = 0 × 0,0335 + 0,9 × 0,8805 - 0,0335 + 0,1 × 1 - 0,8805

Resposta

α s = 0,774

Exercício Resolvido #7

INCROPERA, F. P, DEWITT, D. P. Fundamentos de Transferência de Calor e Massa. 6ed.

A absortividade espectral α λ e a refletividade espectral ρ λ de um material difuso espectralmente seletivo são mostradas a seguir.

a Esboce a transmissividade espectral τ λ .

b Se a irradiação solar com G s = 750   W / m 2 e a distribuição espectral de um corpo negro a 5800   K incide sobre esse material, determine as frações da irradiação que é transmitida, que é refletida e que é absorvida pelo material.

c Se a temperatura desse material é de 350   K , determine a emissividade ε .

d Determine o fluxo térmico radiante líquido para o material.

Passo 1

a Esboce a transmissividade espectral τ λ .

A absortividade α λ , a refletividade ρ λ e a transmissividade τ λ apresentam a seguinte relação:

α λ + ρ λ + τ λ = 1

τ λ = 1 - α λ - ρ λ

Para 0 ≤ λ ≤ 1,38   μ m :

α λ = 0,2

ρ λ = 0,1

τ λ = 1 - 0,2 - 0,1 → τ λ = 0,7

Para λ ≥ 1,38   μ m :

α λ = 1

ρ λ = 0

τ λ = 1 - 1 - 0 → τ λ = 0

Assim, graficamente, a transmissividade será dada por:

Passo 2

b Se a irradiação solar com G s = 750   W / m 2 e a distribuição espectral de um corpo negro a 5800   K incide sobre esse material, determine as frações da irradiação que é transmitida, que é refletida e que é absorvida pelo material.

A transmissividade da superfície pode ser calculada através das funções de radiação do corpo negro, onde:

τ s = τ 1 . f 0 → λ 1 + τ 2 . f λ 1 → ∞

τ s = τ 1 . f λ 1 - f 0 + τ 2 . f ∞ - f λ 1

Onde f 0 = 0 e f ∞ = 1 , logo:

τ s = τ 1 . f λ 1 - 0 + τ 2 . 1 - f λ 1

τ s = τ 1 . f λ 1 + τ 2 . 1 - f λ 1

Onde:

λ 1 . T = 1,38 × 5800 = 8000   μ m . K

f λ 1 = 0,856

Substituindo os valores:

τ s = 0,7 × 0,856 + 0 × 1 - 0,856

Passo 3

Para a refletividade, vamos fazer a mesma coisa que acabamos de fazer:

ρ s = ρ 1 . f λ 1 + ρ 2 . 1 - f λ 1

ρ s = 0 , 1 × 0,856 + 0 × 1 - 0,856

Passo 4

Para a absortividade, basta utilizar a seguinte relação:

α s + ρ s + τ s = 1

α s = 1 - ρ s - τ s

Substituindo os valores:

α s = 1 - 0,0856 - 0,599

Passo 5

c Se a temperatura desse material é de 350   K , determine a emissividade ε .

Nesse caso, precisamos definir novamente a função de radiação do corpo negro. Considerando que ε λ = α λ , teremos:

ε = α 1 . f λ 1 + α 2 . 1 - f λ 1

A função de radiação será dada por:

λ 1 . T = 1,38 × 350 = 483   μ m . K

Para esse valor, f λ 1 = 0 , logo:

ε = α 2

Passo 6

d Determine o fluxo térmico radiante líquido para o material.

O fluxo radiante será dado por:

q r a d ' ' = G s - ρ s . G s - τ s . G s - E

q r a d ' ' = α s . G s - E = α s . G s - σ . T 4

Substituindo os valores:

q r a d ' ' = 0,315 × 750 - 5,67 × 10 - 8 × 350 4

Resposta

a

b τ s = 0,599 , ρ s = 0,0856 , α s = 0,3154

c ε = 1

d q r a d ' ' = - 615   W / m 2

Exercício Resolvido #8

Questão 1, UFRJ, P1-2004.2

A superfície de uma nave espacial é composta de uma placa metálica bem fina, internamente isolada à transferência de calor. A face externa da placa tem absortividade de 0,3 para a radiação solar incidente, que é de 1000   W / m 2 .

A emissividade da superfície externa da placa é 0,8 e a temperatura do envoltório para a troca de calor por radiação é 0   K . No regime permanente, calcule a temperatura da placa, a qual é suposta uniforme.

Passo 1

Sobre a superfície da nave, incide uma radiação solar de intensidade 1000   W / m 2 . Como a absortividade é igual a 0,3, a quantidade de calor absorvida pela placa será:

q = 0,3 × 1000 = 300   W / m 2

Passo 2

Como a temperatura do envoltório é de 0   K . A taxa de transferência de calor será dada por:

q = ε . σ . T 4

300 = 0,8 × 5,67 × 10 - 8 × T s 4

Resposta

T s = 285,2   K

Exercícios de Livros Relacionados

A radiação solar incide sobre a superfície frontal de uma placa fina com componentes direto e difuso de 300 e 250 W/m², respectivamente. A radiação direta faz um ângulo de 30° com a normal da superfíc
A emissividade direcional espectral de um material difuso a 2 5 00K apresenta a seguinte distribuição:Determine a emissividade hemisférica total a 2 5 00K . Determine o poder emissivo na faixa espectr
29 – Considere a superfície difusiva do Problema 12.28. Determine a emissividade da superfície hemisférica e a potência emitida em T = 300, 500, e 700 K. Em qual comprimento de onda o pico espectral d
Uma pequena superfície de área A 1 = 5 cm2 emite radiação como um corpo negro a T 1 = 1000 K. Um sensor de radiação de área A 2 = 3 cm2 é colocado na direção normal da visualização da superfície A 1 n
A variação da transmissividade espectral de uma janela de vidro de 0,6 cm de espessura é indicada na figura a seguir. Determine a transmissividade média dessa janela para a radiação solar ( T ≈ 5.800