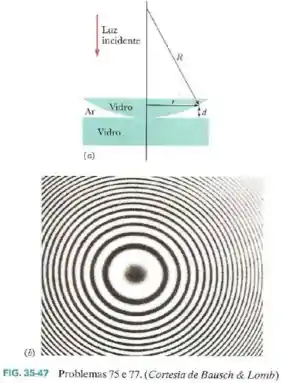
A Fig.35-47a mostra uma lente com raio de curvatura pousada em uma placa de vidro e iluminada de cima por uma luz de comprimento de onda .
A Fig.35-47b (uma fotografia tirada de um ponto acima da lente) revela a existência de franjas de interferência circulares (os chamados anéis de Newton) associadas à espessura variável do filme de ar que existe entre a lente e a placa.
Determine os raios dos anéis que correspondem aos máximos de interferência, supondo que .
Passo 1
O raio do anel é dado por . Pela figura, vemos que para um ponto do filme fino de espessura , forma-se um triângulo retângulo de lados , e .
Este último é porque a lente é esférica: a distância do centro de curvatura até o centro da lente será .
Como é um triângulo retângulo, podemos usar a equação de Pitágoras:
O problema nos diz que a espessura do filme fino é muito menor do que o raio de curvatura, ou seja:
Se dividirmos nossa equação por :
Como , nós podemos desprezar o segundo termo da equação, e obter:
Passo 2
Sendo a espessura do filme de ar (e, sendo um filme de ar, consideramos que que é menor que o da placa e o da lente), a condição para os máximos de interferência será:
O que nos permite encontrar a espessura com base na ordem do máximo.
Se substituirmos esse valor na equação anterior: