Equações do Movimento em Notação Vetorial
Produzido por Ludovic BeghinTeoria
Equações do Movimento em Notação Vetorial
Vamos ver como aplicar as equações do movimento uniforme e do movimento uniformemente variado em um movimento bidimensional ou tridimensional.
A primeira ideia que temos que construir para entender tudo desse assunto é que o movimento de um objeto em um eixo é completamente independente do movimento do mesmo objeto em outro eixo.
Isso que acabei de lhe dizer significa que um objeto pode mover-se no eixo em um movimento acelerado, no eixo ele pode estar parado e no eixo estar executando um movimento uniforme.
Então não se assuste se ver que o movimento em um eixo é diferente do movimento em outro eixo.
Mas, vamos as fórmulas né! Bem, as equações vão continuar as mesmas pois o tempo é um escalar.
Equação da posição
Equação da velocidade
Vamos ver um exemplo!
Uma bola passa na origem com aceleração e velocidade . Qual é a posição e a velocidade dessa bola depois de passar na origem.
Vamos calcular a posição da bola usando a equação da posição
Como no inicio ele estava na origem, temos que , e vamos substituir nossos vetores na equação
Vamos agora juntar tudo que for de um eixo
Observe que no eixo temos um movimento acelerado, no eixo a bola ta parada e no eixo a bola executa um movimento uniforme.
Vamos calcular
Agora, para calcular vamos usar a equação da velocidade
Reescrevendo a equação juntando as informações de cada eixo
Bom já resolvemos o problema, mas poderíamos ter resolvido o problema analisando o movimento em cada eixo separadamente e assim trabalhando como se o movimento fosse unidimensionalmente pois os movimentos são independentes entre os eixos.
Vamos aos exercícios fixar tudo que aprendemos!
Exercícios Resolvidos
Exercício Resolvido #1
DEF.FE
Um corpo encontra-se inicialmente (em unidades do SI) com velocidade . Em qualquer instante, a aceleração é dada pela expressão . Encontre a expressão para a velocidade em função do tempo.
Passo 1
Para a velocidade, podemos usar a formulinha da velocidade!
Essa aqui ó:
Show! Temos a velocidade inicial e a aceleração, então:
Agora somando as componentes no mesmo eixo coordenado, temos:
Prontinho!
Resposta
Exercício Resolvido #2
UNIVAP
Uma partícula, cuja velocidadeem t=0, sofre uma aceleração constante de módulo , que faz um ângulo com o eixo-x positivo. Qual é, aproximadamente, a velocidade em ?
Obs: Pega a calculadora que vai te ajudar :D
Passo 1
Como temos uma aceleração constante, podemos usar essa formulinha aqui ó:
Né não? Mas pra descobrirmos o vetor velocidade, como temos componentes no eixo x e no eixo y, podemos dividir essa equação pra cada eixo, né? Ou seja:
Então vamo lá! Primeiro passo é encontrar nossa aceleração nos dois eixos coordenados x e y. Como essa aceleração faz um ângulo de com o eixo x, temos que:
Show! Primeira parte já foi.
Passo 2
Agora que temos nossas acelerações em cada um dos eixos coordenados, quando jogamos seus valores nas equações com , temos:
Aproximando as valores como a questão nos pede, temos:
Conseguimos! Acabamos! :D
Resposta
Exercício Resolvido #3
Paul A. Tripler e Gene Mosca, Física Para Cientistas e Engenheiros, Volume 1, 6ª edição, Cap 3, pp 86 xx 50
No tempo zero, uma partícula está em e e tem a velocidade . A aceleração da partícula é constante e dada por . Encontre a velocidade em Expresse o vetor posição em em termos de e . Além disso, dê a magnitude e a orientação do vetor posição neste tempo.
Passo 1
O problema quer a velocidade e a posição da partícula em um determinado tempo. Para isso vamos usar as equações do movimento.
Passo 2
Vamos encontrar a velocidade em , para isso vamos usar a fórmula da velocidade
Passo 3
Agora vamos encontrar a posição da partícula no momento , faremos isso utilizando da equação da posição.
Passo 4
Quando escrevemos algo em notação vetorial a orientação já está clara no vetor, então nos resta encontrar a magnitude desse vetor. Bom, isso é o mesmo que achar o tamanho do vetor, ou seja, o problema quer o módulo, então faremos isso.
Resposta
Exercício Resolvido #4
DEF.FE
Um canhão dispara uma bala, desde o terraço de um edifício, na posição (unidades SI):
com velocidade inicial (unidades SI):
em que o eixo dos z aponta na direção vertical, para cima, e com origem no chão. Admitindo que a resistência do ar pode ser desprezada, calcule a altura máxima atingida pela bala e a posição em que a bala bate no chão.
Obs: Pega a calculadora que cê pode precisar ;)
Passo 1
Usando o sistema de eixos definido no enunciado do problema como z na vertical, o vetor aceleração é , sendo a gravidade. A expressão do vetor velocidade em função de um instante t qualquer obtém-se a partir da equação das velocidades, né? Aquela lá:
Então vamo lá! Substituindo nossos dados, temos:
Juntando cada coordenada, temos:
A altura máxima será atingida no instante em que a velocidade seja nula na vertical, ou seja, no nosso caso, quando a componente da velocidade for nula. Show, né? Então devemos igualar a componente em z a 0.
Como queremos a altura máxima, temos que substiruir esse tempo na equação da posição na direção z:
Substituindo os dados:
Passo 2
Agora pra gente encontrar a posição onde a bala bate no chão, sabemos que a equação do espaço é dada por:
Para calcular o instante em que a bala bate no chão, ou seja, o instante onde a altura Z é igual a 0, calcula-se o tempo t em que a componente z da posição é igual a zero, né? :p Então vamo lá:
Usando Bháskara nessa equaçãozinha do segundo grau, temos que:
E pra gente descobrir a posição da bala nesse instante é só substituirmos esse valor de t na equação do espaço! Vamo nessa:
Resposta
e
Exercício Resolvido #5
David Halliday, Robert Resnick, Jearl Walker, Fundamentos de Física, volume 1 , 8º ed. Rio de Janeiro: LTC , 2008, pp 85-17
Uma partícula deixa a origem com uma velocidade inicial e uma aceleração constante . Quando ela atinge o máximo valor de sua coordenada , quais são a sua velocidade e o seu vetor posição?
Passo 1
O problema quer a velocidade e posição da partícula quando ela atinge o máximo valor de sua coordenada . Bom, aqui entra uma parte teórica importante, vamos observar os dados que temos sobre o movimento no eixo
A partícula só se moverá para frente (sentido positivo do eixo ) se a velocidade for positiva. No momento que a velocidade for negativa a partícula começará a voltar no eixo movendo-se para trás. Como a aceleração é negativa sabemos que ela irá diminuir o valor da velocidade.
Passo 2
Assim, teremos o máximo valor na coordenada quando a velocidade for zero,. Vamos calcular isso então, analisando apenas o eixo .
Como estamos estudando apenas o movimento no eixo podemos trabalhar como se fosse um movimento unidimensional e por isso
Onde a velocidade final é zero , a velocidade inicial é e a aceleração é .
Agora vamos analisar o movimento no eixo , pois já sabemos o instante em que a partícula atinge o máximo valor da coordenada , como queremos saber a velocidade em neste instante, basta sunstituir na equação da velocidade.
Onde e aceleração é
Agora que já descobrimos a velocidade em cada eixo, vamos escrever o vetor velocidade
Passo 3
Como já descobrimos o instante de tempo em que a partícula atinge o máximo valor da coordenada do eixo . Basta substituirmos esse na equação da posição que acharemos o vetor posição.
Resposta
Exercício Resolvido #6
UNICAMP-1ªProva-2013.2
Na figura abaixo, a partícula se move ao longo da reta com uma velocidade constante paralela ao eixo . No instante de tempo em que a partícula passa pelo eixo , a partícula deixa a origem com velocidade inicial zero e aceleração constante de módulo , o ângulo entre e o semi-eixo positivo é .
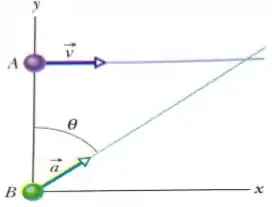
Escreva uma expressão para a velocidade da partícula .
Escreva uma expressão para a posição da partícula em função do tempo.
Escreva uma expressão para a posição da partícula em função do tempo.
Que valor de velocidade deve ter a particula para que aconteça a colisão?
Passo 1
Basta lembrar da fórmula que diz que . Mas como a velocidade inicial da partícula é nula e ela está inclinada aos eixos e , teremos que decompor ela assim:
Passo 2
Nessa teremos que lembrar da fórmula , a partícula não tem aceleração. Então vamos decompor nos eixos e assim:
Passo 3
Novamente vamos utilizar a fórmula , só que na partícula não tem velocidade inicial e a posição inicial é zero. Então vamos decompor assim:
Passo 4
Para que aconteça a colisão para o mesmo instante de tempo, assim obtemos:
Igualando em :
Igualando em :
E, portanto:
Resposta
Exercício Resolvido #7
UNICAMP-1ª Prova-2010
As “lentes” de um microscópio eletrônico consistem em campos elétricos e magnéticos que controlam um feixe de elétrons. Como um exemplo da manipulação do feixe de elétrons, considere um elétron afastando-se da origem ao longo do eixo no plano com velocidade inicial . Sua aceleração pode ser decomposta em uma componente na mesma direção que a velocidade inicial, de módulo e outra no sentido perpendicular, com módulo .
Determine:
A expressão para a posição do elétron em função do tempo e a posição deste quando .
A expressão para a velocidade do elétron em função do tempo e a velocidade quando .
A velocidade escalar do elétron quando .
(d) A direção da trajetória do elétron.
Passo 1
Vamos utilizar nossa já conhecida fórmula:
Para o eixo :
Para o eixo :
Logo temos que:
Quando :
Por bhaskara encontramos o valor de :
Como o tempo não pode ser negativo, vamos ignorar o resultado negativo e considerar só o positivo:
Agora é só substituir esse instante de tempo na equação da posição.
Passo 2
Precisamos utilizar a fórmula da velocidade:
Em descobrimos no item anterior que , então:
Passo 3
Já temos a velocidade vetorial, para achar a escalar é só tirar o módulo. Lembra da fórmula do módulo de um vetor?
Passo 4
Basta encontramos o ângulo que o vetor velocidade faz com o eixo . Para isso é só imaginar um triângulo retângulo em que o cateto oposto é a componente e o cateto adjacente é a componente .
Resposta
;
Exercício Resolvido #8
USP-1ªProva-2013-Modificado
Um elétron de massa e velocidade horizontal incide em uma região entre duas placas paralelas eletricamente carregadas, conforme mostra a figura abaixo. Ao percorrer essa região o elétron é submetido a uma forca vertical , constante, para cima (sabe-se que ). Sabendo-se que o comprimento das placas é igual a e desprezando o efeito da aceleração da gravidade, determine:
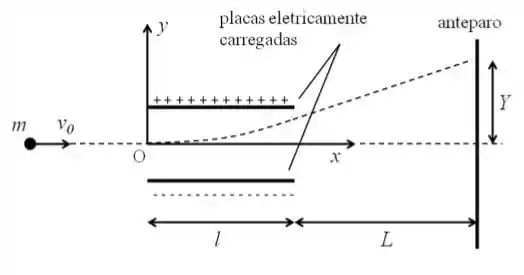
O vetor posição do elétron em função do tempo, quando este se encontra entre as placas paralelas eletricamente carregadas. Considere que a origem do sistema de coordenadas é do lado esquerdo das placas e que o elétron passa pela origem do sistema de coordenadas no instante , conforme mostra a figura. Expresse o resultado em termos de , , , e .
O valor de , quando o elétron atinge um anteparo situado a uma distancia das placas paralelas. Expresse o resultado em termos de , , , , .
Passo 1
Vamos calcular sua equação para o eixo primeiramente:
Não temos nenhuma força atuando no eixo , logo a aceleração e nula. Dai tiramos que o movimento no eixo corresponde a um MRU que obedece a fórmula:
Temos também que o movimento se inicia na origem das placas, logo .
Vamos agora calcular a equação para o eixo :
Para o eixo , temos uma força constante, logo a aceleração também é constante. Dai tiramos que o movimento no eixo corresponde a um MUV que obedece a fórmula:
Entretanto, temos que e que , ficando apenas com:
Utilizando o dado do enunciado que :
Substituindo:
Logo, teremos para o vetor posição:
Passo 2
Primeiramente precisamos saber quando que a força vai parar de atuar, que é no final da distância das placas que pode ser calculada com a expressão do item anterior.
Logo, neste instante a equação da posição muda, por que agora o eixo não terá mais a força atuando e portanto também não terá mais aceleração, passando a ser um movimento MRU dado por:
Onde é a posição quando e é a componente da velocidade neste mesmo instante . Vamos calcular isso.
O vetor velocidade pode ser calculado por:
Logo:
Logo:
Muito bem, agora para achar :
Temos então que:
Substituindo o valor de :
Portanto nosso novo é:
O projétil irá atingir o anteparo no instante:
Portanto: