Força eletromotriz
Produzido por Bruno SoaresTeoria
A força eletromotriz (fem) representa o trabalho realizado pelo movimento de cada carga em um circuito.
O que é Força Eletromotriz?
Apesar do nome, a Força Eletromotriz NÃO é uma força. Na verdade, a fem é uma diferença de potencial (uma ”voltagem”).
A força eletromotriz pode ser compreendida como a quantidade de trabalho
A fem pode ser calculada pela seguinte fórmula:
Onde:
é a força eletromotriz, em volts ; é o trabalho realizado pela fonte, em Joule ; é carga que percorre o circuito em coulomb .
Podemos escrever a fórmula da força eletromotriz na sua forma diferencial:
Onde
Entendendo a Força Eletromotriz na Prática
Pra ficar claro o que é a força eletromotriz na prática, vamos dar uma olhada no circuito simples abaixo:
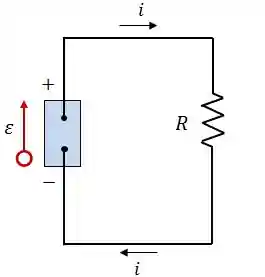
Nesse circuito nós temos uma fonte de energia (bateria, pilha, etc…), e a função dela é manter uma diferença de potencial entre o lado positivo e o lado negativo.
Então imagine comigo! Uma carga positiva sai do terminal positivo da fonte de fem para percorrer o circuito, quando a carga passa por um resistor ela “gasta” o potencial que ela tinha, dá a volta e chega no terminal negativo da fonte de fem.
É aí que está a mágica da fonte... ela realiza um trabalho sobre essa carga positiva para que ela passe do terminal negativo para o terminal positivo da fonte e recomece o ciclo.
Fonte Ideal
Uma fonte ideal não possui nenhuma resistência no seu interior. Assim, a diferença de potencial entre os seus terminais é igual à força eletromotriz.
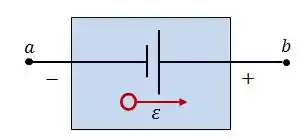
Fonte Real
Uma fonte real possui uma resistência interna que, mesmo sendo geralmente pequena, atrapalha o movimento das cargas. Assim, a diferença de potencial entre os terminais da fonte será menor que a força eletromotriz.
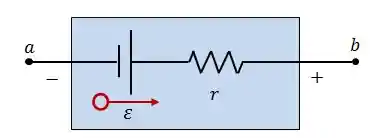
Então podemos dizer que:
Vídeo aula- Força Eletromotriz
Ficou com alguma dúvida sobre Força Eletromotriz? Confere então essa vídeo aula super completa que o Responde Aí preparou pra você!
Agora, confere aqui em baixo que temos um monte de exercícios pra você praticar 👇