Teoria
Fala ai e bem vindo ao RespondeAi! Vamos falar um pouco sobre física? Mais especialmente sobre como podemos aplicar forças em objetos que são capazes de girar em volta de um eixo de rotação. Como sempre vamos começar pensando em um exemplo.
O melhor exemplo para falarmos sobre Torque é o exemplo da porta e da maçaneta. Você já reparou que a maçaneta da porta sempre fica no lado oposto ao ponto de fixação da porta na parede? Porque isso acontece? Vamos tentar entender isso com calma?
Confere esse desenho, de uma porta vista de cima:
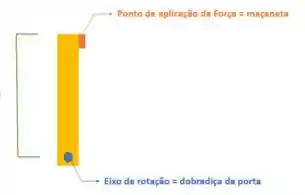
Imagina essas duas situações:
- a primeira vamos aplicar uma força perpendicular a porta:
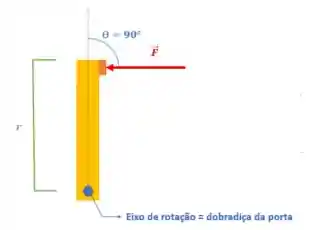
- na segunda vamos aplicar uma força na direção da reta que liga a dobradiça e a maçaneta:
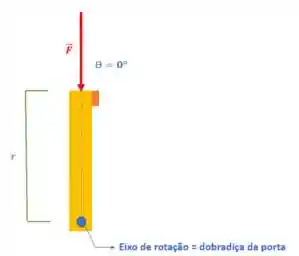
Você pode até fazer esse teste ai na sua própria casa, e verificar, que aplicando a força da primeira forma, faz a porta girar, enquanto aplicar a força da segunda forma não funciona.
Isso acontece exatamente por causa do conceito de torque.
Torque
O Torque é um vetor que representa a tendência que uma força tem para rotacionar um corpo ao redor de um eixo de rotação, quando a força empurra a porta com uma orientação de
Podemos calcular o torque com a fórmula:
Então o torque é o produto vetorial entre o vetor
Dessa fórmula podemos entender porque faz sentido a maçaneta ficar sempre do lado oposto ao ponto de rotação da porta, quando colocamos a maçaneta mais longe, aumentamos o braço de alavanca, e por isso precisamos fazer menos esforço para gerar torque e abrir/fechar a porta.
Módulo do Torque
Nem sempre estamos trabalhando com vetores, então podemos simplificar esse produto vetorial e calcular o módulo do torque com a fórmula:
Ou seja, o torque vai variar de acordo com o módulo do vetor braço, o módulo do vetor foça e o seno do ângulo que existe entre esses dois vetores..
Vamos fazer um exemplo:
Se aplicarmos uma força com módulo igual a
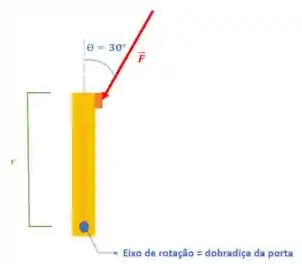
Qual será o módulo do Torque exercido por essa força?
Usando a fórmula do Torque, podemos escrever:
Regra da Mão Direita
Já ouviram falar da regra da mão direita né? Ela sempre vai aparecer quando tiver fazendo um produto vetorial, a gente vê isso em álgebra linear, vou relembrar para vocês. Nós sabemos que dois vetores formam um plano, em alguma aulinha o professor de vocês deve ter falado que quando a gente faz o produto vetorial entre esses dois vetores, o vetor resultante surge perpendicular ao plano formado por esses dois vetores.
E é exatamente isso que acontece no caso do produto vetorial entre braço e força que gera o torque. Ou seja, o torque vai ser um vetor perpendicular ao plano formado pelos vetores
Shoow, mas e regra da mão direita? A regra da mão direita é um macete que permite a gente descobrir de maneira simples qual a direção em que o vetor Torque aponta, porque ele pode apontar tanto na direção positiva do eixo a que ele pertence, quanto na direção negativa do eixo a que ele pertence e é a regra da mão direita que vai definir isso para gente.
Nós temos uma página de conceito escrita pelos nosso Experts, que explica para você como funciona a Regra da Mão Direita. Ou você pode assistir ao vídeo do exercício aqui em baixo para se lembrar como fazemos ela.
Exercícios
Vou deixar vocês agora com uma resolução Passo a Passo de um exercício de Torque. Aproveita e começa a fazer exercícios para entender direitinho como funciona a Regra da Mão Direita e não errar na hora da prova! Bons estudos!