Torque em Polias Não-Ideais
Produzido por Ludovic BeghinTeoria
Se liga, sempre que você começa a ver em física algo do tipo “não ideal” é sinal que você tá evoluindo no estudo.
Mas e ae o que você acha que vai influenciar a polia não ser ideal?
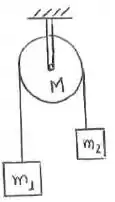
Agora a polia possui massa, sendo assim, ela vai passar a ser um corpo do nosso sistema e vamos precisar considera-la no diagrama do corpo livre.
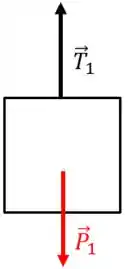
Vamos olhar pra imagem.
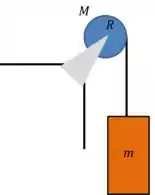
Show, já vimos algo muito parecido com isso antes quando trabalhamos com uma polia ideal. Mas, e se eu pedir a você a aceleração angular da polia? Complica um pouco?
Então vamos descomplicar isso aí juntos! Vamos passo-a-passo.
Dados : ;; .
Passo 1
Primeiro passo é o mesmo de sempre! Vamos desenhar o diagrama de corpo livre de cada um dos corpos e analisar quais forças atuam sobre eles.
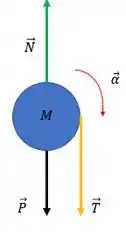
Polia:
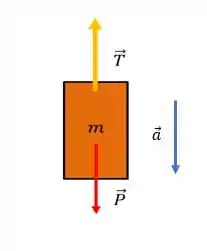
Bloco:
A relação da aceleração angular pode ser tirada através da segunda lei de newton para rotaç��o:
Onde é o torque que precisamos encontrar e é o momento de inércia da polia que é constante.
Já a aceleração do bloco a gente tira pela segunda lei de newton, ou seja:
Passo 2
Vamos começar pelo mais simples, analisando o bloco para encontrar uma expressão para a tração, a qual relacionaremos com a polia depois. Pra isso vamos dar uma olhada no DCL do bloco de novo.
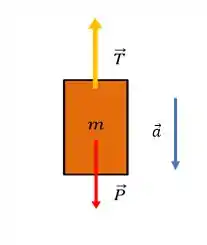
Usando a Segunda Lei de Newton com o referencial positivo para baixo, pois a aceleração do bloco aponta para baixo, assim temos:
Substituindo os valores temos:
Passo 3
Precisamos analisar as forças que agem na polia, para aí sim termos o valor de e relacionar também com a tração.
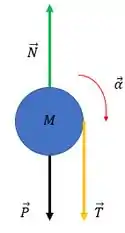
Nosso eixo de rotação passa pelo centro da polia, que bom pra nós! Com isso, podemos ignorar tanto a força peso quanto a força normal, sendo assim o torque na polia vai ser dado por:
Considerando o sentido horário como positivo já que vai no sentido da aceleração angular. Já encontramos uma relação de com a tração mas dá pra melhorar isso certo? Vamos usar a segunda lei de newton da rotação:
E como a polia é um disco que rotacional ao redor do centro de massa:
E igualando a relação da tração temos:
Mas beleza, chegamos numa equação para a tração com relação a aceleração angular da polia. Enquanto para o bloco, tínhamos uma equação para a tração com relação a aceleração do bloco, será que podemos relacionar as duas coisas?
Passo 4
Se liga nesse pulo do gato!

Como a corda não desliza sobre a polia, a aceleração com que o bloco cai é a mesma aceleração linear de qualquer ponto por onde a corda passa
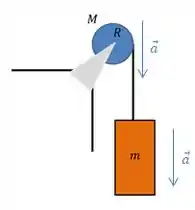
E a corda passa ao redor da polia, com isso, podemos relacionar a aceleração do bloco com a aceleração angular da polia:
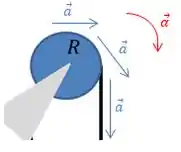
Portanto, em polias não ideias podemos usar a relação:
Ou então:
E substituindo na lei de newton da polia:
Agora sim, substituindo os valores:
Passo 5
Agora é só montar o sistema e partir pro abraço:
Resolvendo esse sisteminha, igualando as trações, você encontra que:
Que é a aceleração do bloco!
Para encontrar a tração na corda, a gente pode fazer:
E pra fechar, como a gente queria encontrar a aceleração angular da polia, a gente pode usar a relação:
Conclusão
A polia não ideal deve ser sempre considerada como um corpo que faz parte do sistema. Usaremos para ela sempre a segunda lei de newton da rotação:
E para relacionar a aceleração da polia e do bloco a gente fz:
E tome sempre cuidado com os sinais! Considere a direção da aceleração e da aceleração angular como o positivo, que dá tudo certo!
Passo 2
Passo 3
Passo 4
Passo 5
Conclusão
Exercícios Resolvidos
Exercício Resolvido #1
USP-P3-2015-7.
Uma máquina de Atwood possui massas , e uma polia maciça uniforme de massa M =2,0kg. O módulo da aceleração linear da massa vale:
a)
b)
c)
d)
e)
Passo 1
Isolando as forças, teremos:
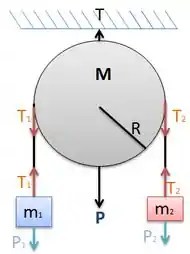
Duas forças em : e
Duas forças em : e
E quatro forças na Polia: (peso da polia), (reação pela polia estar presa ao teto), () e ( )
Passo 2
Vamos assumir que o bloco de massa está descendo e portanto se movimentando contra a orientação do nosso eixo vertical, então utilizando a segunda Lei de Newton para escrever as equações do movimento desse bloco, teremos:
Se o bloco desce, então o bloco sobe, teremos:
E não podemos esquecer de analisar o movimento de rotação da polia, já que a polia que faz parte do problema não é ideal. A polia não translada, mas pela Segunda Lei de Newton para rotação sabemos que e geram torque. Considerando a aceleração angular sendo positiva no sentido anti-horário, podemos escrever:
Passo 3
O da polia é dado por . Além disso, temos a relação .
Assim:
Passo 4
Agora montando um sistema com a equação do bloco de massa e do bloco , subtraindo a primeira da segunda, teremos:
Mas do Passo 3, pela equação do movimento de rotação da polia, sabemos que .
Substituindo na útima equação, teremos:
Passando para o outro lado, colocando em evidência, e substituindo os pesos por suas fórmulas correspondentes:
Isolando o :
Passo 5
Substituindo de vez agora os valores, teremos:
Como a aceleração do bloco é igual a , teremos:
Resposta
Letra D
Exercício Resolvido #2
PUCRIO-P3-2013.2-1
Um cabo ideal está enrolado em volta de uma polia de raio e massa e tem sua outra extremidade ligada a um bloco de . O bloco se encontra apoiado sobre um plano inclinado de em relação a horizontal. O sistema é solto a partir do repouso. Não existe atrito entre o plano e o bloco. Considerando o momento de inércia da polia , calcule:
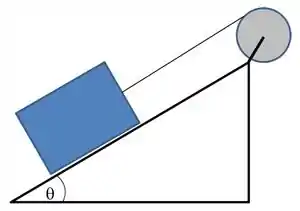
A aceleração angular da polia.
a tração no cabo e o torque na polia.
O módulo da aceleração linear de um ponto na borda na polia após de iniciado o movimento.
Passo 1
Para descobrir a aceleração angular da polia, devemos utilizar a fórmula do torque, onde .
No entanto, precisaremos de mais uma equação. Como existe um vínculo entre os dois corpos, podemos também usar , pois sabemos que .
Se liga nas equações:
Passo 2
Agora que já temos em função de , vamos à equação para o bloco:
Substituindo na equação, temos:
A aceleração angular fica:
Passo 3
Ahh...fazer esse item ficou fácil depois de ter feito o anterior! Queremos saber a tração , que a gente ja deixou em função de e de , lembra?!
Agora que a gente já tem o valor de , ficou fácil!
Já o torque da polia é dado por:
Passo 4
Para achar a aceleração linear, temos que achar a aceleração tangencial e a aceleração centrípeta, que são as componentes da aceleração linear. Lembra?! Vamos começar pela tangencial, a gente já calculou no item , mas vamos lá!
Agora vamos achar a centrípeta.
Sabemos que depois de , temos:
Então a aceleração centrípeta fica:
Passo 5
Agora que temos a aceleração tangencial e a aceleração centrípeta, basta fazer aquele Pitágoras básico para achar a aceleração linear! Olha só!
Resposta
;
Exercício Resolvido #3
UFRJ-p2-2012.1-M01
Dois discos de mesmo raio e de massa diferentes, onde , estão presos ao teto por fios ideais e enrolados em suas bordas. Liberados a partir do repouso eles caem verticalmente onde é o módulo da aceleração local da gravidade; o momento de inércia de um disco em torno do seu eixo de rotação que passa pelo seu centro é igual . Os módulos das trações nos fios em cada disco são e e as acelerações dos seus centros de massa são e , respectivamente, a opção correta abaixo é:
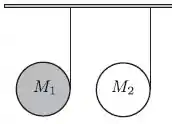
- ;
- e
Passo 1
Quando os discos caem eles descem verticalmente, isso quer dizer que eles rodam em torno do seu centro.
A única força que atua no disco fazendo torque é a tração, fazendo ele girar no sentido anti-horário
O enunciado disse o momento de inércia do disco, então
Lembrando que, nesse caso
Resultando em
Passo 2
Além disso as forças que atuam no disco, que são o peso e a tração vão ter a seguinte equação
O sinal da aceleração é importante para termos compatibilidade de movimentos, já que o disco roda no sentido anti-horário a aceleração é para baixo.
Substituindo o que achamos no passo 1
Então
Repara que eu fiz essa conta toda para um disco qualquer, por isso não disse se era ou . A aceleração não depende da massa, então elas são iguais
Resposta
Letra C
Exercício Resolvido #4
UFRJ-P2-2012.1-Q1.
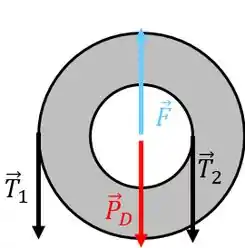
Considere dois discos um de raio e de massa e outro de raio e de massa unidos concentricamente formando um sistema (disco composto) rígido, cujo momento de inércia vale quando gira livremente em torno do eixo fixo e perpendicular ao plano dos discos passando pelo centro. Duas massas, e , presas a cordas finas e inextensíveis enroladas na periferia dos discos de raios e respectivamente, fazem girar o disco composto quando soltas; considere que é o módulo da aceleração local da gravidade.
- Isole os blocos e o disco composto e represente em um diagrama de corpo livre todas as forças, identificando-as, que atuam em cada um deles; use como referência a vista lateral do sistema.
- Escreva as equações do movimento de rotação do disco composto e de translação dos blocos.
- Determine a aceleração angular, , do disco composto.
- Determine matematicamente a condição para que o sistema esteja em equilíbrio
Passo 1
a)
Vamos começar fazendo o DCL do bloco .
Nesse caso, só vamos ter a tração e a força peso atuando.
Passo 2
Agora no bloco será a mesma coisa que no bloco , só os pesos e as trações que são diferentes:
Passo 3
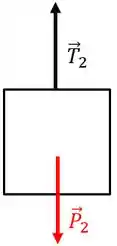
No disco, o DCL é o seguinte:
Nesse caso, temos as duas forças de tração, o peso do disco e a força de reação do pino que chamei de .
Passo 4
b)
Vamos considerar que o disco rola com aceleração angular no sentido anti-horário. É importante, em questões mais complexas como essa, olharmos a rotação do disco direito e com calma.
Vamos ter:
Então:
Passo 5
Se o disco está rolando no sentido anti-horário, o bloco está subindo e o bloco está descendo. Chamando cada módulo da aceleração de e , as equações do movimento serão as seguintes.
Para o bloco :
Lembrando que:
Resultando em:
Passo 6
Agora para o bloco :
Lembrando que:
Resultando em:
Passo 7
c)
Temos as seguintes equações:
Multiplicando a segunda equação por e a terceira equação por :
Agora somando todas as equações vamos ter:
Passo 8
Para que o sistema esteja em equilíbrio, devemos ter:
Então: