Energia Cinética de Rotação
Teoria
Rotação pura
Vamos pensar em uma situação intrigante. Suponha que você esteja rodando uma manivela que movimenta uma grande roda, como na imagem abaixo:
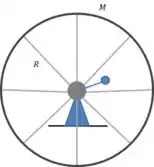
A roda possui massa e raio . Você então aplica força na extremidade da manivela, fazendo o disco começar um movimento de rotação. Qual a energia cinética gasta nesse movimento? Se a velocidade angular é .
Ah, moleza a energia cinética é dada por:
Mas pera aí, essa roda tá fixa ou seja o centro de massa dela tem velocidade zero. Então:
Se disséssemos que a energia gasta pra colocar a roda em movimento é nula, você acreditaria? Acho que não, né?
A sua intuição não te enganou! Vamos aprender aqui sobre a energia cinética de rotação, que é usada quando objetos giram e ganham energia. No nosso caso o eixo de rotação está parado, não há movimento de translação, isso é a rotação pura!
Mas o que é o eixo de rotação?
Nada mais é do que o eixo onde o objeto gira em torno, vamos desenhar o objeto em 3 dimensões e definir os eixos pra ver qual é o eixo de rotação.
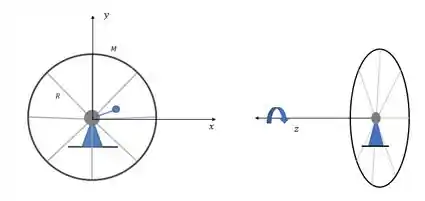
Na nossa figura o eixo de rotação é o eixo pois a roda gira em torno dele, e repare que esse eixo não se movimenta, é travado pelo apoio.
Tá, beleza... Mas, como eu calculo essa energia de rotação?
Simples! Só usar a fórmula:
Onde:
- é a energia cinética de rotação;
- é o momento de inércia do corpo e nesse caso é dado por:
- e é a velocidade angular do corpo no instante desejado dado.
E substituindo os valores do nosso exemplo temos:
Substituindo tudo na nossa fórmulinha, temos:
Com isso podemos dizer que a energia cinética da nossa roda vai ser de!
E se liga para a roda do nosso problema o eixo de rotação está parado e portanto não possui energia de translação, mas em outros corpos como planetas essa energia existe e é calculada como a energia cinética comum:
Isso porquê o eixo de rotação de objetos como planetas se movimenta com o passar do tempo, é a famosa translação.
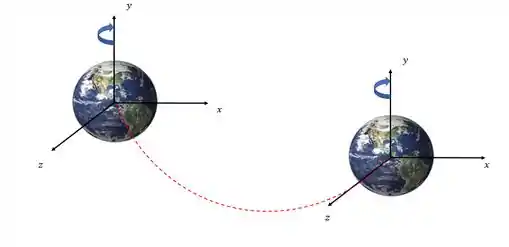
Em algum momento da sua vida, você talvez tenha ouvido que os planetas fazem o movimento de translação ao redor do Sol e de rotação ao redor do próprio eixo. E como calculamos a energia cinética de um planeta, então? Somando a parcela referente a translação com a parcela referente a rotação:
Conservação de Energia
Mas então, aprendemos que existe uma energia cinética de rotação que é usada quando os objetos rotacionam. Será que podemos usar isso, num caso de conservação de energia mecânica?
Vamos ver um exemplo:
A barra da figura abaixo possui massa e tamanho e é presa no nível do chão por uma de suas extremidades. A sua outra extremidade é abandonada e gira até a barra bater no chão. Qual é a velocidade linear da extremidade livre quando chega ao nível do solo? E qual sua velocidade angular no mesmo ponto?
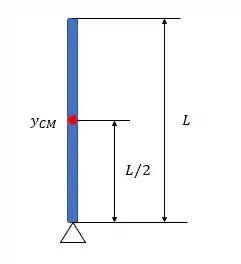
O problema é solucionado por conservação da energia mecânica.
Como no inicio a barra foi abandonada, sua velocidade inicial é zero, então só há energia potencial gravitacional e como a barra é um corpo extenso, levamos em conta os dados em relação ao seu centro de massa. Considerando o chão como o eixo de referência, teremos:
Já pra situação final a gente vai ter a barra no chão e sua velocidade angular final indicada na figura.
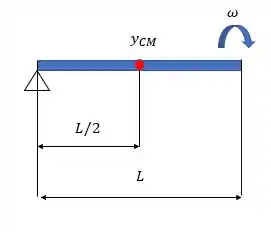
Teremos energia cinética rotacional, porque a barra estará girando em torno do seu eixo, não teremos cinética translacional pois esse eixo é fixo, ou seja, temos aqui uma rotação pura.
E não teremos energia potencial gravitacional, já que o centro de massa da barra estará na altura do chão, que é o nosso nível de referência. Logo:
Por se tratar de um corpo rígido a energia de rotação é:
Daí substituindo:
Agora é só conservar a energia e podemos encontrar a velocidade angular final da barra:
O momento de inércia de uma barra rotacionando ao redor de uma de suas extremidades é geralmente tabelado:
(em algumas tabelas, há apenas o momento de inércia da barra ao redor do centro de massa e você pode chegar no momento de inércia da barra ao redor da sua extremidade pelo teorema dos eixos paralelos).
Substituindo:
Cortando alguns termos:
Opa, encontramos o valor da velocidade angular da barra no instante que ela chega no chão. Mas também queremos encontrar a velocidade da sua extremidade livre:
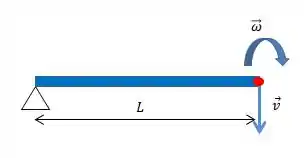
Lá da cinemática angular, conhecemos uma relação entre a velocidade linear de um ponto de um corpo e a velocidade angular desse corpo:
No nosso caso, a velocidade é a velocidade na extremidade da barra, é a velocidade angular da barra (que acabamos de encontrar) e é a distância do ponto até o eixo de rotação (que no nosso caso, é o comprimento da barra).
E como podemos ver no nosso desenho, quando a barra chega ao solo, essa velocidade na extremidade aponta para baixo.
E aí, bora praticar mais nos exercícios de fixação?
Conservação de Energia
Exercícios Resolvidos
Exercício Resolvido #1
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 287-33
Calcule o momento de inércia de uma roda que tem uma energia cinética de quando gira a .
Passo 1
Temos aqui um problema de aplicação direta da fórmula de energia cinética de rotação.
O valor do momento de inércia () é o que procuramos no problema.
Já o valor de deve ser convertido para , pois assim poderemos usar todas as unidades no Sistema Internacional, o padrão.
Passo 2
Reunindo as informações obtidas, temos:
Resposta
Exercício Resolvido #2
UFRJ-PF-2014.1-ME6
Uma esfera é lançada rolando sem deslizar subindo um plano inclinado com velocidade inicial do seu centro de massa. Um bloco é lançado subindo em translação um plano inclinado com a mesma inclinação e com a mesma velocidade inicial do seu centro de massa. No plano onde se encontra a esfera há atrito suficiente para que ela permaneça rolando sem deslizar e no plano onde está o bloco não há atrito.
A relação entre a altura máxima que o bloco atinge e a altura máxima que a esfera atinge nos respectivos planos é dada por
(a) , pois tanto a energia cinética do bloco como a da esfera se conserva.
(b) , pois tanto a energia mecânica do bloco como a da esfera se conserva.
(c) , pois o bloco desliza sem atrito.
(d) , pois a esfera rola sem deslizar.
(e) , pois tanto a energia mecânica do bloco como a da esfera se conserva.
Passo 1
Primeiro vamos determinar se a energia mecânica se conserva pro bloco e pra esfera.
Pro caso do bloco é fácil: não tem atrito (nem outra força não-conservativa) atuando, então ela se conserva.
Já pra esfera temos que ficar ligados! Tem atrito, mas se não tivesse a esfera não poderia rolar sem deslizar! Que nem provavelmente você já ouviu dizer que se o chão não tivesse atrito, não daria pra gente andar (por isso que pessoas que andam no gelo escorregam).
Enfim, o ponto é que esse atrito é só o suficiente pra esfera rolar sem deslizar, mas ele não faz a esfera perder energia!
Portanto, tanto a energia mecânica do bloco como a da esfera se conserva.
Passo 2
Apesar de na figura a esfera e o bloco não estarem exatamente no nível do chão, vamos considerar que eles partem com energia potencial gravitacional zero, ok?
Então a energia mecânica inicial deles é igual à energia cinética inicial associada à velocidade .
Passo 3
Começando pela esfera: vamos considerar que ela tem massa e raio .
Ela tem as energias cinéticas de rotação e de translação , então sua energia mecânica inicial é:
Passo 4
O momento de inércia de uma esfera de massa e raio é
E também temos a relação
Passo 5
Então a equação que achamos antes vai dar:
Então essa é a energia mecânica inicial da esfera!
Passo 6
Agora vamos supor que o bloco tem massa . Como vimos, sua energia mecânica inicial é igual à sua energia cinética inicial e vale
Passo 7
Agora vamos estudar as energias mecânicas finais da esfera e do bloco, começando pela esfera!
No fim do movimento, a esfera para numa altura : toda a sua energia cinética se transformou em energia potencial gravitacional, então:
Passo 8
E pela conservação da energia mecânica,
Multiplicando por dos 2 lados:
Passo 9
Da mesma forma, pro bloco,
e
Passo 10
Logo,
Passo 11
Recapitulando, achamos
Passo 12
Igualando as 2 expressões:
Chegamos nesse resultado por causa da conservação da energia mecânica, então a alternativa certa é a letra (e)!
Resposta
Alternativa (e)
Exercício Resolvido #3
UFRJ-P2-2014.1-M05
Um carro tem uma roda de massa e raio com momento de inércia relativo ao seu eixo de rotação que passa pelo seu centro de massa. O carro arranca em movimento retilíneo com a roda patinando na pista de modo que a velocidade de seu centrode massa esteja relacionada com sua velocidade angular de rotação por meio de . Nesse caso, a energia cinética da roda é
- ;
- ;
- ;
- ;
- ;
Passo 1
Nesse caso não podemos usar a fórmula da energia cinética onde calculamos o momento de inercia em relação ao centro de rotação. Isso porque não é nada fácil achar esse centro de rotação. Vamos fazer a fórmula separada
Passo 2
Começando pela energia cinética de rotação
Passo 3
A energia cinética de translação fica
Pelo enunciado
Então
Passo 4
A energia cinética total fica
Resposta
Letra E
Exercício Resolvido #4
Halliday, David, Fundamentos de física, volume I : mecânica, 8 ed. Rio de Janeiro : TLC, 2008, pp. 288-39
Na Fig. 10-36, duas partículas ambas de massa , estão ligadas uma à outra e a um eixo de rotação em por duas barras finas, ambas de comprimento e massa . O conjunto gira em torno do eixo de rotação com velocidade angular . Em relação a , quais são (a) o momento de inércia do conjunto e (b) a energia cinética do conjunto?
Passo 1
A primeira impressão que temos ao ver esse exercício é que é algo novo, que ainda não vimos, mas vamos olhar agora com mais calma.
Você aprendeu a calcular momento de inércia de um sistema de partículas, certo? Ah, se não aprendeu, não tem problema! Por que eu vou explicar rapidinho aqui!
Ok, temos duas partículas nesse exercício, e você vai fazer o mesmo: somar. Lembrando que o momento de inércia da partícula é dado por:
A parada é que agora temos duas barras, corpos extensos, pertencendo ao mesmo sistema da partícula. O que fazer?
É so somar também! E o momento de inércia da barra é dado por:
Só que no caso da nossa barra que é presa pela extremidade teremos que usar o teorema dos eixos paralelos.
Onde é a massa da barra e é a distância do centro de massa do corpo até o eixo de rotação.
Detalhe que só podemos somar esses momentos de inércia pois as partículas e os corpos rígidos formam um sistema que anda junto e rotaciona ao redor de um mesmo eixo, por isso,
para encontrar o momento de inércia do sistema só precisamos somar o momento de inércia de cada corpo em relação ao eixo de rotação.
Passo 2
a) Temos que fazer o momento de inércia do sistema que é a soma dos momentos de inércia:
Vamos identificar as partes do sistema e as suas distâncias ao eixo:
Portanto:
Para barra 1, temos uma barra presa por uma extremidade, então temos que usar o teorema dos eixos paralelos:
Já para a barra 2, precisamos fazer uso do teorema dos eixos paralelos de novo e aqui a distância do eixo é :
Já que temos todos os momentos de inércia vamos para o cálculo do momento de inércia do sistema.
Passo 3
Como o momento de inércia do sistema é a soma dos momentos de inércia de cada componente temos:
Passo 4
Agora com o momento de inércia do sistema, fica moleza para calcular a energia cinética de rotação:
Resposta
Exercício Resolvido #5
USP-P3-2015-8
Um poste cilindrico, fino e homogêneo de 10 metros de altura é derrubado, a partir da posição vertical. Sua base permanece fixa durante sua queda. Qual a velocidade da ponta do poste quando ele atinge o chão?(Despreze os atritos e dissipações neste caso.)
a)
b)
c)
d)
e)
Dados:
Momento de inércia de uma barra:
Passo 1
Típica questão de conservação de energia em corpos rígidos, não tem segredo, galera! O único cuidado que temos que ter é que temos que calcular tudo para o centro de massa.
Teremos inicialmente o seguinte caso:
Passo 2
Pela conservação da energia mecânica, teremos:
Como no início a barra está parada e como no final a barra está no chão, . Assim, teremos:
Como tudo o que temos que calcular tem que ser calculado pelo centro de massa, teremos:
Passo 3
Daí, temos que saber que é esse aí. Da tabela que ele dá no final da prova, ele nos diz que o momento de inércia no eixo de rotação da barra é dado por:
Pelo transferindo o eixo para a ponta, ou seja, arrastando L/2, pelo Teorema dos Eixos Paralelos, teremos:
Substituindo lá no Passo 2, vai ficar:
Substituindo lá:
Passo 4
Como ele quer a velocidade na ponta, é só usar...
Resposta
Letra E