Condutores e Isolantes
Teoria
Fala, pessoal. Estamos aqui hoje para falar um pouco sobre condutores e isolantes.
Nós classificamos os materiais em condutores ou isolantes de acordo com a capacidade que eles tem de permitir a passagem de corrente elétrica.
Mas calma, antes de mostrarmos de fato o que faz um material ser condutor ou isolante, vamos falar rapidamente sobre as cargas elétricas, porque isso vai ser importante para entender melhor esses dois tipos de materiais, combinado?
Existem quatro informações principais que precisamos saber sobre as cargas elétricas:
- Cargas elétricas podem ser positivas os negativas;
- Cargas de sinais iguais se repelem e cargas de sinais opostos se atraem;
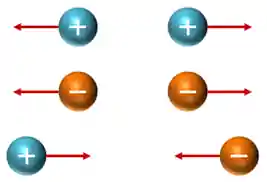
- Corpos ditos eletricamente neutros têm quantidades iguais de cargas positivas e negativas;
- Corpos ditos eletricamente carregados têm quantidades diferentes de cargas positivas e negativas.
Ok, agora que já sabemos o principal sobre as cargas elétricas, podemos avançar.
Condutores e Isolantes
A gente falou lá no início que classificamos os materiais em condutores e isolantes de acordo com a capacidade que os materiais tem de permitir a passagem de corrente elétrica. Cargas elétricas em movimento geram corrente elétrica, então, em outras palavras, podemos dizer que um material é dito condutor ou isolante de acordo com a facilidade com a qual as cargas elétricas se movem no seu interior.
Condutores
Um material é dito condutor quando as cargas elétricas se movem com muita facilidade em seu interior, ou seja, ele conduz a passagem de corrente elétrica.
Os metais (cobre, prata e ouro, por exemplo), a água da torneira e até mesmo o corpo humano são exemplos de materiais condutores. É por isso que quando a gente coloca a mão na tomada, por exemplo, a gente leva choque, porque como o nosso corpo é um condutor a corrente elétrica passa pela gente, irado não é?
Isolantes
Já os materiais isolantes são aqueles que promovem um efeito contrário dos condutores, ou seja, as cargas elétricas praticamente não conseguem se mover, é como se esse tipo de material isolasse a corrente elétrica.
Os pláticos, o vidro, a borracha e a madeira são exemplos de materiais isolantes.
Semicondutores
Existem ainda um tipo de material, que é chamado de semicondutor, porque ele é um meio termo entre o condutor e o isolante. Na verdade, esse tipo de material ele pode ser comportar como um condutor ou como um isolante dependendo das condições físicas. Digamos que ele é meio indeciso kkk.
O selênio e o germânio são exemplos de materiais semicondutores.
Comportamento das cargas elétricas nos materiais condutores e isolantes
Em um material condutor as cargas elétricas se distribuem apenas na superfície do objeto quando esse está no que chamamos de equilíbrio eletrostático. Por exemplo, se temos uma bola de metal, que é um material condutor, a carga elétrica estará distribuída na superfície desse objeto, desse jeitinho aqui:
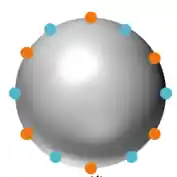
Agora, em materiais isolantes a carga elétrica ficará distribuida em todo o volume do objeto, desse jeito aqui:
Exercício
Topa fazer um exercício rapidinho aqui comigo para fixar esses conceitos que vimos hoje? Então, bora!
Identifique se a afirmação é verdadeira ou falsa:
I. Metais, em geral, são condutores de eletricidade, uma vez que permitem que cargas se movam com facilidade
II. São exemplos de materiais isolantes: isopor, borracha, vidro e cobre
III. Isolantes produzem efeito contrário de condutores, dificultando a passagem de corrente elétrica
RESOLUÇÃO
Vamos analisar uma alternativa de cada vez.
Alternativa I: Essa é VERDADEIRA. Vimos que os metais são mesmo um exemplo de materiais condutores
Alternativa II: Essa é FALSA. O isopor a borracha e o vidro são exemplos de materiais isolantes, mas o cobre é um metal e se comporta como um condutor.
Alternativa III: Essa é VERDADEIRA. Vimos exatamente isso hoje não é? Que os isolantes fazem o contrário dos condutores, dificultam a passagem de corrente elétrica.
Vídeo
Sim, nós temos esse conteúdo em vídeo também, então se você é daqueles que preferem assistir uma boa aula é só conferir aqui 👇🏾
Condutores e Isolantes
Comportamento das cargas elétricas nos materiais condutores e isolantes
Exercício
Vídeo
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Identifique se a afirmação é verdadeira ou falsa:
( ) Metais, em geral, são condutores de eletricidade, uma vez que permitem que cargas se movam com facilidade.
( ) São exemplos de materiais isolantes: isopor, borracha, vidro e cobre.
( ) Isolantes produzem efeito contrário de condutores, dificultando a passagem de corrente elétrica.
Passo 1
Bom, nessa primeira questão, temos que verificar algumas informações sobre os materiais condutores e isolantes. Vamos avaliar uma afirmação por vez.
Passo 2
“Metais, em geral, são condutores de eletricidade, uma vez que permitem que cargas se movam com facilidade”.
Como vimos, os condutores são materiais nos quais as cargas podem se locomover com facilidade e os metais são realmente um exemplo de materiais condutores. Essa afirmação, portanto, é verdadeira.
Passo 3
“São exemplos de materiais isolantes: isopor, borracha, vidro e cobre”.
Na teoria, nós vimos alguns exemplos de isolantes, entre eles: o isopor, a borracha e o vidro. O cobre, no entanto, é um exemplo de material condutor. Assim, essa afirmação é falsa.
Passo 4
“Isolantes produzem efeito contrário de condutores, dificultando a passagem de corrente elétrica”.
De fato, os isolantes são materiais nos quais as cargas têm muita dificuldade de se locomover, sendo que praticamente não há passagem de corrente elétrica. Então, essa afirmação é verdadeira.
Resposta
( V ) Metais, em geral, são condutores de eletricidade, uma vez que permitem que cargas se movam com facilidade.
( F ) São exemplos de materiais isolantes: isopor, borracha, vidro e cobre.
( V ) Isolantes produzem efeito contrário de condutores, dificultando a passagem de corrente elétrica.
Exercício Resolvido #2
Elaboração Própria
Uma esfera maciça de raio , composta por um certo material tem uma distribuição de cargas cuja função de densidade é à seguir:
Onde é a distância do centro da esfera até um ponto arbitrário.
Isto significa que as cargas estão distribuídas por todo seu volume, e que existem mais cargas próximas da superfície do que do centro.
Dado que a esfera está em equilíbrio eletrostático, determine se o material é isolante, condutor ou não importa.
Passo 1
Como a esfera está em equilíbrio eletrostático, temos duas opções:
- Ela é de material condutor, e todas as suas cargas deveriam estar na sua superfície;
- Ela é de material isolante, e suas cargas podem estar em qualquer lugar de seu volume.
Como a função de densidade mostra que existem cargas distribuídas por todo o volume da esfera, ela tem que necessariamente ser feita de material isolante.
Resposta
A esfera é composta por material isolante.
Exercício Resolvido #3
Elaboração própria.
Um determinado material possui, no equilíbrio eletrostático, uma distribuição de cargas uniformemente simétricas, porém não uniformes, possui uma densidade dada por:
e
em que é uma constante positiva. Dada essa distribuição, o material em questão seria condutor ou um isolante?
Passo 1
Bom, a primeira coisa que precisamos notar aqui é o comportamento da distribuição de carga com a distância . Quando , ou seja, exatamente no centro da esfera, vamos ter que
o que significa que o material que a gente está considerando tem carga no ponto . Além disso, se a gente vai aumentando a distância a partir do centro em direção à superfície do material, ainda teremos alguma carga até que, exatamente em , sendo R a nova distância do centro da esfera.
Como tem carga distribuída dentro do volume da esfera em e essa esfera está no regime eletrostático, então material não pode ser um condutor.
Sabemos que o condutor no equilíbrio eletrostático tem as cargas em excesso todas distribuídas sobre a sua superfície e, por isso, dentro do volume do condutor não há cargas. E, de fato, não poderia ser um condutor, pois em , temos , ou seja, não há carga sobre a superfície do material.
Por essa razão, o material que estamos analisando seria um isolante com cargas distribuídas ao longo de seu volume () e nenhuma carga sobre sua superfície ().
Resposta
O material em questão seria um isolante.
Exercício Resolvido #4
Elaboração própria.
Na Figura abaixo, temos uma esfera metálica, inicialmente neutra, conectada por um fio de náilon a um suporte. Em seguida, um bastão de plástico carregado negativamente é aproximado dessa esfera e conectado a ela por meio de um fio de cobre, sendo que este é mantido na direção horizontal com o auxílio de um outro fio de náilon, como mostra a Figura. A seguir, o fio de cobre é afastado para longe da esfera e do bastão. Sobre essa situação, são feitas as seguintes perguntas.
- Com o bastão negativo ainda perto da esfera metálica, a força entre a esfera e o bastão é de atração, repulsão ou não existe força entre eles? Explique.
- Se agora aproximamos um outro bastão, mas com carga positiva, como é a força entre a esfera e esse novo bastão?
Passo 1
a) Vamos lá? Esse é um típico problema em que podemos verificar a diferença entre condutores e isolantes. O cobre, como já comentamos na teoria, é um bom condutor e, por isso, as cargas fluem com facilidade nele. Por outro lado, o náilon não conduz cargas elétricas e por isso é um isolante.
Quando aproximamos a carga negativa do bastão e o conectamos à esfera metálica utilizando o fio de cobre, cargas negativas vão fluir facilmente pelo cobre e chegar à esfera metálica, que passará a ter uma carga também negativa. Blz?? Nenhuma carga negativa vai ser desviada para os fios de náilon, porque eles são isolantes e por isso é que são usados nesse caso.
Teremos, nessa nova situação, dois corpos com cargas negativas: o bastão e a esfera metálica. Por isso, após o fio de cobre ser retirado, existirá uma força de repulsão entre o bastão e a esfera. Tranquilo?
Passo 2
b) Se depois que retiramos o fio de cobre da jogada, aproximamos agora um objeto com carga positiva, então teremos uma atração entre a esfera, que tem carga negativa, e o bastão positivo.
Resposta
- A força será repulsiva;
- A força será atrativa.
Exercício Resolvido #5
ITA - SP
Duas esferas metálicas, A e B, de raios R e 3R, respectivamente, são postas em contato. Inicialmente A possui carga elétrica positiva e B carga . Após atingir o equilíbrio eletrostático, as novas cargas de A e B passam a ser, respectivamente:
Passo 1
Primeiro vamos nos organizar, temos:
Vamos chamar as novas cargas de A e B, respectivamente, de: e .
Passo 2
Agora temos que lembrar que as cargas irão se conservar, então:
Essa vai ser a nossa equação 1.
Passo 3
Agora precisamos encontrar uma outra equação para resolver o nosso sisteminha.
Essa segunda equação vai aparecer quando igualarmos o potencial das duas esferas:
Substiuindo os raios do enunciado
Que simplificando fica
Passo 4
Agora que temos as duas equações podemos resolver o nosso sistema.
Fazendo as devidas substituições em (2), vamos encontrar que:
Substituindo em (1), temos:
E...
Para encontrarmos o valor de , temos:
Portanto, a resposta correta será a letra (d)
Resposta
Exercício Resolvido #6
UFRJ, Física 3, P1 – 2011.2, Questão ME04
Temos um condutor oco, com carga Q, em equilíbrio eletrostático, conforme mostra a figura.
Com uma pequena esfera condutora, também de carga Q, considere as quatro seguintes situações:
(I) a esfera é colocada dentro da cavidade oca, sem tocar a superfície interna.
(II) a esfera é colocada dentro da cavidade, em contato com a superfície interna .
(III) a esfera é colocada em contato com a superfície externa do condutor oco.
(IV) a esfera é colocada na vizinhança (externa) do condutor oco, sem tocar nele.
Após atingido o equilíbrio eletrostático e referindo-se às cargas nas superfície interna e
externa do condutor oco como e , respectivamente, qual das alternativas corresponde
às quatro situações descritas anteriormente?
(a) I:
II:
III:
IV:
(b) I:
II:
III:
IV:
(c) I:
II:
III:
IV:
(d) I:
II:
III:
IV:
(e) I:
II:
III:
IV:
Passo 1
Bom, vamos por partes.
No ítem (I):
Se a pequena esfera no interior da cavidade tem carga Q, ela irá atrair cargas de sinal oposto para a superfície interna do condutor. Portanto .
Mas se o condutor esta carregado com uma carga Q, precisamos compensar essa carga da superfície interna com uma carga 2Q na superfície externa:
Entao...
Passo 2
No ítem (II):
Se a pequena esfera é colocada dentro da cavidade e em contato com o condutor, toda a carga da pequena esfera irá para o condutor e ficará na superfície externa deste. Lembra? Em um condutor em equilíbrio eletrostático as cargas se distribuem na superfície (externa).
Pensa da seguinte maneira, as cargas de mesmo sinal tendem a se repelir certo? Entao elas vao se colocar na posição em q cada uma esteja o mais afastada da outra, ou seja, na superfície. Entendeu? =)
Então...
Passo 3
No ítem (III):
Esse ítem é um pouquinho mais complicado, vamos precisar usar uma formula que aparece quando dois condutores de tamanhos diferentes são unidos.
Assim como no ítem anterior, não haverá carga na superfície interna do condutor.
Com relação a carga na superfície externa precisamos avaliar:
Lembra daquela formula da teoria ?
Vamos aplicar ele no problema:
Como o enunciado diz que a esfera é pequena, podemos supor que e rearranjando a equação acima temos:
E portanto
Ou seja, tem muito mais carga no condutor que na esfera pequena e podemos considerar que toda carga estará na superfície externa do condutor.
Então...
Passo 4
No ítem (IV):
Assim como nos dois ítens anteriores, não haverá carga na superfície interna do condutor.
Com relação a carga na superfície externa, podemos perceber que a carga do condutor continuará a ser Q e a da pequena esfera também continuará a ser Q. A única coisa que irá ocorrer é que as cargas das duas vão se repelir, se localizando com maior densidade na extremidade oposta à que está mais próxima uma da outra.
Então:
Passo 5
Podemos verificar que a resposta é a letra (c)
Resposta
(c) I:
II:
III:
IV: