Lei de Coulomb
Produzido por Bruno SoaresTeoria
A lei de Coulomb nos diz que a força eletrostática entre duas cargas elétricas é proporcional ao módulo das cargas elétricas e inversamente proporcional ao quadrado da distância que as separa.
Nesse vídeo abaixo, a gente explica tudo o que você precisa saber sobre Lei de Coulomb pra conseguir resolver qualquer exercício que aparecer na sua frente! 😉 👇
Ou continua comigo no textinho, e bora entender como funciona esse negócio de cargas elétricas!
Quando falamos de cargas e corpos elétricos existem dois princípios que são muito importantes:
- Cargas de mesmo sinal se repelem:
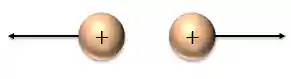
- Cargas de sinais opostos se atraem:
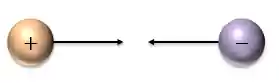
Essa atração ou repulsão ocorre porque existe uma força, que chamamos de força elétrica atuando sobre essas cargas. E a grande questão é:
Como calcular exatamente quanto vale essa força de atração ou de repulsão entre as cargas? E foi pra acabar com esse "problema" que surgiu a Lei de Coulomb.
Fórmula da Lei de Coulomb
Considere duas cargas puntiformes positivas que estão separadas por uma distância
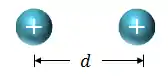
Existe uma força elétrica que atuará sobre cada uma dessas cargas e o módulo da força elétrica entre essas duas cargas
Onde:
é o módulo/intensidade da força elétrica, em Newton ; e são os módulos das cargas e , respectivamente, em Coulomb ; é a distância entre as cargas, em metros ; é a constante eletrostática. Ela é uma constante de proporcionalidade e depende do meio no qual as cargas estão. Quando estamos no vácuo o seu valor é esse aqui: .
E essa é a tal da Lei de Coulomb!
Opa! Mas estamos falando de uma força elétrica, que é uma grandeza vetorial, sendo assim, precisamos saber determinar também a sua direção e sentido.
A sua direção é a mesma da reta que liga os centros dos dois corpos em questão.
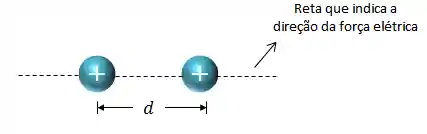
Já vimos que a força elétrica pode ser de atração (cargas de sinais opostos) ou de repulsão (cargas de mesmo sinal) e, assim sendo, para o nosso exemplo o seu sentido é dado conforme a figura abaixo:
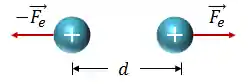
É importante a gente observar também que há uma força elétrica atuando em cada uma das cargas que estão interagindo, e como o módulo das cargas se mantém o mesmo, a força aplicada em ambas as cargas possuem o mesmo módulo , mas com sentidos opostos. Essa informação é importante, guarda no coração, combinado?
Podemos agora estender para interação entre duas cargas negativas e cargas diferentes. O módulo continuará sendo dado pela Lei de Coulomb e a direção e sentido serão como na figura abaixo:
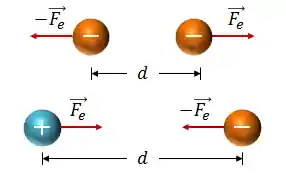
Observando a fórmula, podemos dizer que a força elétrica descrita pela Lei de Coulomb é:
- Diretamente proporcional às cargas dos corpos: se duplicarmos uma das cargas, duplicamos a força.
- Inversamente proporcional ao quadrado da distância entre as cargas: se duplicarmos a distância (ou seja, utilizarmos
ao invés de ), iremos dividir a força por .
Exercício Resolvido Passo a Passo
Topa fazer um exercício aqui comigo para fixar esse conceito? Então bora lá.
Dado a figura abaixo, calcule o vetor força elétrica que a partícula 1 faz na partícula 2 e o que a partícula 2 faz na partícula 1. Sabendo que as cargas são dadas por:
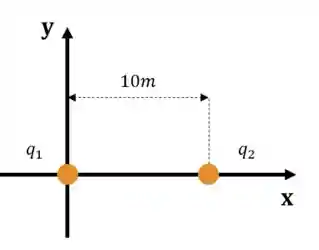
Passo 1: Aplicar a Lei de Coulomb
Primeira coisa que vamos fazer é aplicar a Lei de Coulomb para sabermos o módulo da força elétrica e, para isso precisamos organizar os dados que temos:
Sabendo esses dados, podemos aplicar a Lei de Coulomb:
Passo 2: Orientar as forças elétricas
Como as duas cargas são positivas as forças serão de repulsão. Então a força que 1 faz em 2 será da esquerda para direita (sentido positivo) e a força que 2 faz em 1 será da direta para esquerda (sentido negativo):
Prontinho! Agora que você sabe tudo de Lei de Coulomb, bora praticar com exercícios?
Fórmula da Lei de Coulomb
Exercício Resolvido Passo a Passo
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Dado um sistema isolado conforme discriminado abaixo:
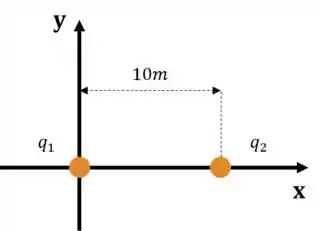
As cargas são dadas por: e .
Calcule o vetor força elétrica que a partícula 1 faz na 2 e o que a partícula 2 faz na 1.
Dado:
Passo 1
Aplicando a fórmula da força elétrica:
Substituindo os valores das cargas e da distância, podemos calcular o seu módulo:
Substituindo o valor de :
Passo 2
A partir daí, basta orientar a força de cada partícula. Como ambas tem a mesma carga, a força é repulsiva, ou seja, no sentido de afastar as duas.
Portanto, a carga vai fazer em uma força para a direita. Logo:
Ou, para quem gosta da outra notação, multiplicamos pelo vetor o módulo para que ele aponte na direção certa:
Passo 3
Pela mesma lógica, a partícula faz em uma força que aponta para a esquerda. Portanto:
Ou seja:
Sem fazer esse raciocínio, nós poderíamos também ter chegado à essa conclusão pela Lei de Newton da ação e reação.
Resposta
Exercício Resolvido #2
Elaboração Própria
Dada a configuração de cargas abaixo:
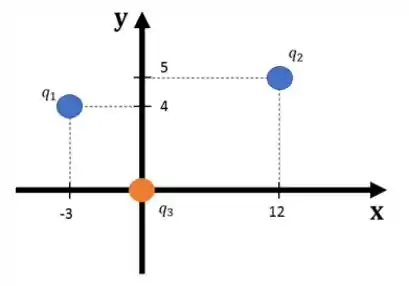
Onde:
Calcule a força resultante sobre a carga .
Passo 1
Para calcular a força resultante sobre a carga, basta somarmos todas as forças sendo exercidas nela, essa estratégia é conhecida também como superposição dos efeitos. Usaremos pra ambas as cargas a equação:
Onde é a direção da força entre a cargas e é o quadrado da distância entre elas. Vamos desenhar as distâncias das cargas até a carga
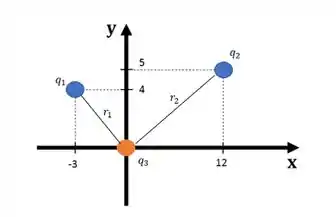
Então vamos começar calculando a força que faz em :
E encontramos a distância ao quadrado por Pitágoras:
Substituindo:
Passo 2
Agora precisamos achar o vetor unitário . É apenas um exercício de trigonometria. Sabemos que ele aponta de para :
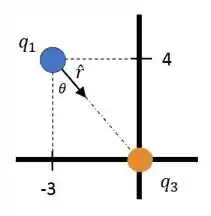
Decompondo, nós temos:
Agora temos:
Por consequência, obtemos:
Passo 3
Fazendo o mesmo processo para a interação entre as cargas 2 e 3:
Encontramos:
Portanto:
Passo 4
Buscamos agora encontrar o vetor que dá a direção da força que a carga 3 exerce em 2.
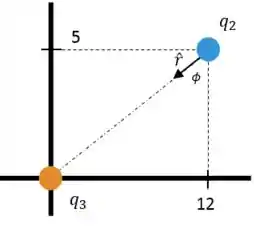
Temos:
Onde:
Portanto obtemos:
Passo 5
Para achar a força resultante, basta somar!
Não vamos nem brincar de arrumar isso aí, né? Ninguém merece.
O importante é você ter entendido a ideia.
Resposta
Exercício Resolvido #3
Hugh D. Young e Roger A. Freedman, Física III – Eletromagnetismo, 12ª ed. São Paulo, 2010, pp. 32
Três cargas puntiformes estão dispostas ao longo do eixo . A carga está na origem e a carga está em . A carga . Onde estará localizado quando a força resultante sobre for no sentido ?
Passo 1
Se tomarmos a liberdade de desenhar essa bagaça, vamos poder começar a entender melhor o problema:
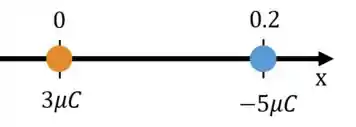
Lembrando que não precisa colocar o no desenho pois sua posição é desconhecida. Você pode até colocar, mas contanto que isso não te sugestione a pensar que a carga deve ficar necessariamente na parte positiva do eixo (que é o que 90% das pessoas fazem).
Podemos ver que, pelo sinal das cargas, a força em é atrativa e portanto aponta para a direita ().
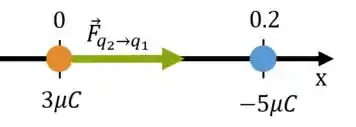
Passo 2
Do enunciado, sabemos que a resultante em é no sentido de , portanto:
Uma vez que tenhamos uma dessas forças, podemos calcular a outra.
Passo 3
Podemos aplicar a Lei de Coulomb para achar a força resultante em , onde nossa incógnita é a distância entre e , pois a posição de é desconhecida.
Plugando os valores, e sabendo que o vetor unitário (que aponta da carga que faz a força para aquela que sofre a força) no eixo é o nosso (menos xis chapéu).
Fazendo de cabeça:
Passo 4
Aplicando esse valor encontrado na equação da resultante:
Agora show. Como a carga e tem sinais opostos, sabemos que ela fazem uma força atrativa entre si. Logo, o único jeito dela fazer uma força atrativa no sentido de é estando na parte negativa do eixo :
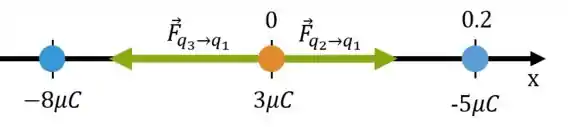
Se não se convenceu tente colocar ela em outra posição.
Passo 5
Aplicando a mesma lógica para as cargas e :
Neste caso, tratar com o módulo do vetor facilita nossa vida:
Sabendo que o é a nossa incógnita desejada:
Isolamos:
Plugamos os valores:
Como já conseguimos inferir que deve estar na parte negativa do eixo , substituímos:
Resposta
Exercício Resolvido #4
Hugh D. Young e Roger A. Freedman, Física III – Eletromagnetismo, 12ª ed. São Paulo, 2010, pp. 36
Duas esferas idênticas de massa estão suspensas em fios de seda (??) de comprimento , como indicado na figura abaixo. Cada esfera possui a mesma carga; logo, . O raio de cada esfera é muito pequeno em comparação à distância entre as esferas, de modo que elas podem ser consideradas cargas puntiformes. Mostre que, se o ângulo for pequeno, a distância no equilíbrio entre as esferas será dada por .
Sugestão: quando for pequeno, então
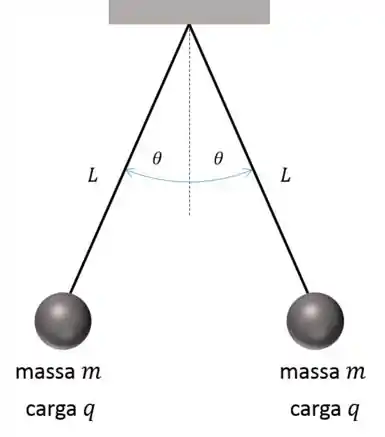
Passo 1
Belezinha. Questão que remete à Física I, a parada é fazer as equações do equilíbrio para as esferas:
Na realidade, por causa da simetria só precisa fazer as equações pra uma delas. Então partiu.
Decompondo para a esfera da esquerda:
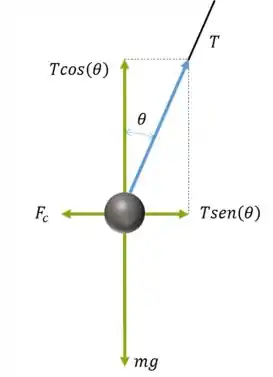
Temos que as equações são:
A brincadeira é resolver para a distância entre as esferas, que ainda não apareceu na equação. Ainda tem uma incógnita que não tratamos, que é a força repulsiva entre as esferas.
Passo 2
Sabemos também que a força entre as esferas é dada pela equação de Coulomb:
Substituindo:
Agora falta se livrar dessa tensão, que não é dado.
Passo 3
Usando a equação do equilíbrio em , temos:
Substituindo:
Arrumando a bagunça:
Agora é a hora de usar o dado do enunciado!
Passo 4
Como foi dado que, para pequeno temos:
Tiramos da figura o seno:
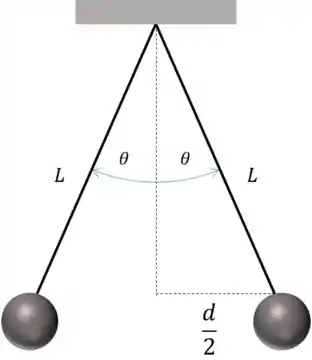
Substituindo na equação:
Agora é só isolar o :
Substituindo o valor de :
Temos que:
E fim de papo. O resto é só tirar a raiz:
Resposta
Ei, a resposta está no passo a passo :)
Exercício Resolvido #5
UFRJ-P1-2014.2-Múltipla Escolha n°1
Considere um quadrado, com aresta de comprimento , com partículas em todos os seus 4 vértices, conforme mostra a figura.
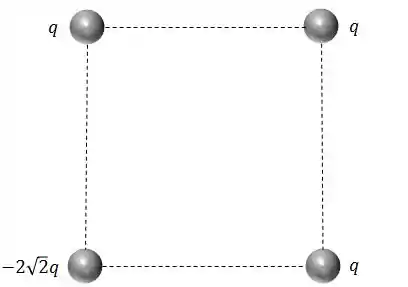
Qual é o módulo da força elétrica resultante sobre a partícula no vértice superior direito?
Passo 1
Beleza, vamos começar calculando o vetor força elétrica resultante sobre a partícula no vértice superior direito. Pra isso, vamos calcular, separadamente, as forças que cada outra partícula faz sobre a partícula que estamos interessados.
Lembrando que a força elétrica entre duas cargas é dada por:
Vamos começar numerando as cargas pra não nos enrolarmos:
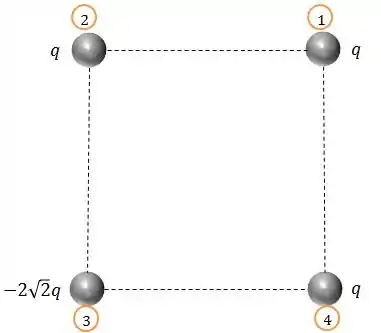
Levando em consideração os sinais das cargas, as forças terão os seguintes sentidos:
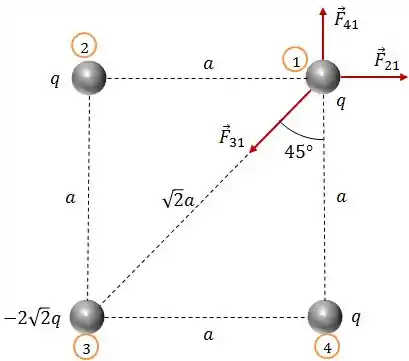
Agora já podemos começar a escrever as forças elétricas.
Passo 2
- Força elétrica de 2 sobre 1:
- Força elétrica de 4 sobre 1:
- Força elétrica de 3 sobre 1:
Finalmente, o vetor força resultante sobre a carga 1 será:
A resposta certa é a letra .
Resposta
Exercício Resolvido #6
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Exercício 21.22, pp. 32.
Duas cargas puntiformes positivas estão localizadas sobre o eixo sobre os pontos e . Uma outra carga puntiforme negativa está localizada em algum ponto sobre o eixo .
- Faça um diagrama de corpo livre mostrando as forças que atuam sobre a carga ;
- Encontre as componentes e da força resultante da ação das duas cargas positivas sobre . (Sua resposta deve envolver somente , , , e a coordenada da terceira carga.)
- Qual é a força resultante sobre a carga quando ela está na origem ()?
Passo 1
a) O que a gente tem neste exercício está mostrado na figura abaixo. Como as cargas são positivas, a carga negativa , que está na posição sobre o eixo , sente uma força de aproximação na direção da linha que une e as cargas positivas , como desenho para você abaixo.
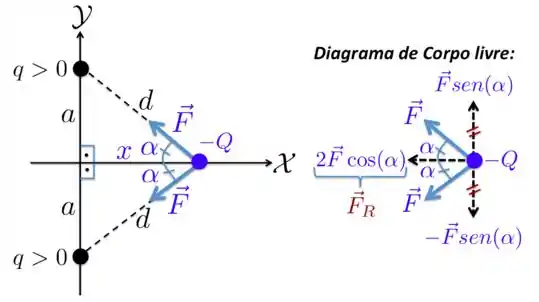
Fazer um diagrama de corpo livre aqui significa isolar a carga de interesse, no caso , e representar as forças que agem sobre ela, tipo o que mostramos na figura à direita acima!!! Como as forças são de atração e fazem um ângulo com o eixo , elas têm componentes tanto na direção , quanto na direção .
Passo 2
b) A gente vê que as componentes na direção se cancelam porque elas têm o mesmo módulo, a mesma direção, porém sentidos diferentes, por isso se cancelam. Então, na direção , o módulo força resultante é nulo:
Então, a gente só precisa mesmo olhar para as componentes sobre o eixo da força resultante. A soma das componentes em dará a força resultante . Essa força resultante será, então,
Sabemos que a intensidade da força entre e é dada pela lei de Coulomb, que é
Agora, dá uma olhada lá na figura para o triângulo retângulo. Olhou? Mesmo? Rsrs... Desse triângulo, podemos escrever que
Com as duas últimas expressões, conseguimos representar o móduloda força resultante como
e essa é a componente da força resultante: . Representando em termos de vetores
ou seja, a força resultante tem componente na direção , como mostramos para você lá na figura.
Passo 3
c) Para fechar o exercício, dá uma olhada na expressão para o vetor força resultante que acabamos de encontrar. Se você joga nessa expressão, obtém que
Sem fazer conta, para a gente checar se esse resultado tá ok ou não, imagina que a carga negativa está na origem. Nessa posição, as forças, devidas às cargas positivas , têm o mesmo módulo, mesma direção, porém sentidos contrários, já que as cargas estão à mesma distância da origem .
Isso significa que, em , realmente temos
Então fechou, a nossa conta tá correta...\0/
Resposta
- Diagrama de corpo livre representado na figura;
Exercício Resolvido #7
Sears & Zemansky, Young & Freedman, Física III, Eletromagnetismo, Volume 3, 12˚ ed., São Paulo: Addison Wesley, 2009, Problema 21.78, pp. 37.
Duas cargas puntiformes e são mantidas fixas a uma distância de . Uma carga , de massa igual a , está inicialmente localizada a de cada uma dessas cargas, como mostra a figura abaixo e é libertada do repouso. Você verifica que a aceleração inicial de é da esquerda para a direita, paralela à linha que liga as duas cargas puntiformes. Dada essa situação, encontre os valores de e .
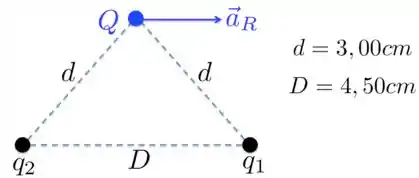
Passo 1
Neste exercício, a gente precisa descobrir primeiro para onde está apontando a força resultante . A gente sabe que está apontando na direção e sentido da aceleração , pois, a partir da segunda Lei de Newton, temos o seguinte:
sendo a massa da partícula carregada negativamente . Isso está representado no figura abaixo. Aqui não vai entrar a força peso pois é como se as cargas estivessem todas no mesmo plano, então não vai ter ação da gravidade, beleza?
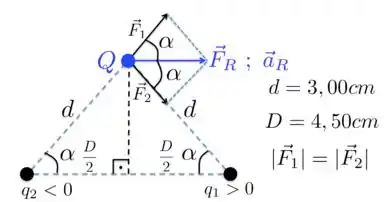
Também dessa figura, você consegue perceber que a carga deve ser negativa e a positiva, pois a soma vetorial tem que resultar em um vetor apontando na direção e sentido da aceleração resultante .
Além disso, como a força resultante é paralela a linha que une as cargas e , o módulo das forças e devem ser iguais, ou seja, devemos ter que
que representamos na figura também. Isso também significa que temos também , tranquilo?? Ou seja, essas duas cargas tem sinais contrários e mesmo módulo!
Um aspecto que é importante você reparar é o seguinte: a força resultante que vamos considerar é a força inicial no instante inicial em que a carga é liberada, porque depois desse instante, a força muda de valor, já que a distância entre e as outras cargas vai mudar e, consequentemente, a aceleração também vai ser outra. Blz? Por isso o exercício tomou o cuidado de dizer aceleração inicial no ponto onde a carga negativa está.
Passo 2
Mas, então, como fica o módulo da força resultante nesse caso? Lá da figura, você percebe que, colocando junto com a segunda Lei de Newton, o módulo da força resultante é igual a
Agora, usando um pouco de trigonometria, a gente vê que
Substituindo na expressão acima e isolando a carga , temos
Colocando os valores fornecidos pelo enunciado, obtemos que
o que nos mostra que
Resposta
Exercício Resolvido #8
UFRJ- Física 3 - PF 2017.2 - DIURNO - 1
Uma partícula está rodeada por partículas carregadas situadas em dois anéis concêntricos a ela, conforma mostrado na figura abaixo. Todas as partículas estão fixas em suas posições e suas cargas são indicadas na figura. Os raios dos anéis interno e externo valem e , respectivamente. Utilizando o sistema de coordenadas indicado, qual é a força eletrostática resultante sobre a partícula de carga ?
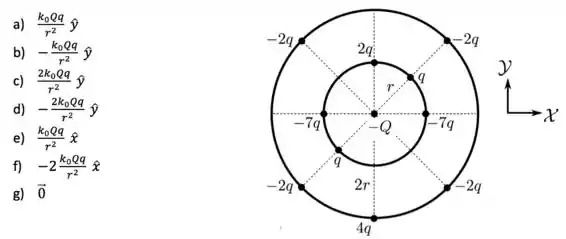
Passo 1
Esse tanto de cargas assusta e pensar que teríamos que fazer a conta de todas as forças sobre a carga já cansa a gente, não é mesmo? Na verdade, não precisamos fazer toda essa contaiada se percebemos que um monte dessas forças se cancelam aos pares \0/. Dá uma olhada na figura abaixo e na correspondência entre pares de cargas circuladas com o mesma cor.
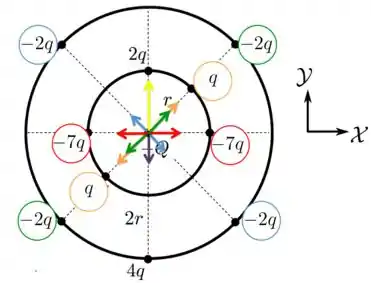
Todas os círculos com mesma cor mostram os pares de carga que dão origem a forças sobre a carga de mesma intensidade, mesma direção, porém sentido contrário e, por isso, se cancelam. As forças sobre são representadas pelos vetores situados no centro onde está .
Os únicos vetores que não se cancelam são os de cor amarela e roxa na direção do eixo que, apesar de estarem na mesma direção e terem sentidos contrários, não possuem o mesmo módulo como no caso das outras forças analisadas. Eles se referem a forças de atração devidas às cargas e que estão, respectivamente, a uma distância e de .
Portanto, basta calcular essas duas forças e partir para o abraço...\0/
Passo 2
A força em devida à carga (vetor em amarelo na figura acima) está na direção e é dada por
A força em devida à carga (vetor em roxo na figura acima) também está na direção , mas aponta para o sentido negativo do eixo e é dada por
Passo 3
A resultante das forças sobre é, portanto, a soma vetorial abaixo
SUGESTÃO: em questões com várias cargas estáticas em distribuições simétricas como as desse problema (que só precisamos calcular apenas duas forças e somá-las!!), procure sempre verificar se existem pares de cargas contribuindo com parcelas que se cancelam, pois isso pode te ajudar a ganhar tempo na solução do problema. Se liga nisso, OK? ;-).
Resposta
Portanto, a letra a) é a resposta correta.