Equilíbrio Estático em Pilhas de Tijolos
Teoria
Equilíbrio Estático em Pilhas de Tijolos
Vamos falar agora de um exercício típico em que é abordado o equilíbrio estático em pilhas de tijolos.
Geralmente, é pedido para achar a distância máxima, como mostra a figura, que garante que a pilha de tijolos, de comprimento e uniformes, esteja em equilíbrio.
Show! Como achamos esse ?
Como o objetivo da questão é achar o valor máximo de para estar em equilíbrio estático, vamos decompor a força peso do bloco de cima e ver como ela atua.
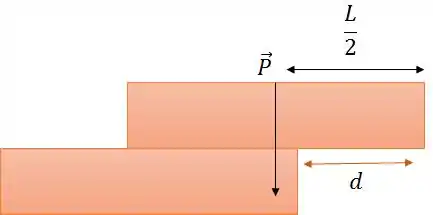
Nesse caso, como o tijolo é uniforme, o centro de massa do tijolo de cima é , certo? É o ponto que concentra todas suas forças.
Já que queremos o máximo, vamos aumenta-lo gradativamente.
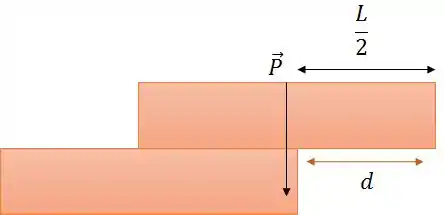
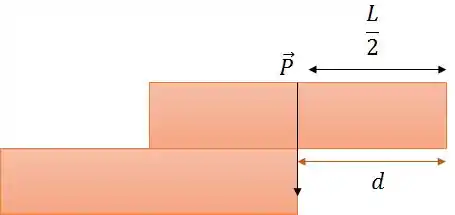
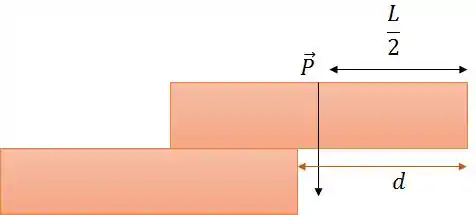
Ops! Percebeu o que aconteceu?
O peso do bloco de cima, concentrado em seu centro de massa, produz um torque no sentido horário que provoca o desequilíbrio dos blocos.
O bloco de cima vai girar!
Então, afinal, qual o valor máximo de ?
O valor máximo de é justamente encontrado quando o centro de massa passa pelo eixo de rotação, ou seja, a quina do bloco de baixo e está na iminência de girar.
Perceba:
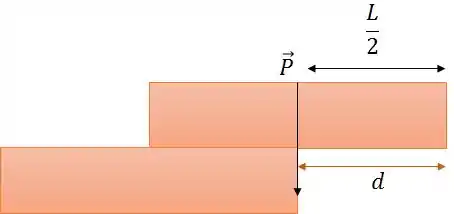
Nesse ponto, é máximo, já que a força não faz o bloco girar. Qualquer aumentozinho que você fizer em , a força vai gerar o torque.
Então, para descobrirmos o máximo, precisamos achar o centro de massa do bloco que está acima.
Em algumas ocasiões, precisaremos achar o centro de massa de dois ou mais blocos juntos.
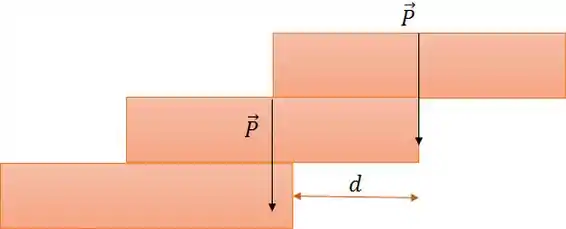
A figura acima retrata isso. Repare que a distância máxima vai ser encontrada no ponto do centro de massa dos dois blocos de cima.
Então precisamos calcular o centro de massa, usando a fórmula:
Aqui temos um macete. A dica é montar o eixo na extremidade do bloco do meio, ou seja, onde começa a distância , orientando o x positivo para a esquerda.
Dessa forma, o valor que você encontrar para o ponto do centro de massa, já será o valor máximo.
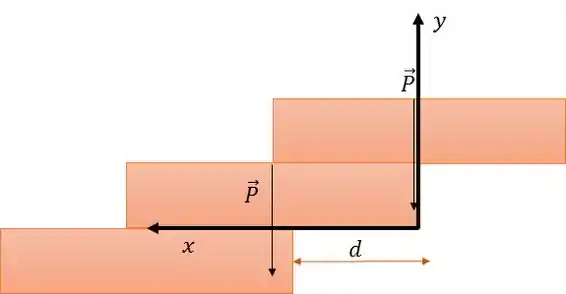
Assim, basta aplicar a fórmula de centro de massa dos dois blocos juntos que já achamos o máximo.
Outra coisa que é importante ter atenção.
Independentemente do número de tijolos que formarem a pilha, devemos começar sempre pelo primeiro. Isso deixa a resolução bem mais simples.
No primeiro caso, só teremos um bloco para analisar e assim vai aumentando conforme vamos analisando os blocos abaixo.
Então, é isso:
- Comece pelos blocos de cima
- Ache o centro de massa individual do ou dos blocos que estão sendo analisados
- Aplique a fórmula de centro de massa com o eixo orientado positivamente para o lado esquerdo e ache, assim, o centro de massa dos blocos em conjunto.
Não tem mistério! Vamos para os exercícios?
Exercícios Resolvidos
Exercício Resolvido #1
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 12, pp 24-59
Quatro tijolos de comprimento L, idênticos e uniformes, são empilhados (figura abaixo) de tal forma que parte de cada um se estende além da superfície na qual está apoiado. Determine, em termos de L, os valores máximos para que a pilha esteja em equilíbrio de:
Passo 1
Vamos analisar, primeiramente, .
O centro de massa do bloco mais de cima é , já que ele é uniforme. Logo, percebemos que o valor máximo pode ter é .
Perceba que se for maior que , o peso do bloco concentrado em seu centro de massa fará o bloco de cima girar no sentido horário.
Passo 2
Agora, vamos analisar o .
A situação é a seguinte:
Perceba que o máximo vai ser obtido quando a força concentrada dos pesos do bloco de cima e do bloco do meio atuar no eixo de rotação.
Repare que, se a situação fosse a essa:
A força concentrada dos dois blocos causaria uma rotação, e os blocos não estariam em equilíbrio.
=
Logo, precisamos saber qual o ponto dessa força concentrada.
Como as duas forças são iguais, vai estar na metade da distância entre as duas.
Passo 3
Mantendo a lógica, devemos achar o ponto em que as forças dos três blocos estão concentradas.
Para descobrirmos esse ponto, devemos calcular o centro de massa dos três blocos.
Podemos definir o eixo passando pela força com seu eixo x positivo orientado para a esquerda e aplicar a fórmula de centro de massa:
Agora, aplicamos a fórmula de centro de massa.
, sendo a massa de cada tijolo.
O momento gerado por é nulo, já que passa pelo eixo.
Resta então o momento de :
Como é o centro de massa dos três blocos de cima, . Perceba que se fosse maior que isso, a força concentrada dos três blocos estaria à direita do eixo de rotação e geraria torque nos blocos.
Passo 4
d) Para achar o raciocínio é o mesmo. Vamos achar o centro de massa dos 4 blocos juntos e já sabemos que o máximo vai ser o ponto em que a força concentrada dos quatro blocos atua.
Para aplicar a fórmula do centro de massa, vamos definir o eixo de rotação no ponto onde atua a força com seu eixo x positivo orientado para a esquerda:
Aplicamos, então, a fórmula de centro de massa:
, sendo a massa de cada tijolo.
O momento gerado por é nulo, já que passa pelo eixo.
Resta então o momento de :
Como o centro de massa é no ponto , o valor máximo de é .
Perceba que se fosse maior que isso, a força concentrada dos quatro blocos estaria à direita do eixo de rotação e geraria torque nos blocos.
Passo 5
máximo vai ser igual a soma de .
Resposta
Exercício Resolvido #2
Halliday e Resnick, Fundamentos de Física, Volume 2, 8ª edição, Cap 12, pp 25-75
Quatro tijolos iguais e uniformes, de comprimento L, estão empilhados em uma mesa de duas formas como mostra a figura abaixo. Estamos interessados em maximizar a distância nas duas configurações. Determine as distâncias ótimas , , e e calcule para os dois arranjos.
Passo 1
Vamos analisar primeiro o valor de .
Percebemos que o valor máximo de é no ponto em que o centro de massa do bloco da direita corta o eixo de rotação.
Repare que se fosse maior do que isso, os blocos não ficariam em equilíbrio e tenderiam a rotacionar.
Logo, precisamos saber o centro de massa do bloco da direita. Como é um bloco uniforme, seu centro de massa é .
Passo 2
Vamos analisar o agora.
A situação é a seguinte
Como no item anterior, precisamos achar o centro de massa dos quatro blocos juntos para descobrirmos o valor máximo de .
Podemos definir o eixo passando pela força do bloco da direita com seu eixo x positivo orientado para a esquerda.
Podemos agora aplicar a fórmula de centro de massa.
, sendo a massa de cada tijolo.
O momento gerado por da direita é nulo, já que passa pelo eixo.
Resta então o momento de e o momento do bloco do meio
Como é o centro de massa dos quatro blocos de cima, . Perceba que se fosse maior que isso, a força concentrada dos quatro blocos estaria à direita do eixo de rotação e geraria torque nos blocos.
Passo 3
para o caso 1 será dado pela soma de com
Passo 4
Vamos analisar agora a situação b. Seguiremos a mesma lógica apresentada anteriormente.
Como é simétrico, podemos achar o centro de massa dos dois blocos da direita e assim descobrirmos o valor máximo de .
Dividimos o peso do bloco do topo em duas forças para baixo, que na situação extrema se encontram na quina dos blocos do meio com valor de como mostra a figura. Repare que é a situação em que o centro de massa será mais distante da extremidade direita, o que nos dará o máximo.
Agora, precisamos achar o ponto de centro de massa dos dois blocos.
Podemos definir o eixo passando pela extremidade do bloco da direita com seu eixo x positivo orientado para a esquerda.
Podemos agora aplicar a fórmula de centro de massa.
, sendo a massa de cada tijolo.
Resta então o momento de e o momento do bloco da direita
Como é o centro de massa dos dois blocos (de cima e da direita), . Perceba que se fosse maior que isso, a força concentrada dos dois blocos estaria à direita do eixo de rotação e geraria torque nos blocos.
Passo 5
Vamos analisar agora .
Precisamos, da mesma forma, achar o ponto do centro de massa do quatro blocos juntos. Esse será o valor máximo de .
Pela simetria, é possível perceber que o centro de massa passa justamente no meio do bloco de baixo. Logo, .
Perceba que se fosse maior, os blocos tenderiam a girar para o lado direito e não estaria em equilíbrio estático.
Logo, o valor máximo de é justamente .
Passo 6
Falta agora só calcular que é a soma de e .