Enunciado
Física - Young and Freedman - Vol 4- Ed: 12º - Capítulo 36.Exercícios - Ex. 18
18. Considere uma figura de difração de fenda única em que a amplitude da onda no ponto mostrado na Figura é . Para cada um dos seguintes casos, desenhe um diagrama de fasores como o da Figura e determine graficamente a amplitude da onda no ponto em questão. (Sugestão: use a Equação para determinar o valor de em cada caso.) Calcule a intensidade e compare com a Equação . ; ; .
Passo 1
Então galera, para fazer o diagrama de fasores pedido no enunciado, temos que fazer primeiro a sugestão do enunciado de calcular o , porque ele é o elemento chave para fazer o diagrama como o da figura .
Para calcular vamos usar a seguinte fórmula, temos:
A figura vai nos ajudar bastante a ver como encontrar graficamente.
E para encontrar a intensidade a parti da amplitude, temos que lembrar do fato da intensidade ser proporcional a amplitude ao quadrado, então teremos que elevar a amplitude que encontramos ao quadrado e comparar com o resultado a parti da equação .
Passo 2
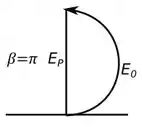
Vamos começar com o item , para esse caso temos , assim temos que:
Olhando a figura , temos que para um , nosso diagrama de fasores fica:
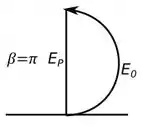
Se liga no seguinte, olhando a figura vemos que é igual a metade de uma circunferência com diâmetro , então usando a fórmula do comprimento da circunferência, temos:
Isolando , temos:
Elevando isso ao quadrado temos:
Usando a equação , temos:
Então o que encontramos está de acordo com a equação .
Passo 3
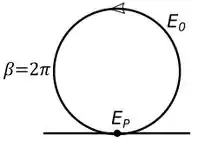
Vamos agora com o item , para esse caso temos , assim temos que:
Olhando a figura , temos que para um , nosso diagrama de fasores fica:
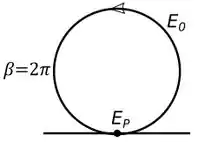
Se liga no seguinte, é a distância do começo do fasor até o final dele, mas como ficamos com um círculo fechado, logo:
Elevando isso ao quadrado temos:
Usando a equação , temos:
Então o que encontramos está de acordo com a equação .
Passo 4
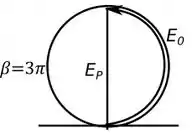
Vamos agora com o item , para esse caso temos , assim temos que:
Olhando a figura , temos que para um , nosso diagrama de fasores fica:
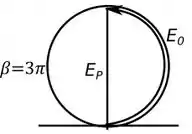
Se liga no seguinte, olhando a figura vemos que no total é uma circunferência e meia com diâmetro , então usando a fórmula do comprimento da circunferência, temos:
Isolando , temos:
Elevando isso ao quadrado temos:
Usando a equação , temos:
Então o que encontramos está de acordo com a equação .
Resposta
