Em um experimento, o campo elétrico é medido em pontos a distâncias de um fio retilíneo uniformemente carregado, que possui carga por unidade de comprimento e comprimento , em que . Em um segundo experimento, o campo elétrico é medido em pontos a distâncias do centro de uma esfera isolante uniformemente carregada, que possui densidade volumétrica de carga e raio , em que . Os resultados das duas medições são listados em uma tabela, mas você não é informado qual conjunto de dados se aplica a cada experimento:

Para cada conjunto de dados, desenhe dois gráficos: um para em função de e outro para em função de . Use esses gráficos para determinar qual conjunto de dados, ou , é para fio retilíneo uniformemente carregado e qual conjunto é para a esfera uniformemente carregada. Explique seu raciocínio. Use os gráficos da parte para calcular para o fio retilíneo uniformemente carregado e para a esfera uniformemente carregada.

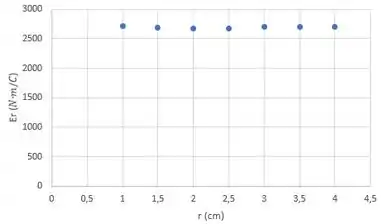
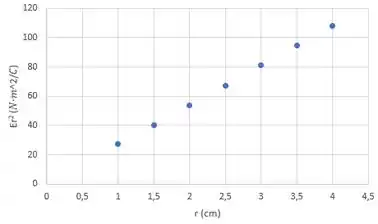
Os gráficos da medida são os seguintes:

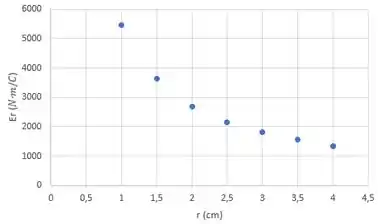
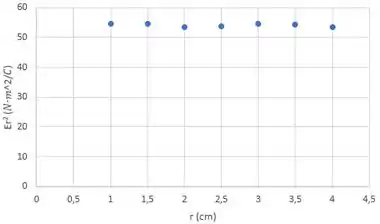
Agora os gráficos da medida .

Agora que temos os gráficos podemos descobrir qual medida se refere ao fio e qual se refere a esfera.

A equação do campo elétrico do fio é dada por:

Isolando , temos que:

Então o gráfico de referente ao fio deve ser constante e isso corresponde a medida .

A equação do campo da esfera é dada por:

Isolando , temos que:

Então o gráfico de referente a esfera deve ser constante e isso corresponde a medida .

Agora vamos para o item .

Ele quer que encontremos a densidade linear e a densidade volumétrica . Vamos começar com .

Isolando na equação do campo elétrico, temos:

Pegando um valor de do gráfico (vamos usar ), e substituindo o valor de , temos:

Agora para achar o ,vamos primeiro isolar na equação do campo da esfera, já que:

Onde é o volume da esfera. Então temos o seguinte:

Pegando um valor de do gráfico (vamos usar ), e substituindo o valor de , temos:

Agora podemos encontrar a densidade, temos:

Substituindo os valores, temos:

Finalizamos a questão com sucesso!