Enunciado
Física - Young and Freedman - Vol 3- Ed: 12º - Capítulo 28.Problemas - Ex. 69
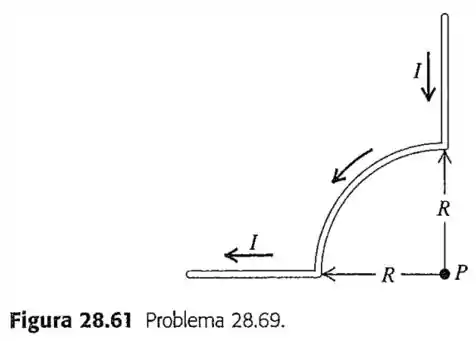
69- O fio na Figura conduz uma corrente no sentido indicado. O fio é constituído por uma seção retilínea longa, uma seção correspondente a um quarto de circunferência e outra seção retilínea longa. Calcule o módulo, a direção e o sentido do campo magnético resultante no centro de curvatura da seção correspondente a um quarto de circunferência (ponto ).
Passo 1
Por estarem na mesma reta que as seções retas podemos dizer que a contribuição de campo magnético das seções retas é nulo, pois a a parte vetorial de :
Será nula (melhor exercício para isso é o exercício desse capítulo, olha lá)
Já a contribuição do campo magnético da espira circular será de:
E será um campo que sairá da página. E também o campo total em .
Resposta
Exercícios de Livros Relacionados
A figura 29-79 mostra uma seção reta de um condutor cilíndrico longo de raio a = 4,00c m que contrém um furo cilíndrico de raio b = 1,50c m . Os eixos centrais do cilindro e do furo são paralelos e es
Um condutor longo, oco, cilíndrico (raio interno 2,0m m , raio externo 4,0m m ) é percorrido por uma corrente de 24A . A distribuição uniformemente na seção reta. Um fio longo e fino coaxial com o cil
Um condutor longo, oco, cilíndrico (raio interno 2,0m m , raio externo 4,0m m ) é percorrido por uma corrente de 24A . A distribuição uniformemente na seção reta. Um fio longo e fino coaxial com o cil
A figura 29-86 mostra uma seção reta de um condutor cilíndrico oco de raios a e b que conduz uma corrente i uniformemente distribuída. (a) Mostre que, no intervalo bra , o módulo B ( r ) do campo elét
A figura 29-87 mostra uma seção reta de um cabo coaxial longo de raios a , b e c . Corrente i de mesmo valor e sentidos opostos estõ uniformemente distribuídas nos dois condutores. Escreva expressões