Exercícios de Lei de Ampère - Lista de Exercícios Resolvida
Questão 1
Considere as seguintes afirmações:
- O campo magnético de uma espira circular por onde passa uma corrente estacionária satisfaz a lei de Ampère.
- A afirmação é verdadeira devido à simetria axial da espira.
- Se a espira fosse quadrada, a lei de Ampère não seria válida.
- Se a espira fosse quadrada, a lei de Ampère seria válida, desde que se escolhessem curvas amperiana que passassem pelo centro do quadrado.
São verdadeiras as afirmativas:
Somente
e
, e
e
Somente
Ver solução completaQuestão 2
Por um condutor cilíndrico maciço e infinito de raio passa uma corrente estacionária e axial uniformemente distribuída através de sua seção reta. O campo magnético a uma distância radial do eixo do condutor, em coordenadas cilíndricas , é igual a
e .
e .
e .
e .
e .
Ver solução completaQuestão 3
Um fio cilíndrico de raio transporta uma corrente uniformemente distribuída por sua seção reta e com sentido saindo do papel.
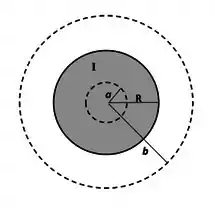
Encontre os raios das espiras amperianas circulares centradas no eixo do fio para as quais o campo magnético gerado pelo fio é dado por:
Ver solução completaQuestão 4
Determine a circulação para as três curvas fechadas orientadas respectivamente.
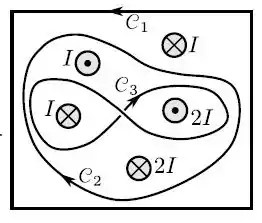
- pois todas são perpendiculares.
Questão 5
A figura a seguir mostra a seção reta de três fios que conduzem correntes estacionárias, com intensidade de mesmo módulo , que atravessam o plano da figura com sentidos indicados na mesma.
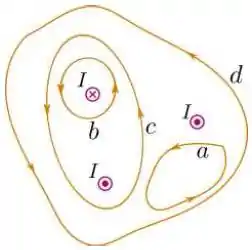
Quatro curvas orientadas indicadas pelas letras até são apresentadas na figura. A alternativa a seguir que melhor relaciona a circulação do campo magnético em cada curva é
.
.
.
.
.
Ver solução completaQuestão 6
Considere o cabo coaxial muito longo da figura ao lado, formado por duas cascas cilíndricas concêntricas com raios internos , e raios externos , , respectivamente. Uma corrente uniforme flui na casca cilíndrica interna com o sentido para fora do plano do papel e uma corrente uniforme com sentido desconhecido flui na casca cilíndrica externa.
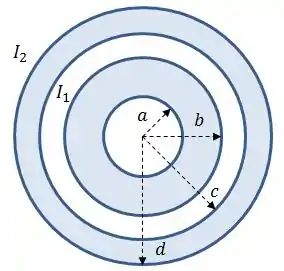
Calcule a intensidade do campo magnético nas regiões:
;
;
;
Sabendo que e que a amplitude do campo magnético em tem o valor de , calcule o valor da corrente em função da corrente , indicando seu sentido.
Calcule a amplitude do campo magnético em em função da corrente .
Ver solução completaQuestão 7
Um cilindro comprido, com seu eixo orientado ao longo do eixo , possui uma densidade de corrente . A densidade de corrente, embora seja simétrica em relação ao eixo do cilindro, não é constante e varia de acordo com a relação:
para
, para
onde é o raio do cilindro, é a distância radial entre o ponto considerado e o eixo do cilindro e é uma constante dada em ampères.
(a) Mostre que é a corrente total que passa através da seção reta do fio.
(b) Usando a lei de Ampère, deduza uma expressão para o módulo do campo magnético na região .
(c) Obtenha uma expressão para a corrente contida em uma seção reta circular de raio e centralizada sobre o eixo do cilindro.
(d) Aplicando a lei de Ampère, deduza uma empressão para o módulo do campo magnético na região . Como se comparam os resultados dos itens (b) e (d) para ?
Ver solução completaQuestão 8
Um fio retilíneo de raio conduz uma corrente constante . Um outro fio retilíneo de mesmo raio também conduz uma corrente constante , porém com sentido contrário ao da corrente que flui no primeiro fio. Estime o módulo do campo magnético para pontos externos aos dois fios, isto é, para distâncias (ao centro de um dos fios) maiores que . Suponha que os dois fio possuam uma fina camada de isolante e que eles estejam em contato lateral.
Ver solução completaQuestão 9
Um cabo coaxial é composto por um fio sólido, cilíndrico, circular, de raio , e uma casca espessa, cilíndrica, também circular, coaxial, de raios e , tais que . Ambos os cilindros são muito longos. Através do fio interno, passa uma corrente elétrica, estacionária, cuja densidade de corrente é , enquanto que, através da casca externa, passa uma corrente elétrica, também estacionária, com densidade de corrente .
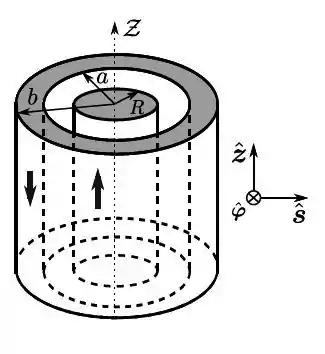
- Qual é a (intensidade de) corrente elétrica no fio interno?
- Qual é a (intensidade de) corrente elétrica na casca externa?
- Determine o campo magnético em cada uma das quatro regiões típicas em que o cabo “divide” o espaço.
Questão 10
Seja uma superfície esférica S, dividida em duas metades e por um grande círculo . A partir da lei de Ampère, podemos afirmar que:
O fluxo do campo magnético através de é proporcional à circulação de corrente através de .
A circulação do campo magnético ao longo de é proporcional à intensidade de corrente através de .
A circulação do campo magnético ao longo de é proporcional à intensidade de corrente através de .
O fluxo do campo magnético através de é proporcional à circulação de corrente através de .
A circulação do campo magnético ao longo de é nula.
Ver solução completaQuestão 11
Um fio condutor retilíneo tem seção transversal circular de raio , como mostrado na figura abaixo. Uma corrente estacionária de intensidade atravessa o fio com sentido para fora do plano do papel, uniformemente distribuída sobre a seção transversal. Desenha-se então uma curva fechada e orientada na forma de um quadrado inscrito no perímetro dessa seção, com a orientação indicada. Nessa situação, podemos afirmar que a circulação do campo magnético produzido pelo fio ao longo de , dada por , vale:
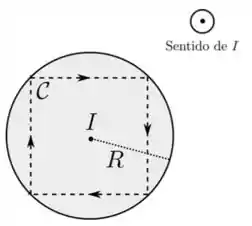
Questão 12
Considere as seguintes três distribuições estacionárias de corrente: (I) Corrente ao longo de um anel circular; (II) Corrente ao longo das geratrizes (ou seja, na direção do eixo) de uma superfície cilíndrica circular muito longa (“infinita”), e (III) solenoide muito longo (“infinito”). Em qual dessas situações é conveniente usar a Lei de Ampère para determinar o campo magnético resultante?
- Somente a I
- Somente a II
- Somente a III
- I e II
- I e III
- II e III
Questão 13
Parte I
Em uma determinada região existe uma densidade de corrente uniforme de no sentido positivo do eixo .
Qual é o valor de quando a integral de linha é tomada ao longo do contorno amperiano formado pelos três segmentos de linha reta que conectam, consecutivamente, os ponto , , e , onde ?
Parte II
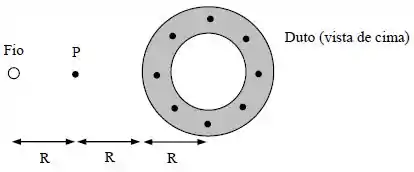
Um duto cilíndrico muito longo, com um raio externo , conduz uma corrente (uniformemente distribuída) (no sentido saindo da página, veja a figura abaixo). Um fio corre paralelo ao duto a uma distância de centro a centro.
Calcule a intensidade (em termo de ), a direção e o sentido da corrente que deve passar no fio para que o campo magnético em seja nulo.
Questão 14
Considere o cabo coaxial muito longo da figura abaixo, formado por um cilindro central de raio e uma casca cilíndrica externa de raios e , concêntrica com cilindro.
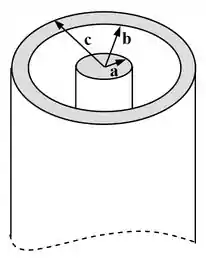
Sabendo que uma corrente flui no cilindro e uma corrente flui na casca cilíndrica (em sentidos opostos):
Calcule o campo magnético (módulo, direção e sentido) em todas as regiões do espaço considerando que as corrente estão uniformemente distribuídas nas seções transversais do cilindro e da casca cilíndrica.
Faça um gráfico do módulo de em função do raio (distância ao centro do cabo).
Ver solução completaQuestão 15
Um fio extremamente longo é dobrado na forma mostrada na figura, de forma a evitar o contato no ponto de cruzamento . O raio da parte circular é e a corrente tem o sentido indicado.
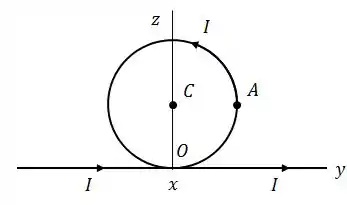
Determine a contribuição da parte linear do fio para o vetor campo magnético no centro e no ponto do círculo.
Determine a contribuição da parte circular do fio para o vetor campo magnético no centro do círculo e o vetor campo magnético total no mesmo ponto.
Em seguida, a parte circular do fio é girada de , sem distorção, em torno do eixo , tornando-se perpendicular à parte linear, de tal forma que a nova posição do ponto tem coordenada positiva.
Determine uma expressão para o vetor campo magnético total no centro do círculo.
Ver solução completaQuestão 16
Um fio cilíndrico de raio transporta uma corrente uniformemente distribuída por sua seção reta e com sentido saindo do papel.
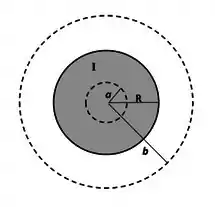
Encontre os raios das espiras amperianas circulares centradas no eixo do fio para as quais o campo magnético gerado pelo fio é dado por:
Ver solução completaQuestão 17
A figura abaixo representa a seção transversal de uma casca cilíndrica muito longa, com raio interno e raio externo . No interior desta casca cilíndrica, existe uma corrente axial . A derivada da corrente elétrica com respeito ao raio é dada pela função .
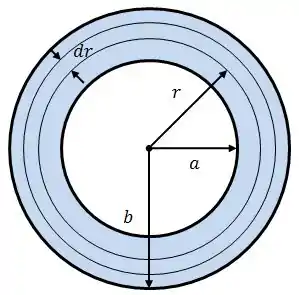
Calcule a intensidade do campo magnético em função do raio quando .
Calcule a expressão da corrente elétrica em função de .
Calcule a expressão da intensidade do campo magnético em função do raio quando .
Ver solução completaQuestão 18
- Determine o vetor campo magnético a uma distância de um fio retilíneo longo percorrido por uma corrente elétrica estacionária de intensidade .
- Determine o vetor campo magnético no centro de uma espira circular de raio percorrida por uma corrente elétrica estacionária de intensidade .
- A figura mostra um fio retilíneo longo, paralelo ao eixo que é percorrido por uma corrente elétrica estacionária e apresenta uma dobra circular de raio , pertencente ao plano . Sabendo que o fio é recoberto por um esmalte isolante, utilize os resultados obtidos nos itens anteriores para determinar o campo magnético resultante no centro da dobra circular.
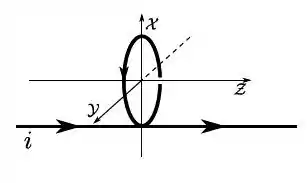
Questão 19
Considere três situações independentes, envolvendo correntes estacionárias de intensidade com módulo e as correspondentes curvas ampèrianas . Qual é a circulação em cada uma das situações?
- , ,
- , ,
- , ,
- , ,
- , ,
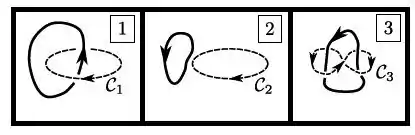
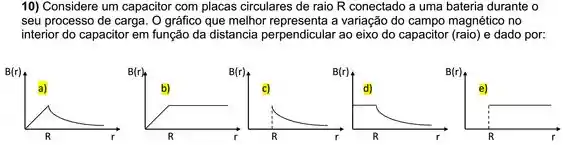
Questão 20
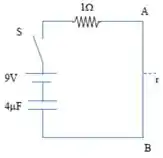
Um capacitor de placas paralelas e circulares está inicialmente descarregado. A partir de um certo instante, ele começa a ser carregado por uma corrente não estacionária. Durante tal processo de carga, considere as seguintes afirmativas: (I) o campo elétrico entre as placas é diferente de zero; (II) o campo magnético entre as placas é zero, e (III) o campo magnético fora das placas é diferente de zero. Indique a alternativa que registra qual(is) dessas afirmações é(são) correta(s).
- I
- II
- III
- I e II
- I e III
- II e III
- I, II e III
- Nenhuma
Questão 21
Um cabo coaxial é composto por um fio sólido, cilíndrico, circular, de raio , envolto por uma casca espessa, cilíndrica, também circular, coaxial, de raios e , tais que . Ambos os cilindros são muito longos e tem o eixo comum . Através do fio interno, passa uma corrente elétrica estacionária, cuja densidade de corrente é dada por , onde e é a distância até o eixo do fio. Através da casca externa, passa uma corrente estacionária, cuja densidade de corrente é dada por , onde .
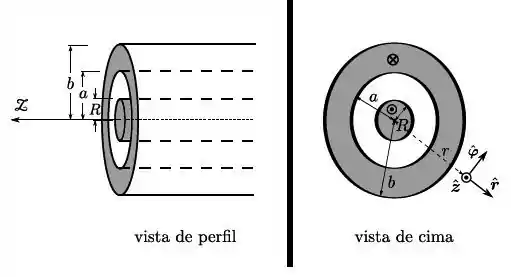
- Qual é a (intensidade de) corrente elétrica no fio interno?
- Qual é a (intensidade de) corrente elétrica na casca externa?
- Determine o campo magnético em cada uma das quatro regiões em que o cabo “divide” o espaço.
Questão 22
- Considere um fio condutor retilíneo, muito longo, percorrido por uma corrente elétrica estacionária de intensidade . Utilizando a Lei de Ampère e que o campo magnético provocado por tal fio retilíneo é puramente circular (ou azimutal), deduza, detalhadamente, uma expressão para tal campo, indicando, com clareza, qual a curva Amperiana utilizada (Sugestão: use coordenadas cilíndricas)
- Utilizando a Lei de Biot-Savart, deduza, detalhadamente, o campo magnético , no centro de um anel condutor circular, de raio , percorrido por uma corrente elétrica estacionária de intensidade .
- Referindo-se agora à figura abaixo, temos um arame com uma parte retilínea muito longa e outra parte circular, de raio e centro . Utilizando os resultados dos itens anteriores, qual deve ser a posição (ordenada) da parte retilínea do arame, de modo que o campo magnético resultante no ponto seja nulo?
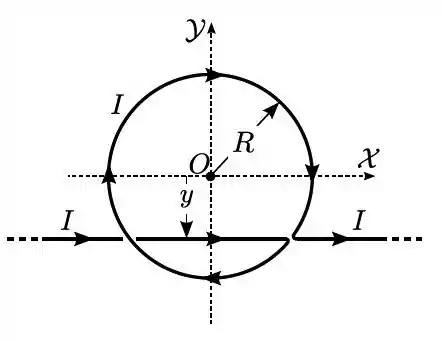
Questão 23
Considere dois fios retilíneos, longos, paralelos, separados por uma distância , pelos quais passam correntes estacionárias e no mesmo sentido. É correto afirmar que o campo magnético resultante será nulo em uma reta coplanar com os fios paralelos aos mesmo que esteja localizada:
- A uma distância de cada um dos fios.
- A uma distância do fio com corrente e do fio com corrente
- A uma distância do fio com corrente e do fio com corrente
- A uma distância do fio com corrente e do fio com corrente
- O campo magnético resultante devido aos dois fios não será nulo em ponto algum.
Questão 24
Durante o processo de carga de um capacitor de placas paralelas por uma corrente , como se comportam os campos elétrico, , e magnético, , entre as placas do capacitor? [estacionário = não depende do tempo]
e não estacionário; e estacionário
e estacionário;
e estacionário; e estacionário
; e estacionário
e não estacionário; e não estacionário
Ver solução completaQuestão 25
Considere um plano infinito com uma densidade superficial de corrente .
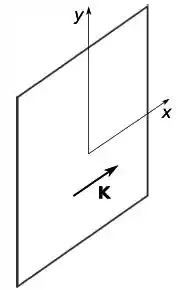
Sabendo que esse plano contém os eixos e (que são perpendiculares entre si) e é perpendicular ao eixo , qual das afirmativas abaixo é verdadeira?
(Obs.: simetria plana é a simetria de translação nas direções e , e simetria axial é a simetria de rotações em torno de um eixo dado)
Pela simetria plana, o campo magnético sempre aponta na direção .
Pela simetria axial em torno de , o módulo do campo magnético independe das coordenadas e .
Pela simetria axial em torno de , o campo magnético sempre aponta na direção .
Pela simetria plana, o módulo do campo magnético independe das coordenadas e .
Pela simetria axial em torno de , o campo magnético sempre aponta na direção .
Ver solução completaQuestão 26
Dois fios retilíneos muito longos, paralelos, a uma distância de entre si, transportam, cada um, uma corrente elétrica estacionária de . O módulo da força magnética por unidade de comprimento que cada um exerce sobre o outro é:
.
.
.
.
.
Ver solução completaQuestão 27
A figura abaixo mostra um fio , que consiste de dois segmentos retilíneos, semi-infinitos, ligados a um outro, semicircular, de raio , transportando uma corrente .
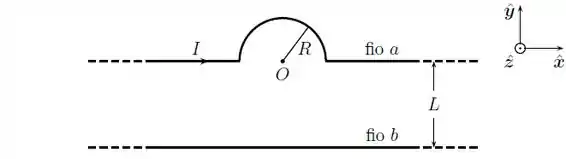
Calcule o vetor campo magnético, gerado pelo fio , no ponto , centro do semicírculo. Justifique cuidadosamente.
Sabendo que um outro fio retilíneo infinito, , está situado a uma distância do fio , paralelo a esse, quais devem ser o valor e o sentido da corrente no fio para que o campo magnético resultante seja nulo em ?
Ver solução completaQuestão 28
Dois condutores retos, longos e paralelos, estão separados por uma distância e são percorridos por correntes elétricas de intensidades e , com os sentidos indicados na figura a seguir. Sendo o comprimento dos condutores igual a , determine a intensidade da força magnética entre eles e diga se ela é atrativa ou repulsiva.
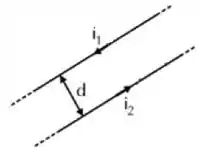
(a) , atrativa.
(b) , repulsiva.
(c) , repulsiva.
(d) , repulsiva.
(e) , atrativa.
Ver solução completaQuestão 29
A figura abaixo mostra uma seção reta de um condutor cilíndrico oco de raios e que conduz uma corrente , cujo vetor densidade de corrente é uniforme.
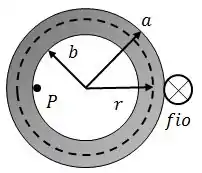
- Obtenha o módulo do campo magnético para , e para ;
- Qual será o módulo de , no ponto , situado em , quando um fio com uma corrente for colocado tangencialmente ao longo do condutor cilíndrico, a uma distância do centro deste?
Questão 31
Um resistor cilíndrico de raio é feito de um material de condutividade e permissividade dielétrica igual ao do vácuo. Uma voltagem variável é aplicada de tal modo que a corrente através do resistor é dada por no sentido do eixo , conforme a figura.
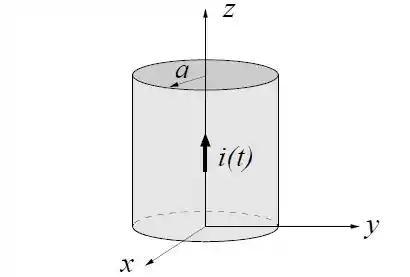
Determine o vetor densidade de corrente elétrica devido às cargas, supondo que seja uniforme no interior do resistor.
Determine o vetor campo elétrico usando a lei de Ohm.
Determine o vetor densidade de corrente de deslocamento .
Use a lei de Ampère- Maxwell para determinar o vetor campo magnético no interior do resistor a uma distância do seu eixo.
Ver solução completaQuestão 32
Um capacitor é construído com duas placas circulares de raio , colocadas a uma distância de uma da outra. Este capacitor é inicialmente carregado. Num determinado instante, passa por ele uma corrente de no sentido mostrado pela figura.
- Indique, numa figura desenhada na folha resposta, o sentido do campo elétrico no interior do capacitor e o sentido da corrente de deslocamento.
- Calcule o campo magnético gerado a uma distância de do eixo de simetria do capacitor na região entre as placas.
- Calcule o campo magnético gerado a uma distância de do eixo de simetria do capacitor na região entre as placas.
Justifique todas as suas respostas.
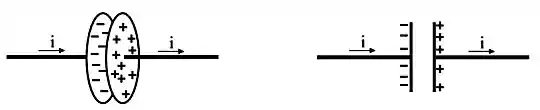
Questão 35
Dois fios longos e paralelos, ambos no plano da página, transportam correntes iguais no mesmo sentido, como mostrado. Qual das seguintes afirmações descreve corretamente a força que age sobre os fios e o campo magnético resultante em pontos ao longo da reta pontilhada, situada a meio caminho entre os fios?
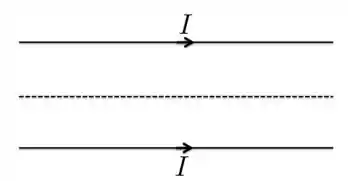
Força Campo
- Repulsiva Nulo;
- Atrativa Não nulo;
- Repulsiva Não nulo;
- Atrativa Nulo;
- Nula Nulo;
Questão 36
A figura abaixo mostra uma curva fechada, orientada, e um trecho de um fio retilíneo, longo, pelo qual passa uma corrente estacionária de intensidade , no sentido indicado. Podemos afirmar que:
Questão 37
A densidade de corrente elétrica que passa num condutor é definida com o a corrente elétrica por unidade de área da seção transversal do condutor. Considere um cabo condutor cilíndrico oco muito longo de raio interno e raio externo , disposto ao longo do eixo , que transporta uma corrente no sentido (para fora do papel). A densidade de corrente na seção transversal é , onde é uma constante e é a distância radial do centro do condutor.
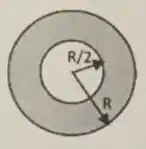
Utilizando a lei de Ampère:
- Determine o valor (módulo) do campo magnético no interior do cabo condutor, numa distância do centro.
- Determine o valor (módulo) do campo magnético no exterior do cabo condutor, para .
- Trace o gráfico do módulo do campo magnético em função da distância ao centro do cabo condutor. Indique no gráfico o valor máximo do campo magnético e o valor de para o qual isso acontece.
- Usando a lei de Ampère, determine o módulo do campo magnético total numa distância .
Considere agora que no centro do cabo (região oca) seja inserido um fio condutor de raio desprezível concêntrico ao cabo, que transporta uma corrente com sentido oposto ao da corrente anterior .
Questão 38
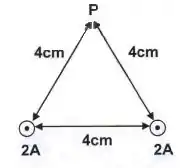
Dois fios retos longos perpendiculares ao plano do papel estão nos vértices de um triângulo equilátero, como mostra a figura. Cada um deles conduz uma corrente de para fora do papel. O campo magnético no terceiro vértice em uma magnitude (em Tesla):
(a)
(b)
(c)
(d)
(e)
Questão 39
. Considere as afirmativas abaixo:
A lei de Ampère-Maxwell, que inclui a corrente de deslocamento, é válida apenas para distribuições de corrente estacionárias.
Correntes não circundadas por uma curva fechada e orientada não contribuem para a circulação de campo magnético ao longo de , mas contribuem para o campo magnético em pontos sobre .
Devido à não-observação de monopolos magnéticos, o fluxo de campo magnético através de uma superfície fechada deve ser sempre nulo.
São VERDADEIRAS as afirmativas:
Escolha uma opção:
e
Nenhuma delas
e
e
e
Ver solução completa
Questão 40
A figura abaixo mostra a seção reta de um condutor cilíndrico concêntrico oco, infinitamente longo, de raio externo e raio interno , carregando uma corrente total . Supondo que a densidade de corrente seja homogênea por todo condutor. A intensidade do campo magnético fora do condutor , dentro do condutor e fora do condutor valem respectivamente:
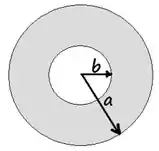
a)
b)
c)
d)
e)
Ver solução completa
Questão 42
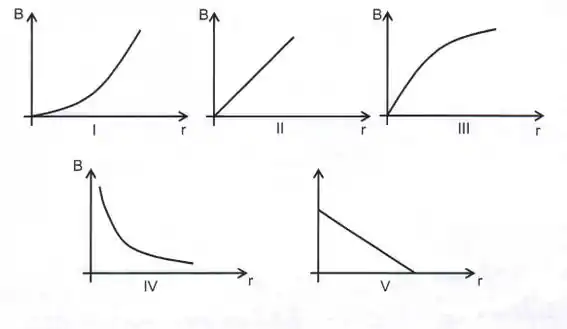
Qual gráfico abaixo mostra corretamente a magnitude do campo magnético gerado por um fio linear, fino e infinitamente longo em função da distância perpendicular ao fio, que conduz uma corrente elétrica?
(a) III
(b) I
(c) V
(d) IV
(e) II
Questão 44
O cabo coaxial mostrado na figura consiste de um cilindro condutor longo e sólido de raio envolto por um condutor cilíndrico oco de raio . Os dois conduzem correntes de iguais intensidades , mas de sentidos opostos.
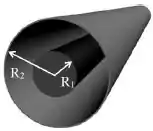
A densidade de corrente é uniforme nos dois condutores. A intensidade do vetor campo magnético nas seguintes regiões , , respectivamente são iguais a:
Ver solução completa
Questão 46
Considere uma espira retangular de lados e () e um fio retilíneo infinito, coplanar. Sabendo-se que o fio retilíneo é paralelo aos lados longos da espira e que o fio e a espira portam, respectivamente, correntes para a direita e e no sentido horário, assinale a única opção incorreta.
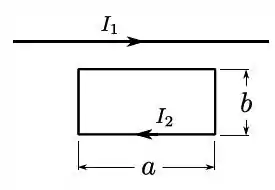
- A soma das forças nos lados curtos da espira é nula;
- A força em cada um dos lados curtos da espira é nula;
- A soma das forças nos lados longos da espira é não nula;
- As forças sobre os lados longos da espira estão na mesma direção;
- A força total sobre a espira é perpendicular ao fio retilíneo.
Questão 47
Um cilindro condutor muito comprido, com o seu eixo orientado ao longo do eixo , transporta uma corrente elétrica cuja densidade é . A densidade de corrente, definida como a corrente por unidade de área, é simétrica em relação ao eixo do cilindro, mas não é uniforme e varia radialmente de acordo com a seguinte relação:
Onde “” é o raio do cilindro, “” é a distância radial entre o ponto considerado e o eixo do cilindro e “” é uma constante com unidades [].
a) Calcule o valor da corrente total que passa através da seção reta do fio.
b) Utilizando a Lei de Ampère, calcule o módulo do campo magnético na região.
c) Obtenha a expressão para a corrente contida em uma seção reta circular de raio , centralizada no eixo do cilindro.
d) Utilizando a Lei de Ampère, calcule o módulo do campo magnético na região .
e) Como se comparam os resultados dos itens b) e d) quando ?
Ver solução completaQuestão 48
Um cilindro condutor infinito, de seção transversal circular de raio , possui uma densidade de corrente estacionária, mas não-uniforme dada por , onde é uma constante positiva, é a distância até o eixo do cilindro e é o vetor unitário da direção paralela ao eixo do cilindro. Nessa situação, podemos afirmar que o campo magnético produzido pelo cilindro em pontos dentro e fora dele tem intensidade proporcional a, respectivamente
a) e
b) e
c) e
d) e
e) e
f) e
Ver solução completaQuestão 49
. Em uma região cilíndrica de raio , há um campo elétrico homogêneo dado por , onde e são duas constantes e é o tempo.
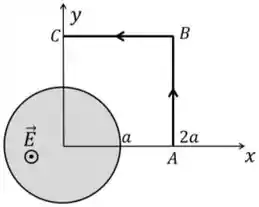
A integral de linha do campo magnético , ao longo do caminho aberto , onde , e é:
. Nenhuma das alternativas
. A integral de linha é zero, pois não á corrente
Ver solução completaQuestão 50
Em um condutor cilíndrico muito longo, maciço, de raio passa uma corrente cuja densidade varia quadraticamente com a distância ao eixo do cilindro: , onde é uma constante.
Calcule a corrente através do disco de raio mostrado na figura.
Calcule o vetor para .
Calcule o vetor para .
Expresse em função da corrente total e .
Ver solução completaQuestão 51
Sobre a corrente de deslocamento presente na lei de Ampère-Maxwell, podemos afirmar que:
(a) Não há diferença conceitual entre a corrente de deslocamento e a corrente elétrica.
(b) É apenas um artifício matemático para que a lei de Ampère seja consistente.
(c) Está associada a transporte de cargas entre as placas de um capacitor.
(d) A corrente de deslocamento e a corrente elétrica são conceitualmente diferentes, mas numericamente iguais.
(e) Não há interpretação física para a corrente de deslocamento.
Ver solução completaQuestão 52
Em um modelo clássico para o átomo de hidrogênio, um elétron se desloca em movimento circular uniforme com velocidade escalar e raio em torno de um próton fixado na origem. Supondo que a corrente associada ao movimento do elétron pode ser tratada como uma corrente estacionária, qual é a intensidade do campo magnético produzido por ela na posição do próton?
Questão 53
A lei de Ampère-Maxwell é válida
quando existe um alto grau de simetria na geometria da situação.
quando não há simetria.
quando existe corrente de deslocamento.
quando o campo magnético é constante.
em todas as situações anteriores.
Ver solução completaQuestão 54
Considere dois fios retilíneos, longos, paralelos, separados por uma distância , pelos quais passam correntes estacionárias e , no mesmo sentido. É correto afirmar que o campo magnético resultante será nulo...
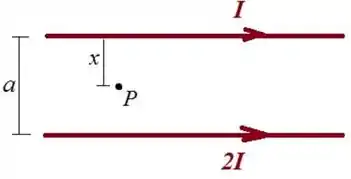
(a) a uma distância de cada um dos fios
(b) a uma distância do fio com corrente e do fio com corrente .
(c) a uma distância do fio com corrente e do fio com corrente
(d) a uma distância do fio com corrente e do fio com corrente
(e) a nenhuma distância pois o campo magnético resultante devido aos dois fios não será nulo em ponto algum.
Ver solução completaQuestão 55
Determine, respectivamente, a circulação do campo magnético para cada uma das curvas orientadas da figura abaixo, , e .
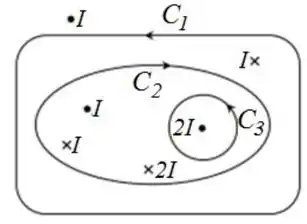
(a) , ,
(b) , ,
(c) , ,
(d) , ,
(e) , ,
Ver solução completaQuestão 56
A figura abaixo mostra a seção transversal de um cilindro condutor longo de raio , percorrido por uma corrente de densidade uniforme de módulo e apontando para dentro da página. Nele existe uma cavidade também cilíndrica de raio , centrada com o eixo do cilindro. Considerando-se que o eixo do cilindro é o eixo z, calcule o módulo do vetor campo magnético em um ponto P que está a uma distância do centro do cilindro.
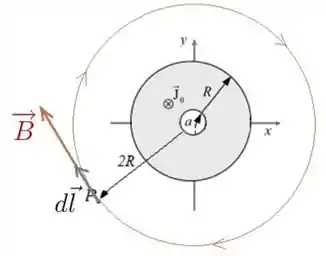
(a)
(a)
(a)
(a)
(a)
Ver solução completaQuestão 57
Um cilindro circular maciço, infinito e condutor, de raio , possui uma densidade de corrente estacionária, , onde é uma constante positiva, é a distância ao eixo do cilindro e é um vetor unitário cuja direção é paralela ao eixo do cilindro. Assinale a alternativa cujo gráfico melhor representa o comportamento do módulo do campo magnético produzido pelo cilindro como função da distância .
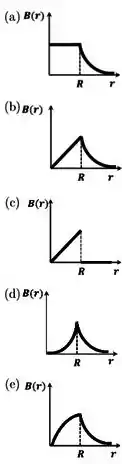
Questão 58
Dois fios longos retilíneos entram em uma sala através de uma porta. Um dos fios transporta uma corrente de para dentro da sala e o outro transporta uma corrente de para fora dela. O módulo da integral de linha ao longo do contorno da sala é aproximadamente
Questão 59
Considere a espira quadrada de lado da figura abaixo, percorrida por uma corrente de intensidade constante no sentido horário. O sistema de coordenadas está indicado na figura, com o semieixo positivo-z saindo do plano do papel em direção ao leitor. Lembre-se que .
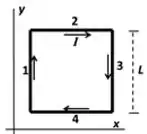
- Em toda a região da espira existe um campo magnético externo homogêneo dado por . Qual (ou quais) dos segmentos de fio, numerados na figura, não sofrem força magnética devida ao campo externo? Justifique.
- Calcule, em relação ao centro da espira, o vetor torque resultante devido ao campo externo nas condições do item (a)
- Desconsidere agora o campo externo e suponha que os fios e tenham comprimento de apenas . Deste modo, os fios e podem ser considerados “muito longos”, paralelos e separados pela distância de . A corrente na espira continua com intensidade . Encontre o módulo da força que o fio 1 exerce numa seção de 2,0 cm do fio 3 afastada de suas extremidades e responda se essa força é de atração ou repulsão.
- Sabendo que , encontre o valor da nova corrente que percorre a espira quadrada e informe também o seu sentido (horário ou anti-horário)
Considere agora a próxima figura, em que a linha amperiana aparece envolvendo os fios e da espira quadrada analisada anteriormente.
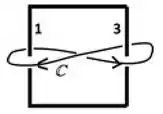
Questão 60
Determine a circulação para as três curvas fechadas orientadas respectivamente.
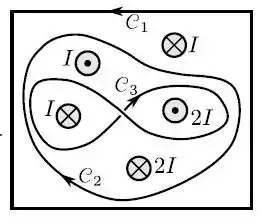
- pois todas são perpendiculares.
Questão 61
Um cabo coaxial é composto por um fio sólido, cilíndrico, circular, de raio , e uma casca espessa, cilíndrica, também circular, coaxial, de raios e , tais que . Ambos os cilindros são muito longos. Através do fio interno, passa uma corrente elétrica, estacionária, cuja densidade de corrente é , enquanto que, através da casca externa, passa uma corrente elétrica, também estacionária, com densidade de corrente .
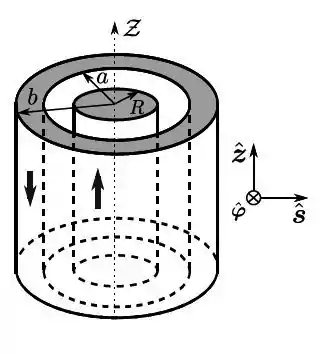
- Qual é a (intensidade de) corrente elétrica no fio interno?
- Qual é a (intensidade de) corrente elétrica na casca externa?
- Determine o campo magnético em cada uma das quatro regiões típicas em que o cabo “divide” o espaço.
Questão 62
A figura a seguir mostra a seção reta de três fios que conduzem correntes estacionárias, com intensidade de mesmo módulo , que atravessam o plano da figura com sentidos indicados na mesma.
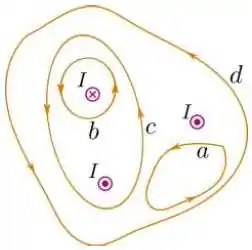
Quatro curvas orientadas indicadas pelas letras até são apresentadas na figura. A alternativa a seguir que melhor relaciona a circulação do campo magnético em cada curva é
.
.
.
.
.
Ver solução completaQuestão 63
Seja uma superfície esférica S, dividida em duas metades e por um grande círculo . A partir da lei de Ampère, podemos afirmar que:
O fluxo do campo magnético através de é proporcional à circulação de corrente através de .
A circulação do campo magnético ao longo de é proporcional à intensidade de corrente através de .
A circulação do campo magnético ao longo de é proporcional à intensidade de corrente através de .
O fluxo do campo magnético através de é proporcional à circulação de corrente através de .
A circulação do campo magnético ao longo de é nula.
Ver solução completaQuestão 64
Seja um fio retilíneo infinito, paralelo ao eixo , por onde flui uma corrente estacionária . Adjacente a esse fio e a uma distância dele, existe uma espira retangular no plano de lados e , conforme mostra a figura.
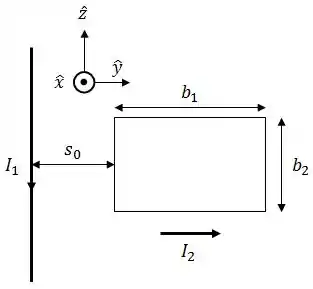
Sabendo-se que a espira carrega uma corrente e que o campo gerado pelo fio é dado (vide formulário), determine:
A força que o fio retilíneo exerce sobre o lado horizontal superior da espira.
A força que o fio retilíneo exerce sobre o lado vertical esquerdo da espira.
A força total sobre a espira (Justifique).
Ver solução completaQuestão 65
A figura abaixo ilustra um condutor cilíndrico maciço infinito, de raio , que é percorrido por uma dada corrente elétrica constante . Sabe-se que, neste condutor, a densidade de corrente varia com a distância ao eixo do cilindro de acordo com a relação , onde é uma constante positiva e denota a distância ao eixo de simetria do cilindro. A permeabilidade magnética do vácuo é denotada por . Atenção: quando possível, expresse seus resultados em termos de , , e .
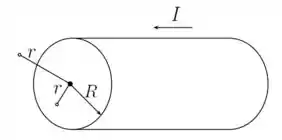
(a) Calcule o módulo do campo magnético no interior do cilindro ().
(b) Calcule o módulo do campo magnético no exterior do cilindro ().
(c) Esboce um gráfico mostrando como o campo magnético varia com a distância ().
Ver solução completaQuestão 66
Por um fio muito longo com de diâmetro passa uma corrente . Esta corrente provoca um campo magnético de a uma distância de medida em relação ao centro do fio. Calcule o módulo da densidade uniforme de corrente que passa por este fio.
(a) .
(b)
(c) 4
(d)
(e)
Ver solução completaQuestão 67
Um cilindro condutor, muito longo, oco, de paredes finas (como um tubo) de raio carrega uma corrente uniformemente distribuída ao longo do seu comprimento. Qual dos gráficos abaixo descreve mais precisamente a magnitude do campo magnético produzido por esta corrente como uma função da distância ao centro do cilindro?
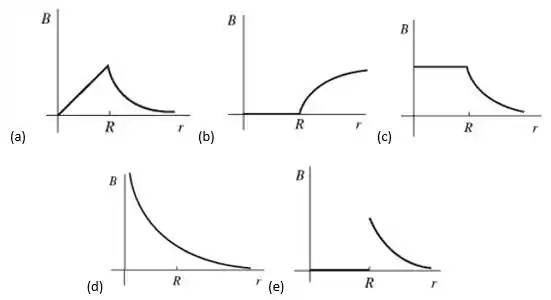
Questão 68
(II) A figura abaixo mostra a seção reta de uma casca cilíndrica muito longa de raio interno e raio externo , coaxial com o eixo . Pela casca flui, na direção positiva do eixo (direção saindo do papel), uma corrente uniformemente distribuída através de sua seção reta.
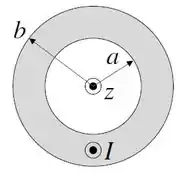
(a) (0,5 ponto) Calcule o vetor densidade de corrente na região , onde é a distância ao eixo da casca cilíndrica.
(b) (1,0 ponto) Calcule o vetor campo magnético na região .
Ver solução completaQuestão 69
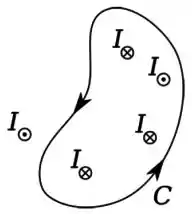
A figura abaixo mostra uma região atravessada perpendicularmente por várias correntes estacionárias com intensidades de mesmo módulo . Por convenção, as correntes que saem da página são representadas por ⊙ e as que entram na página por ⊗.
Estão representados, também, três diferentes caminhos fechados, orientados, para a determinação da integral .
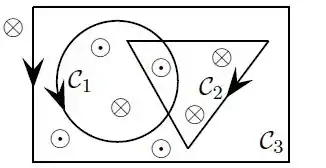
Assinale a opção abaixo que melhor indica a relação entre tais integrais para os diferentes caminhos.
e
e
Não podemos determinar sem conhecermos as dimensões dos caminhos utilizados
Ver solução completaQuestão 70
Considere um fio de comprimento por onde passa uma corrente colocado ao longo do eixo , conforme a figura.
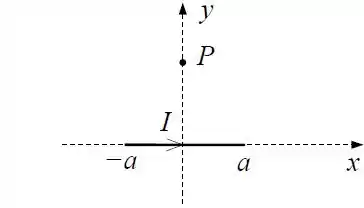
Usando a lei de Ampère, calcule o campo magnético em para o fio infinito do item .
Ver solução completaQuestão 71
A figura mostra a seção transversal de uma casca cilíndrica muito longa de raio interno e raio externo , que conduz uma corrente uniformemente distribuída. O fio mostrado à direita só será usado no item .
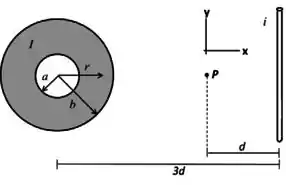
Utilizando a Lei de Ampère, calcule o módulo do vetor magnético a uma distância do centro para .
Conforme mostra a figura, a casca cilíndrica está paralela ao eixo e um fio retilíneo muito longo, que transporta uma corrente , está paralelo ao eixo . O campo magnético resultante destes dois objetos é medido fora da casca cilíndrica no ponto , e vale: . Sabendo que , encontre as intensidades das correntes (na casca) e (no fio) e seus respectivos sentidos (forneça as respostas em termos dos vetores unitários)
Sugestão: o módulo do vetor campo magnético de uma distribuição cilíndrica muito longa, que transporta uma corrente , à distância , vale:
Ver solução completaQuestão 72
a) Um condutor reto infinito conduzindo uma corrente é dividido em duas partes semicirculares idênticas de raio . Cada parte semicircular conduz a corrente , conforme mostra a Figura 1. Calcule o vetor campo magnético no centro da espira circular assim formada.
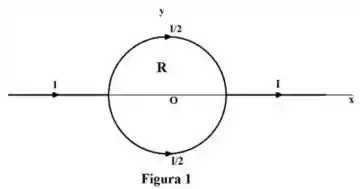
b) Um condutor reto infinito conduzido uma corrente é dobrado conforme mostra a Figura 2. Os fios paralelos semi-infinitos são muito próximos, de modo que suas correntes (opostas) se cancelam mutuamente. Calcule o vetor campo magnético no centro da espira circular assim formada.
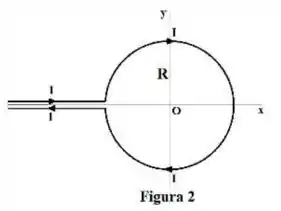
c) Calcule o vetor campo magnético devido aos fios semi-infinitos da Figura 1 (que conduzem a corrente ) em um ponto arbitrário do eixo vertical (perpendiculares ao papel) que contém o centro da espira circular. Sugestão: os dois fios semi-infinitos que conduzem a corrente são equivalentes a um fio infinito que conduz a corrente e um fio finito que conduz a corrente .
Ver solução completaQuestão 73
Considere um fio retilíneo muito longo de raio e centrado ao longo do eixo no qual passa uma corrente estacionária (ao longo da direção ), conforme mostra a figura abaixo. A corrente elétrica é distribuída de forma que sua densidade de corrente é dada por: (se ), e caso contrário, sendo uma constante.
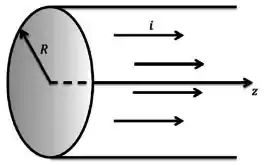
- Determine a corrente total em função de e .
- Usando a lei de Ampère, encontre o vetor campo magnético na região .
- Usando a lei de Ampère, encontre o vetor magnético na região .
Questão 74
A figura abaixo mostra três fios condutores finos, retilíneos e infinitos transportando correntes estacionárias com as intensidades e sentidos indicados. Considere as quatro curvas fechadas , , e indicadas na figura. Seja o módulo da circulação do campo magnético resultante ao longo da curva (). Nesta situação, podemos afirmar que:
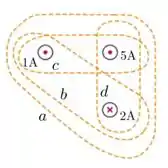
Questão 75
Um cabo coaxial consiste em um cilindro condutor maciço, infinito, de raio coaxial a uma casca condutora cilíndrica, também infinita, de raio e espessura desprezível. Uma seção transversal deste cabo é mostrada na figura abaixo. O cilindro transporta uma corrente estacionária de intensidade , uniformemente distribuída sobre sua seção transversal e com sentido para fora do plano da folha, enquanto a casca transporta uma corrente estacionária de mesma intensidade no sentido inverso.
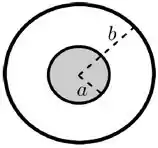
Determine o campo magnético produzido pelo cabo (módulo, direção e sentido) em um ponto a uma distância do eixo. Considere todas as regiões distintas do espaço, dadas por (i) , (ii) e (iii) . Justifique cuidadosamente todo o desenvolvimento.
Ver solução completaQuestão 76
Infinitos fios com diâmetro desprezível e de comprimento infinito repousam no plano . Cada fio transporta uma corrente, cujo vetor aponta na direção . Considere que a densidade linear de fios é (número de fios por unidade de comprimento). Calcule o vetor campo magnético produzido por este arranjo de fios.
Ver solução completaQuestão 77
Um cilindro condutor, maciço, de raio possui densidade de corrente estacionária e não uniforme dada por , onde é uma constante positiva, é a distância ao eixo do cilindro e é o unitário da direção correspondente a esse eixo.
- Determine a corrente total que atravessa uma seção transversal do cilindro.
- Determine o campo magnético (módulo, direção e sentido) produzido pelo cilindro em todo o espaço. Justifique cuidadosamente todos os argumentos utilizados.
Questão 78
Considere as seguintes afirmações:
- O campo magnético de uma espira circular por onde passa uma corrente estacionária satisfaz a lei de Ampère.
- A afirmação é verdadeira devido à simetria axial da espira.
- Se a espira fosse quadrada, a lei de Ampère não seria válida.
- Se a espira fosse quadrada, a lei de Ampère seria válida, desde que se escolhessem curvas amperiana que passassem pelo centro do quadrado.
São verdadeiras as afirmativas:
Somente
e
, e
e
Somente
Ver solução completaQuestão 79
Considere um fio cilíndrico circular, sólido, de raio e com altura infinita, como mostrado na figura abaixo. Através de tal fio, há uma densidade de corrente elétrica estacionária, mas não uniforme dada por , onde é uma constante positiva, é a distância até o eixo do fio e o seu correspondente unitário.
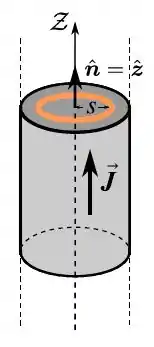
(a) Determine a intensidade de corrente elétrica que passa através de uma seção transversal qualquer do fio. Sugestão: tome como elemento de superfície um anel de raio e espessura infinitesimal .
(b) Sendo um ponto arbitrário com coordenadas cilíndricas , informe qual(is) componente(s) do vetor campo magnético é (são) nula(s), indicando ainda de que coordenada(s) ela(s), de fato, pode(m) depender. Justifique.
(c) Com base no resultado do item (b), identifique uma curva fechada e orientada apropriada para a dedução do campo magnético, e determine uma expressão para a circulação de tal campo ao longo dela:
(d) Aplicando a lei de Ampère, deduza expressões para o vetor campo magnético (i) fora
e (ii) dentro do fio.
(e) Faça um esboço cuidadoso do gráfico do módulo de como funções de , marcando explicitamente
quaisquer pontos relevantes.
Ver solução completaQuestão 80
Considere as seguintes três afirmativas sobre a lei de Ampère: (I) ela só vale quando há um alto grau de simetria da distribuição de correntes; (II) ela só vale quando as correntes forem estacionárias, e (III) ela só vale quando os campos magnéticos forem estacionários. Assinale a alternativa que indica qual(is) de tais afirmações são corretas.
- Nenhuma
- Apenas a I
- Apenas a II
- Apenas a III
- Apenas a I e a II
- Apenas a I e a III
- Apenas a II e a III
- Todas
Questão 81
A figura abaixo mostra uma seção transversal de dois fios condutores longos, idênticos, com comprimento , estendidos paralelamente um ao lado do outro ao longo da direção . Por estes fios circulam correntes e , em sentidos opostos, sendo no mesmo sentido do eixo , conforme a figura.
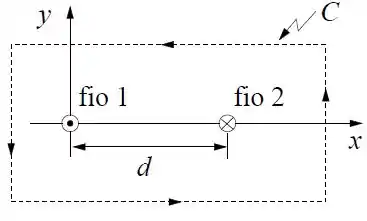
Usando a lei de Ampère, calcule o vetor campo magnético de um fio infinito onde passa uma corrente .
Calcule a força de interação por unidade de comprimento que o fio 1 exerce sobre o fio 2. A força é atrativa ou repulsiva?
Calcule a integral sobre o percurso orientado no sentido anti-horário, conforme a figura.
Ver solução completaQuestão 82
Um tubo de cobre muito longo de raio interno e raio externo é percorrido por uma corrente uniformemente distribuída “saindo” da página (sentido positivo do eixo ).
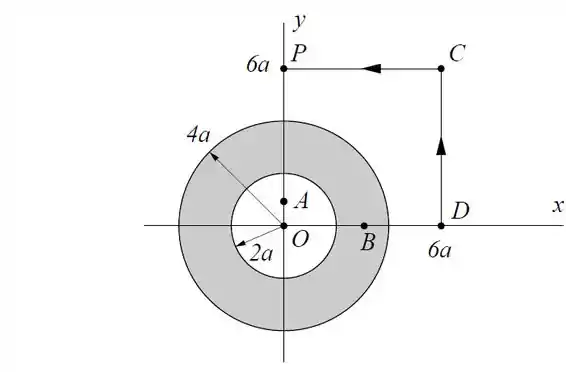
- Determine o vetor campo magnético em coordenadas cartesianas (isto é, na forma ) nos pontos , e .
- Determine a integral de linha do campo magnético ao longo do caminho fechado , onde e , no sentido indicado.
- Determine a integral de linha do campo magnético ao longo do trecho , no sentido indicado.
Questão 83
(Capítulo 29.4 – Exercício 44) A figura 29-67 mostra duas curvas fechadas que envolvem duas espiras que ocnduzem correntes e . Determine o valor da integral (a) para a curva 1 e (b) para a curva 2.
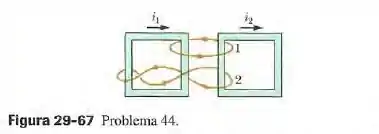
Questão 84
(Capítulo 29.4 – Exercício 47) A densidade de corrente no interior de um fio cilíndrico longo de raio é paralela ao eixo central e o módulo varia linearmente com a distância radial de acordo com a equação , em que . Determine o módulo do campo magnético (a) para ; (b) para ; (c) para .
Ver solução completaQuestão 85
Um fio retilíneo muito longo, alinhado com o eixo x e transportando uma corrente, é colocado num campo magnético externo uniforme de módulo , como representado na figura abaixo
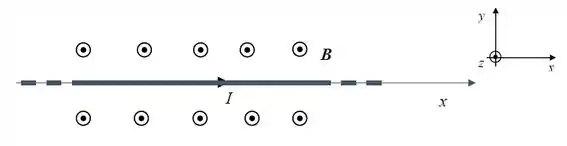Utilizando o sistema de referência indicado, determine os pontos no espaço onde o
campo magnético resultante é nulo.
Ver solução completaQuestão 86
. Um cilindro condutor infinito, circular, possui uma densidade de corrente estacionária, mas não-uniforme, dada por , onde é uma função exclusiva da distância ao eixo do cilindro e é o unitário da direção paralela a este eixo. Considerando o sistema usual de coordenadas cilíndricas, sobre o campo magnético produzido pelo cilindro, é correto afirmar que:
Escolha uma opção:
A única componente não-nula do campo é a componente radial e esta componente depende apenas da distância .
A única componente não-nula do campo é a componente radial e esta componente depende apenas da coordenada ao longo do eixo.
A única componente não-nula do campo é a componente circunferencial e esta componente depende apenas da coordenada ao longo do eixo.
A única componente não-nula do campo é a componente radial e esta componente depende apenas do ângulo polar .
A única componente não-nula do campo é a componente circunferencial e esta componente depende apenas do ângulo polar .
A única componente não-nula do campo é a componente circunferencial e esta componente depende apenas da distância .
Não é possível afirmar nada sobre o campo magnético sem conhecer os detalhes da função .
Ver solução completaQuestão 87
. Um certo meio condutor possui três tipos de portadores de cargas , e . O número desses portadores por unidade de volume vale , e , respectivamente, e eles se deslocam com velocidades , e , respectivamente. Sabendo que o meio se encontra globalmente neutro, de forma que não há cargas em excesso em nenhum ponto dele, quais são os valores de e da densidade de corrente total neste meio?
Escolha uma opção:
e
e
e
e
e
e
e
e
Ver solução completaQuestão 88
Considere quatro condutores cilíndricos, cujas seções retas circulares possuem centros nos vértices de um quadrado, como mostrado na figura abaixo.
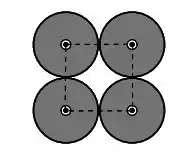
A curva que corresponde a esse quadrado é chamada de . A corrente (uniforme e estacionária) em cada um desses condutores é , e tem o sentido mostrado na figura. Um quinto condutor é colocado na região central limitada pelos quatro condutores, e é percorrido por uma corrente estacionária . Qual deve ser o valor da corrente nesse quinto condutor para que a integral seja igual a zero?
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 89
Um capacitor de placas planas paralelas, circulares e cujo raio das placas é muito maior que a distância entre as mesmas está inicialmente descarregado. A partir de um certo instante, o capacitor começa a ser carregado por uma corrente que cresce linearmente com o tempo , onde . Sobre os campos elétrico e magnético que podem eventualmente surgir entre as placas durante o carregamento do capacitor, pode-se afirmar que:
- Surgirá apenas um campo elétrico estacionário
- Surgirão um campo elétrico estacionário e um campo magnético não estacionário, colineares entre si
- Surgirá apenas um campo elétrico não estacionário.
- Surgirão um campo elétrico não estacionário e um campo magnético estacionário, colineares entre si
- Surgirão um campo elétrico não estacionário e um campo magnético estacionário, perpendiculares entre si
- Surgirão um campo elétrico e um campo magnético, ambos não estacionários, e perpendiculares entre si
Questão 90
Na figura vemos quatro amperianas circulares concêntricas com um fio cuja corrente é dirigida para fora do papel.
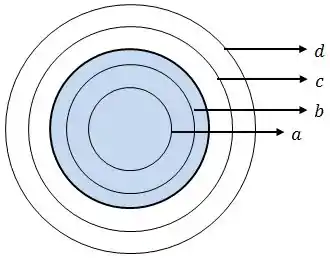
A corrente é uniforme em toda a seção reta do fio (região azulada). Colocando as amperianas na ordem decrescente do valor absoluto de ao longo da curva, obtemos:
;
e empatados, , ;
, , ;
é impossível ordenar sem saber o valor da corrente;
e empatados, , ;
Ver solução completaQuestão 91
Em uma casca cilíndrica de comprimento infinito, raio e coaxial com o eixo passa uma corrente , uniformemente distribuída, que flui no sentido de negativo. No interior desta casca cilíndrica existe uma região cilíndrica (região cinza na figura) também de comprimento infinito, raio e coaxial com o eixo onde há um campo elétrico uniforme , onde é uma constante positiva e é o tempo.
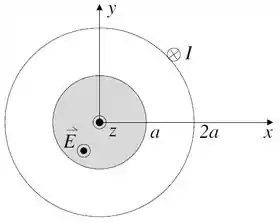
(a) (1,5 ponto) Desconsiderando a casca cilíndrica por onde passa corrente, calcule o vetor campo magnético em todo o espaço (regiões e , onde é a distância ao eixo ).
(b) (1,0 ponto) Determine o vetor campo magnético devido somente à corrente que passa pela casca cilíndrica em todo o espaço.
(c) (1,0 ponto) Calcule o valor da corrente para que o campo magnético seja nulo para .
Ver solução completaQuestão 92
Um contorno amperiano planar engloba dois fios retilíneos por onde fluem as correntes e . Todos os sentidos estão indicados na figura a seguir. O fio corta perpendicularmente o plano que contém o contorno , mas o fio o faz segundo o ângulo ().
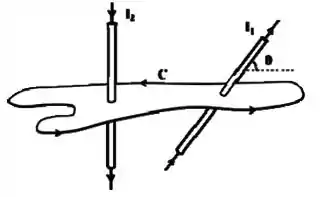
Sabendo que e que a integral ao longo de fornece o valor , encontre o valor da intensidade de corrente .
Ver solução completa
Questão 94
Um fio A de comprimento muito grande é percorrido por uma corrente no sentido positivo do eixo-z, como mostra a figura. Esse fio está envolto por uma casca cilíndrica , também de comprimento, de raio interno e raio externo . A corrente que percorre a casca cilíndrica não é homogênea, obedecendo a uma densidade de corrente ,onde é a distância com relação ao centro do cilindro.
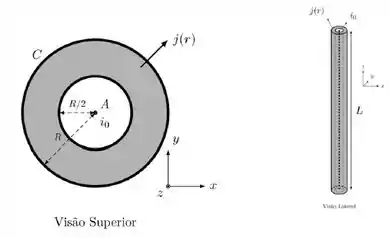
a) Considere que a densidade de corrente do fio é onde é desconhecido.
Encontre o valor de j0 para que o campo magnético possua um valor constante na região interior da casca cilíndrica e encontre a magnitude desse campo (não se esqueça de considerar também a influência do campo do fio no interior). Encontre também qual a direção da corrente (z positivo ou z negativo).
b) Considere que a densidade de corrente é no eixo-z positivo (diferente do item (a). Se aplicamos na região do espaço um campo magnético constante na direção positiva do eixo x, calcule o vetor força magnética resultante na casca cilíndrica C devido ao campo magnético aplicado. Sugestão: considere que a casca é na realidade composta por diversos fios finos de corrente infinitesimal .
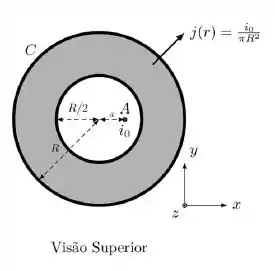
c) Considere que a densidade de corrente é agora constante e que o fio A foi deslocado de a com relação ao centro, como mostra a nova figura. Encontre a força magnética que o a casca C realiza no fio A. Justifique sua resposta com cálculos.
Questão 95
Considere as seguintes quatro distribuições de corrente:
(I) Fio condutor fino, retilíneo e infinito, transportando uma corrente não-estacionária;
(II) Espira plana, circular, transportando uma corrente estacionária;
(III) Cilindro condutor sólido, infinito, de seção transversal circular, transportando uma corrente estacionária uniformemente distribuída sobre sua seção transversal.
Assinale a opção que indica corretamente para qual(is) dessa(s) distribuição(ões) a lei de Ampere é válida para uma curva fechada e orientada arbitrária.
a) Apenas na distribuição I.
b) Apenas na distribuição II.
c) Apenas nas distribuições II e III.
d) Apenas nas distribuições I e III.
e) Apenas nas distribuições I e II.
Ver solução completaQuestão 96
Uma placa condutora infinita de espessura é posicionada de forma que seu plano médio coincide com o plano de um sistema de coordenadas, como mostrado na figura abaixo. Ela possui uma densidade de corrente constante dada por . Nessa situação, o campo magnético produzido pela placa nas regiões e vale, respectivamente:
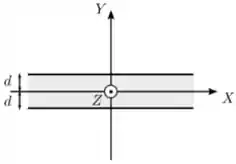
Escolha uma:
e
e
e
e
e
e
e
e
Ver solução completaQuestão 97
Uma espira condutora circular de raio transporta uma corrente estacionária de intensidade com sentido indicado na figura abaixo. Traça-se, então, uma curva amperiana circular , de raio , perpendicular ao plano da espira, com centro em um ponto da mesma e com a orientação indicada. Sobre essa situação, é CORRETO afirmar que:
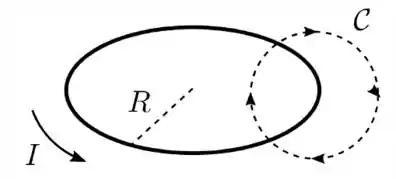
- Pela lei de Ampère, o campo magnético produzido pela espira tem o mesmo módulo em todos os pontos de .
- Por simetria, o campo magnético produzido pela espira é tangente a em todos os pontos desta curva.
- Pela lei de Ampère, o campo magnético produzido pela espira é tangente a em todos os pontos desta curva.
- Por simetria, o campo magnético produzido pela espira tem o mesmo módulo em todos os pontos de .
- A circulação do campo magnético produzido pela espira ao longo de vale .
Questão 98
. A densidade de corrente no interior de um fio cilíndrico muito longo e retilíneo de raio é paralela ao eixo do cilindro. Seu módulo varia linearmente com a distância radial de acordo com a equação , onde é uma constante.
Calcule o campo magnético para .
Calcule o campo magnético para .
Ver solução completaQuestão 99
. . O módulo do campo elétrico entre as duas placas paralelas circulares e de raio do capacitor da figura abaixo é dado por , com em volt por metro segundo e em segundo. Calcule a corrente de deslocamento em todas as regiões do espaço. Qual o sentido do campo magnético gerado (horário ou anti-horário) quando se olha a figura no sentido do campo elétrico, i.e., de baixo para cima.
Ver solução completaQuestão 100
Um capacitor usual de placas muito grandes (“infinitas”), planas e paralelas, está sendo lentamente carregado. Em termos dos vetores unitários , e , assinale a opção que melhor indica a direção e sentido dos campos elétrico e magnético, respectivamente, dentro do capacitor.
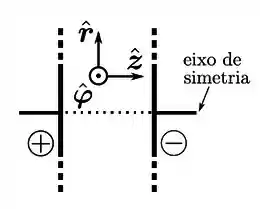
- e
- e
- e
- e
- e
- e
Questão 101
Um fio espesso é constituído por um cilindro condutor infinito de seção transversal circular de raio . Nesse cilindro, passa uma densidade de corrente uniforme e estacionária dada por , onde é o unitário da direção paralela ao eixo do cilindro. Nessa situação, o que se pode dizer a respeito do campo magnético produzido por esse fio?
- O campo magnético é nulo em qualquer ponto sobre o eixo do fio
- O campo magnético é paralelo ao eixo do fio em qualquer ponto no interior do mesmo
- O campo magnético é uniforme no interior no fio
- O campo magnético é perpendicular ao eixo do fio e aponta radialmente para fora em qualquer ponto no exterior do mesmo
- O módulo do campo magnético cai com o inverso do quadrado da distância ao eixo do fio no exterior do mesmo
Questão 102
(Capítulo 29 – Problemas Adicionais – Exercício 87c) A figura 29-87 mostra uma seção reta de um cabo coaxial longo de raios e . Corrente de mesmo valor e sentidos opostos estão uniformemente distribuídas nos dois condutores. Escreva expressões para o módulo do campo magnético em função da distância radial (c) para .
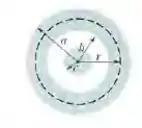
Questão 103
(Capítulo 29.4 – Exercício 43) A figura 29-66 mostra uma seção reta de um fio cilíndrico longo de raio que conduz uma corrente uniforme de . Determine o móulo do campo magnético produzido pela corrente a uma distância do eixo do fio igual a (a) ; (b) ; (c) (superfície do fio) e (d) .
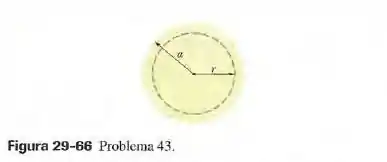
Questão 104
(Capítulo 29 – Problemas Adicionais – Exercício 79c) Um condutor longo, oco, cilíndrico (raio interno , raio externo ) é percorrido por uma corrente de . A distribuição uniformemente na seção reta. Um fio longo e fino coaxial com o cilindro conduz uma corrente de no sentido oposto. Determine o módulo do campo magnetico (c) a de distância do eixo central do fio e do cilindro.
Ver solução completaQuestão 105
(Capítulo 29.4 – Exercício 46) Oito fios são perpendiculares ao plano do papel nos pontos indicados na Figura 29-69. O fio conduz uma corrente , em que. Para os fios com ímpar, a corrente é para fora do papel; para os fios com par, a corrente é para dentro do papel. Determine o valor de ao longo da curva fechada mostrada na figura, no sentido indicado.
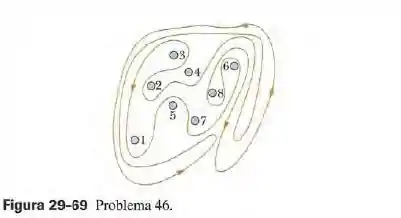
Questão 106
Uma região cilíndrica de de raio possui um campo elétrico paralelo ao eixo da região. O campo elétrico é uniforme na região, mas está aumentando a uma taxa de .
A intensidade do campo magnético a uma distância de do eixo é:
Ver solução completa
Questão 107
Uma fita metálica de largura conduz uma corrente . Portanto, a densidade superficial de corrente é
- Encontre a expressão da intensidade do campo magnético em pontos próximos à superfície da fita. Considerando que a largura da fita é , e a corrente vale , qual o valor do campo magnético.
Questão 108
Um fio condutor fino, retilíneo e infinito carrega uma corrente estacionária de intensidade , como mostrado na figura abaixo. Considere uma curva imaginária fechada e orientada na forma de um círculo de raio , desenhada de forma que seu plano seja perpendicular ao eixo do fio, mas seu centro não coincida com ele, como indicado.
Questão 109
A Figura abaixo mostra quatro correntes iguais a e cinco linhas amperianas envolvendo estas correntes.
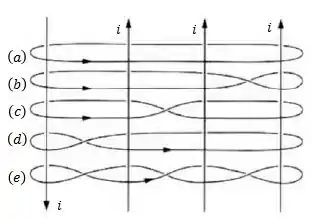
Calcule o valor da integral ao longo das curvas amperianas nas direções dadas.
Define-se densidade superficial de corrente elétrica a grandeza: , onde é a corrente e é a área da superfície considerada.
Considere agora um fio muito longo de seção circular e de raio onde passa uma densidade de corrente com direção paralela ao eixo central. O módulo desta densidade de corrente varia linearmente com o raio do fio de acordo com a equação , onde é uma constante. Determine, usando a lei de Ampere o campo magnético em .
Ver solução completaQuestão 110
ii. Usando a lei de Ampére calcule o vetor campo magnético no interior de um condutor cilíndrico infinito de raio por onde passa uma corrente uniformemente distribuída através de sua seção reta.
Ver solução completaQuestão 111
Considere um fio fino, retilíneo e infinito, transportando uma corrente estacionária de intensidade . Traça-se, então, uma curva amperiana circular, raio , que circunde o fio num plano perpendicular a ele, mas de forma que o fio não passe pelo centro da amperiana, como mostrado na figura abaixo. Nessa situação, qual das afirmativas abaixo é VERDADEIRA?
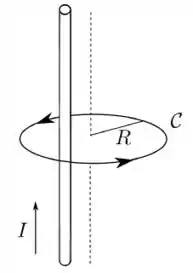
- Pela lei de Ampère, a circulação do campo magnético produzido pelo fio tem módulo igual a .
- Por simetria, o campo magnético produzido pelo fio é sempre tangente à amperiana.
- Por simetria, o módulo do campo magnético produzido pelo fio tem o mesmo valor em todos os pontos da amperiana.
- Pela lei de Ampère, o campo magnético produzido pelo fio é sempre tangente à amperiana.
- Pela lei de Ampère, o módulo do campo magnético produzido pelo fio tem o mesmo valor em todos os pontos da amperiana.
Questão 112
A figura mostra a seção transversal de um cilindro condutor longo de raio , percorrido por uma corrente de densidade uniforme de módulo apontando para dentro da página. Nele existe uma cavidade oca também cilíndrica, de raio 𝑎 = 4 𝑐𝑚, centrada com o eixo do cilindro. Sabendo que o cilindro se encontra sobre o eixo , calcule o módulo do vetor campo magnético em um ponto que está a uma distância do centro do cilindro.
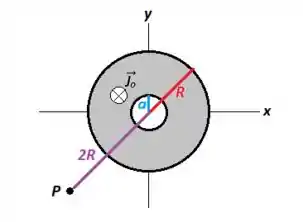
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 113
Caso 1
O gráfico mostra o comportamento do módulo do campo magnético criado por um fio retilíneo cilíndrico muito longo como função da distância radial até seu eixo de simetria. Para , é linear. Para , a função é inversamente proporcional a .
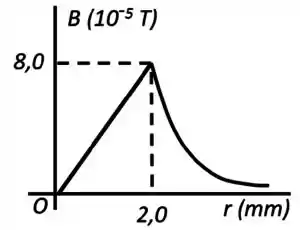
- A densidade de corrente é uniforme dentro do fio? Justifique a sua resposta cuidadosamente usando a lei de Ampère.
- Suponha, agora, que a corrente no fio sentido e que a densidade de corrente seja uniforme. Calcule o vetor , em .
- Em função de e , calcule a razão de modo que a força magnética resultante do fio sobre a espira seja nula.
Caso 2
Considere, agora, uma espira em forma de trapézio (figura abaixo), que tem dois lados paralelos entre si e também paralelos a um fio muito longo pelo qual passa uma corrente .
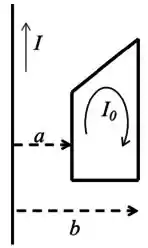
Pela espira circula uma corrente no sentido horário, mas seus lados não paralelos estão blindados do campo magnético causado pelo fio. O segmento da espira mais próximo ao fio e está à distância do fio, e o segmento mais distante mede e está à distância do fio.
Questão 114
Um fio condutor cilíndrico muito longo e de seção reta de raio está envolto por uma casca cilíndrica condutora fina de raio , formando um cabo coaxial cujo eixo coincide com o eixo . Pelo fio passa uma corrente , na direção positiva do eixo , uniformemente distribuída através de sua seção reta. Na casca cilíndrica passa uma corrente total , na direção negativa do eixo , conforme a figura.
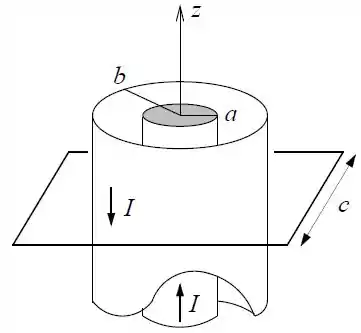
Calcule o vetor campo magnético nos pontos onde ( é a distância do ponto até o eixo ).
Calcule o vetor campo magnético na região .
Calcule a integral ao longo do quadrado de lado coaxial com o eixo , conforme a figura.
Ver solução completaQuestão 115
Um cabo coaxial é formado por um cilindro circular reto, condutor, maciço, de raio e uma casca cilíndrica condutora de raio , coaxial ao cilindro. Uma corrente estacionária de intensidade flui ao longo do eixo do cilindro, uniformemente distribuída sobre sua seção transversal, e uma corrente estacionária de mesma intensidade flui ao longo da casca cilíndrica, em sentido oposto à do cilindro.
Calcule o fluxo de campo magnético através de uma superfície retangular com dois lados paralelos à direção radial, se estendendo por toda a região do item anterior, e dois lados paralelos ao eixo do cabo, de comprimento .
Ver solução completaQuestão 116
Um cabo coaxial é formado por um cilindro circular reto, condutor, maciço, de raio e uma casca cilíndrica condutora de raio , coaxial ao cilindro. Uma corrente estacionária de intensidade flui ao longo do eixo do cilindro, uniformemente distribuída sobre sua seção transversal, e uma corrente estacionária de mesma intensidade flui ao longo da casca cilíndrica, em sentido oposto à do cilindro.
A partir do resultado acima, determine a auto-indutância por unidade de comprimento deste cabo.
Ver solução completaQuestão 117
Considere um solenóide toroidal de raio médio , com seção transversal de área e voltas de fio enroladas de forma compacta ao longo de seu comprimento.
Utilizando a lei de Ampère, determine a intensidade do campo magnético a uma distância da origem (eixo do toróide). Assuma que as linhas de campo no interior do solenóide são circulares (e de fato são, mesmo nessa situação arbitrária).
Ver solução completaQuestão 118
Um cabo coaxial é formado por um cilindro circular reto, condutor, maciço, de raio e uma casca cilíndrica condutora de raio , coaxial ao cilindro. Uma corrente estacionária de intensidade flui ao longo do eixo do cilindro, uniformemente distribuída sobre sua seção transversal, e uma corrente estacionária de mesma intensidade flui ao longo da casca cilíndrica, em sentido oposto à do cilindro.
Utilizando a lei de Ampère, determine a intensidade do campo magnético no interior da região entre o cilindro e a casca, ou seja, para , onde é a distância ao eixo do cilindro.
Ver solução completaQuestão 119
Considere uma espira retangular de lados e () e um fio retilíneo infinito, coplanar a espira. Sabendo-se que o fio retilíneo é paralelo aos lados longos da espira e que o fio e a espira portam, respectivamente, correntes para direita e no sentido horário, assinale a opção incorreta
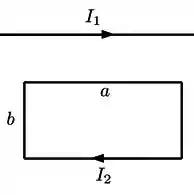
(a) A soma das forças nos lados de comprimento da espira é nula
(b) A força em cada um dos lados de comprimento da espira é nula
(c) A soma das forças nos lados de comprimento da espira é não nula
(d) As forças sobre os lados de comprimento da espira estão na mesma direção e tem sentidos contrários
(e) A força total sobre a espira é perpendicular ao fio retilíneo
Ver solução completaQuestão 120
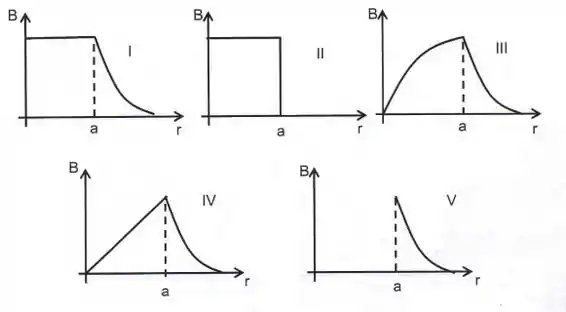
Um condutor cilíndrico maciço de raio conduz uma corrente uniformemente distribuída, paralela ao eixo de simetria, sobre a sua secção transversal do cilindro. Qual dos gráficos abaixo mostra corretamente a intensidade do campo magnético como função da distância a partir do centro do cilindro?
(a) II
(b) I
(c) V
(d) IV
(e) III
Questão 121
Um fio condutor muito longo e de seção cilíndrica de raio está envolto por uma casca
cilíndrica de raio , formando um cabo coaxial. No fio há uma densidade de corrente
uniforme e na casca uma densidade de corrente superficial , sendo
e constantes positivas. Expresse suas respostas em termos dos parâmetros
dados:
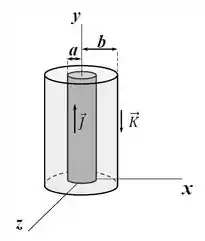
- Calcule o campo magnético nos pontos onde ( é a distância do ponto até o eixo ).
- Calcule o campo magnético na região exterior da casca cilíndrica ().
- Determine o valor de tal que o campo seja nulo na região .
Questão 122
Considere um capacitor ideal, constituído por duas placas circulares, paralelas, muito grandes, muito próximas e que apresentam distribuições uniformes de cargas. Este capacitor está em processo de carregamento e portanto as cargas acumuladas nas placas são função do tempo: temos numa das placas e na outra. Qual é a opção que melhor descreve o que ocorre entre as placas desse capacitor?
(a) Cria-se um campo elétrico e um campo magnético, ambos não estacionários.
(b) Cria-se um campo elétrico uniforme e não estacionário, e um campo magnético nulo.
(c) Cria-se um campo elétrico uniforme e estacionário, e um campo magnético nulo.
(d) cria-se um campo elétrico e um campo magnético, ambos uniformes e estacionários.
(e) Cria-se um campo magnético uniforme e estacionário, e um campo elétrico nulo.
Ver solução completaQuestão 123
4 – Uma casca condutora cilíndrica muito longa de raio interno e raio externo transporta a corrente distribuída uniformemente por toda a área de sua seção transversal, entre e (ver a figura abaixo). Derive uma expressão para a magnitude do campo magnético devido a esta corrente, como uma função da distância radial do eixo central, para cada uma das seguintes regiões:
a)
Questão 124
4 – Uma casca condutora cilíndrica muito longa de raio interno e raio externo transporta a corrente distribuída uniformemente por toda a área de sua seção transversal, entre e (ver a figura abaixo). Derive uma expressão para a magnitude do campo magnético devido a esta corrente, como uma função da distância radial do eixo central, para cada uma das seguintes regiões:
c)
Questão 125
Um fio de cobre, cuja resistividade elétrica é e constante dielétrica praticamente igual a 1, tem área de seção reta uniforme igual a .
Num dado instante, a corrente que passa pelo fio é de , mas está crescendo à taxa de . O número que melhor se aproxima da razão entre a corrente de deslocamento dentro do fio e a corrente de condução, nesse instante, é
Ver solução completa
Questão 126
Em uma região cilíndrica, há um campo elétrico que varia com o tempo e paralelo ao eixo desta região. Se é a distância ao eixo da região, a intensidade do campo magnético dentro desta região é:
proporcional a
proporcional a
proporcional a
proporcional a
Ver solução completaQuestão 127
Um fio condutor na figura abaixo conduz uma corrente no sentido indicado. Para e os trechos são retilíneos e estão ao longo de e , respectivamente (fios semi- infinitos). Para e menores do que , o condutor forma um quarto de círculo com raio , conforme a figura 1.
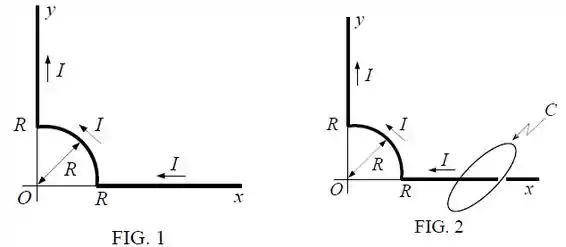
Quais são os campos no ponto devido aos segmentos retilíneos do fio?
Qual é o campo no ponto devido ao segmento circular?
Determine o valor da integral de linha do vetor ao longo do percurso circular fechado não coplanar com os fios e centrado no eixo , conforme a figura 2.
Ver solução completaQuestão 128
Três cilindros condutores, circulares, retos, infinitos e idênticos são posicionados de forma que seus eixos são paralelos e cada um toca os outros dois. Suas seções transversais são mostradas na figura abaixo. Cada um dos cilindros é atravessado por uma corrente estacionária de mesma intensidade , uniformemente distribuída sobre suas seções transversais, fluindo para fora do plano do papel. Considere a curva fechada mostrada na figura, formada por um triângulo cujos vértices coincidem com os eixos dos cilindros nesta seção. A circulação do campo magnétio através de , definida por , é dada por:
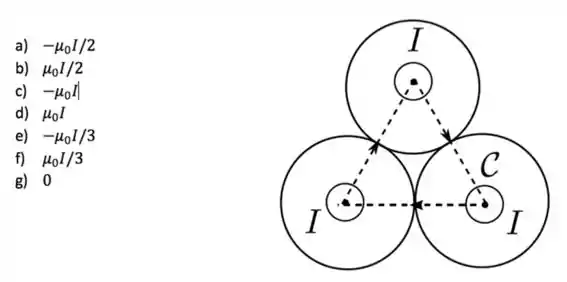
Questão 129
A figura abaixo mostra três espiras condutoras circulares transportando correntes estacionárias com intensidades e sentidos indicados. Qual é o valor da circulação do campo magnético resultante produzido pelas três espiras ao longo da curva fechada e orientada mostrada na figura, ?
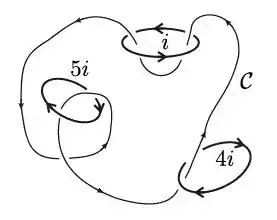
Questão 130
Considere um fio condutor envolvido por uma camada cilíndrica condutora coaxial ao fio, de raio interno e raio externo (a região logo ao redor do fio, até a distância , é vácuo). O fio é percorrido pr uma corrente , e a camada é percorrida por uma corrente uniformemente distribuída, na mesma direção de , mas com sentido oposto. Considere o fio e a camada como sendo muito longos.
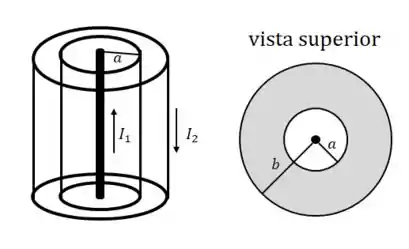
a) Calcule a densidade de corrente na camada cilíndrica.
Calcule o módulo do campo magnético a uma distância do fio (eixo da camada), tal que:
b) .
c) .
d) .
Ver solução completaQuestão 131
Dois fios 1 e 2, infinitos e paralelos, separados pela distância , conduzem no vácuo, cada um, uma corrente , em sentidos opostos, conforme a figura.
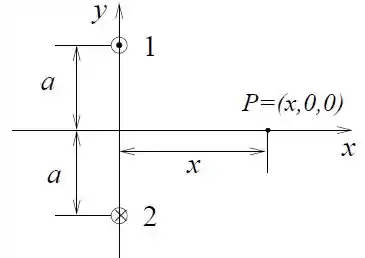
- Usando a lei de Ampère, calcule o vetor campo magnético produzido por um fio infinito por onde passa uma corrente a uma distância do fio.
- Calcule o vetor campo magnético produzido pelos dois fios no ponto .
- Calcule o vetor força por unidade de comprimento exercida no fio 2 pelo fio 1.
Questão 132
A figura abaixo mostra uma seção transversal de dois fios condutores longos (fio 1 e fio 2) estendidos paralelamente um ao outro, ao longo da direção . Por estes fios circulam correntes e , em sentidos opostos, sendo no mesmo sentido do eixo , conforme a figura.
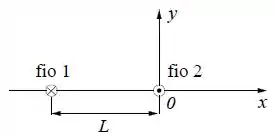
Usando a Lei de Ampère calcule o vetor campo magnético de um fio infinito por onde passa uma corrente .
Calcule o vetor campo magnético total devido aos dois fios mostrados na figura para um ponto qualquer do eixo com .
Ver solução completaQuestão 133
4 – Uma casca condutora cilíndrica muito longa de raio interno e raio externo transporta a corrente distribuída uniformemente por toda a área de sua seção transversal, entre e (ver a figura abaixo). Derive uma expressão para a magnitude do campo magnético devido a esta corrente, como uma função da distância radial do eixo central, para cada uma das seguintes regiões:
b)
Questão 135
Em um condutor cilíndrico muito longo, maciço, de raio passa uma corrente cuja densidade varia linearmente com a distancia ao eixo do cilindro segundo a expressão , onde é uma constante.
Calcule a corrente através do disco de raio mostrado na figura.
Calcule o vetor para .
Calcule o vetor para .
Ver solução completaQuestão 136
Por um condutor cilíndrico maciço e infinito de raio passa uma corrente estacionária e axial uniformemente distribuída através de sua seção reta. O campo magnético a uma distância radial do eixo do condutor, em coordenadas cilíndricas , é igual a
e .
e .
e .
e .
e .
Ver solução completaQuestão 137
Considere o cabo coaxial muito longo da figura ao lado, formado por duas cascas cilíndricas concêntricas com raios internos , e raios externos , , respectivamente. Uma corrente uniforme flui na casca cilíndrica interna com o sentido para fora do plano do papel e uma corrente uniforme com sentido desconhecido flui na casca cilíndrica externa.
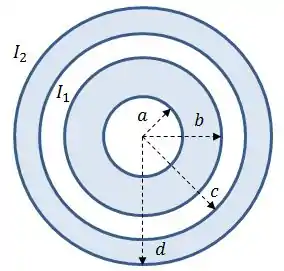
Calcule a intensidade do campo magnético nas regiões:
;
;
;
Sabendo que e que a amplitude do campo magnético em tem o valor de , calcule o valor da corrente em função da corrente , indicando seu sentido.
Calcule a amplitude do campo magnético em em função da corrente .
Ver solução completaQuestão 138
A figura abaixo mostra uma curva fechada, orientada, e um trecho de um fio retilíneo, longo, pelo qual passa uma corrente estacionária de intensidade , no sentido indicado.
Podemos afirmar que:
;
;
;
;
;
Ver solução completaQuestão 139
Suponha que para a espira fechada da figura, o resultado da integral é Quais são a direção e o sentido da corrente no fio?
(a) .
(b)
(c) .
(d) “saindo” da página.
(e) “entrando” na página.
Ver solução completaQuestão 140
Considere correntes elétricas de mesma intensidade, entrando ou saindo da página da prova, conforme os circuitos abaixo.
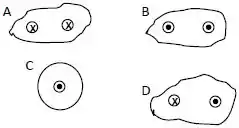
Circuito : Duas correntes entrando
Circuito : Duas correntes saindo
Circuito : Uma corrente saindo
Circuito : Uma corrente entrando e outra saindo
Integrando no sentido anti-horário, classifique a integral de linha do campo magnético, ou seja, , começando do maior positivo.
Ver solução completa
Questão 141
Um circuito condutor é composto por dois fios retilíneos semi-infinitos e uma parte circular, representados pelas linhas escuras, conforme mostrado na figura abaixo. Ele está contido no plano e conduz uma corrente no sentido indicado. Para e os trechos são retilíneos (fios semi-infinitos). Para e , o condutor tem a forme de três quartos de circunferência com raio .
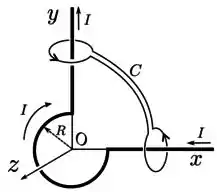
- Calcule o vetor campo magnético na origem devido aos segmentos lineares do fio.
- Calcule o vetor campo magnético na origem do sistema de coordenadas devido à parte circular.
- Determine o valor da integral ao longo do percurso indicado na figura.
Questão 142
Três cilindros condutores, circulares, retos, infinitos e idênticos são posicionados de forma que seus eixos são paralelos e cada um toca os outros dois. Suas seções transversais são mostradas na figura abaixo. Cada um dos cilindros é atravessado por uma corrente estacionária de mesma intensidade , uniformemente distribuída sobre suas seções transversais, fluindo para fora do plano da página. Considere a curva fechada e orientada mostrada na figura, formada por um triângulo cujos vértices coincidem com os eixos dos cilindros nesta seção. A circulação do campo magnético através de , definida por , é dada por
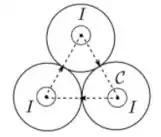
a)
b)
c)
d)
e)
Ver solução completaQuestão 143
Um cilindro condutor infinito, de seção transversal circular de raio , possui uma densidade de corrente estacionária, mas não-uniforme dada por , onde é uma constante positiva, é a distância até o eixo do cilindro e é o vetor unitário da direção paralela ao eixo do cilindro. Nessa situação, podemos afirmar que o campo magnético produzido pelo cilindro em pontos dentro dele tem módulo proporcional a:
Escolha uma:
.
.
.
.
.
.
.
Ver solução completa