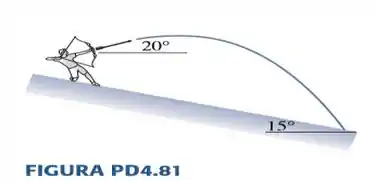
81. Um arqueiro parado em pé sobre uma rampa inclinada para baixo em dispara uma flecha em um ângulo de acima da horizontal, como mostra a FIGURA PD4.81. A que distância sobre a rampa a flecha atingirá a mesma se for disparada a e de de altura em relação ao solo
Passo 1
Tudo bem senhores!? Aqui vamos nós de novo pra mais uma questãozinha de Cinemática!
E pra resolver esse tipo de questão, já sabe né?
Primeiramente, bora fazer um esboço pra ajudar a entender melhor o nosso problema...
De modo que obtemos então, a seguinte imagem abaixo...
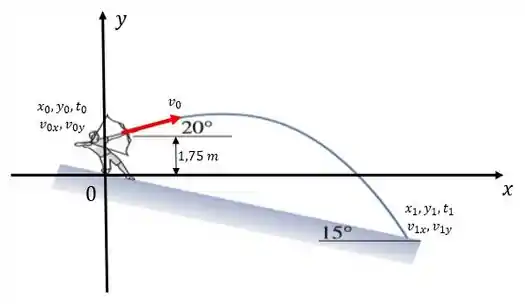
E pelo que sabemos dos problemas de movimento oblíquo e também do que lemos no enunciado, tiramos que...
Onde o objetivo aqui é encontrar a distância sobre a rampa que a flecha atingirá... no caso precisaremos de e .
Depois; por incrível que pareça, basta usar Pitágoras. É isso mesmo que você acabou de ler. Esse teorema vai acompanhar a gente até a eternidade, rs rs rs!
Por isso, mãos à obra!
Passo 2
Bom! Tomando como o instante inicial do movimento da flecha, pra facilitar a nossa resolução, bora dividir o movimento dela em duas partes, vertical e horizontal...
Na horizontal, em , nossa flecha não tem aceleração influenciando seu movimento. Sendo assim, ela executa um movimento uniforme, com velocidade constante.
Olhando pra nossa figura, ficamos então com...
E substituindo os valores numéricos de cada variável;
Obtemos a equação que descreve o movimento em ...
Passo 3
Indo agora pra direção vertical, temos nessa direção a presença da aceleração da gravidade para baixo influenciando a trajetória da flecha.
Desse modo, peguemos a equação abaixo da posição para o movimento uniformemente variado... É claro, usando as variáveis da nossa figura, né!?
Esse é a nossa aceleração da gravidade , com sinal negativo porque aponta para baixo...
O que nos faz ficar com...
Desse modo, substituindo os valores conhecidos...
Obtemos o valor da equação que descreve o movimento vertical!
Tamo indo bem!
Passo 4
Por fim, como sabemos que a flecha atinge o solo formando um ângulo de com a horizontal, no sentido horário, isso significa que a seguinte relação abaixo é valida...
O ângulo fica negativo, por causa que no sentido horário, a convenção adotada é negativa. Isso aí já é manjado, mano!
Desse modo, substituindo as equações de posição obtidas anteriormente...
Temos a seguinte equação para resolver...
Como é uma equação do grau no formato , basta usar a já conhecida fórmula abaixo...
E uma vez que só trabalhamos com tempo positivo, então...
Passo 5
Obtido o tempo total do lançamento da flecha, basta substituir esse tempo nas nossas duas fórmulas de espaço...
Bora lá... Primeiro para ;
E depois para :
Feito isso! Como foi falado anteriormente... Uma vez que o lançamento foi feito em uma rampa triangular... Para descobrir a distância percorrida pela flecha sobre a rampa, basta usar Pitágoras;
E voilà! Terminamos aqui!