Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Randall D. Knight- Ed: 2º - Capítulo 4.Exercícios e Problemas - Ex. 47

Um amigo seu que é jogador de beisebol deseja determinar a velo cidade com que ele consegue arremessar a bola. Ele fica em pé sobre um monte de terra, 4,0   m acima do solo ao redor, e arremessa a bola horizontalmente. A bola aterrissa a 25   m de distância.

a. Qual é o módulo da velocidade de arremesso?

b. Durante o lançamento, você não teve certeza de que o arremesso foi feito exatamente na horizontal. Ao observar atentamente os arremessos, você nota que o ângulo de lançamento parece variar de 5° abaixo da horizontal a 5° acima da mesma. Qual é a faixa de valores de velocidade com que a bola poderia ter sido lançada?

Passo 1

O exercício nos dá

y 0 = 4,0   m

x = 25,0   m

θ = 5 °

E o que ele quer saber

v 0 x = ?

E o esqueminha do movimento é

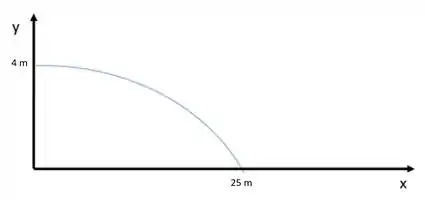
Ouuu seja galerinha, o movimento é uma parábola, do que em relação a x é um Movimento Uniforme e a y é Uniformemente Variado.

Passo 2

  1. Poxa, o exercício pede v 0 x , nas não temos todos os dados para colocar em uma das equações do movimento, então o que podemos descobrir? O tempo! Vejamos a baixo!

    2. y - y 0 + v 0 y t - t 0 + a y t - t 0 2 2 →   0 = 4 + 0 - 9,8   t 2 2 → t = 0,9035   s

    Agora para encontrar v 0 x usaremos a formulazinha

    x = x 0 + v 0 t - t 0 → 25 = 0 + v 0 x 0,9035 → v 0 x = 27,7   m / s

    A velocidade inicial foi de 27,7 m/s rapaziada!

    Passo 3

  2. Foi dito no exercício que o ângulo inicial pode variar ± 5°. O que isso quer dizer? Que a velocidade será afetada diretamente com isso! Então podemos escrever como

v 0 y = ± s e n   θ   v 0

E substituindo o que sabemos na equação do movimento de y

y = y 0 ± v 0   s e n   θ t - t 0 - g t - t 0 2 2 → 0 = 4 ± v 0 s e n   θ - g t 2 2     ( i )

E agora no em x, lembrando que é UM, então a aceleração é zero!

x = x 0 + v 0 y t - t 0 → 25 = 0 + v 0 cos ⁡ θ   t → t = 25 v 0 cos ⁡ θ       ( i i )

Juntando (i) e (ii), ouuu seja, agregando o tempo na equação de y, temos

0 = 4 ± v 0 s e n   θ   25 v 0   cos ⁡ θ - g 2 25 v 0 cos ⁡ θ 2 → v 0 2 = g   625 2 cos 2 ⁡ θ   1 4 ± 25 tan ⁡ θ =

  9,8 × 625 2 cos 2 ⁡ 5 ° 4 ± 25 tan ⁡ 5 ° = 6125 2 × 0,992 ( 4 ± 25 × 0,087 = 6125 7,936 ± 4,315  

Então v 0   assume os valores 22,3   m / s e 44   m / s

Resposta

a.   27,7   m / s

b. 22,3   m / s e 44   m / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que o ângulo inicial α 0 da Figura 3.26 seja 42,0 ° e que d seja igual a 3,0 m. Onde o dardo e o macaco se encontrarão, se a velocidade inicial do dardo for a) 12,0 m/s? b) 8,0 m/s?c) O que oc
Um balão de 124 kg carregando um cesto de 22 kg está descendo a uma velocidade constante de 20,0 m/s. Uma pedra de 1,0 kg é atirada do cesto em uma trajetória perpendicular a dobalão que desce, com ve
Bombeiros estão lançando um jato de água em um prédio em chamas, usando uma mangueira de alta pressão que dispara água a uma velocidade escalar de 25,0m / s . Quando sai da mangueira, a água passa a a
Um canhão, localizado a 60,0m da base de um rochedo vertical, lança uma bomba de 15k g , a 45 ° sobre a horizontal e em direção ao rochedo. a) Qual deve ser a velocidade mínima naboca do canhão para q
Pelé chuta uma bola de futebol com velocidade inicial tal que o componente vertical é igual a 16,0 m/s e o componente horizontal é igual a 20,0 m/s. Despreze a resistência do ar. a) Quanto tempo a bol