Uma bola de é jogada de baixo para cima com velocidade inicial de , da borda de um rochedo que mede de altura. No instante em que a bola é jogada, uma mulher começa a correr da base do rochedo, com velocidade constante de . Ela corre em linha reta no nível do solo, e a resistência do ar sobre a bola é desprezível.

a) A que ângulo sobre a horizontal a bola deve ser jogada para que a corredora consiga pegá-la antes que atinja o solo e que distância ela percorre até conseguir isso?

b) Desenhe a trajetória da bola do ponto de vista de i) uma pessoa em repouso no solo e ii) a corredora.

A equação pro movimento em y é:

Com o y sendo positivo pra cima e o ponto de partida igual a zero, temos:

Daí podemos achar o tempo:

E a equação em x, que é da mulher:

Como ,

Então a distância percorrida pela mulher é:

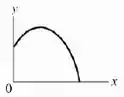
Do ponto de vista de uma pessoa no solo, a trajetória é parabólica, pois ela vê tanto a bola subindo e descendo, quanto se deslocando para o lado. A composição desse movimento é uma parábola com boca para baixo e sua representação gráfica é:

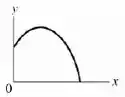
Agora olha só que legal. Do ponto de vista da corredora, a bola não tem movimento horizontal. Ela tem apenas movimento vertical, de subida e descida. Isso significa que para ela a bola só sobe e desce, uma vez que ela está se movendo em conjunto com a bola lateralmente. A representação gráfica vai ser uma linha reta vertical, subindo e descendo na vertical, mas na mesma posição na horizontal. O gráfico é: