Uma bola é arremessada em direção a um penhasco de altura com de rapidez, em um angulo de ° acima da horizontal. Ela aterrissa na borda do penhasco s mais tarde,
a. Qual a altura do penhasco?
b. Qual é a altura máxima atingida pela bola?
c. Qual é o valor da velocidade de impacta com o solo?
Passo 1
Primeiro vamos pegar os dados e fazer um esqueminha para começar o problema
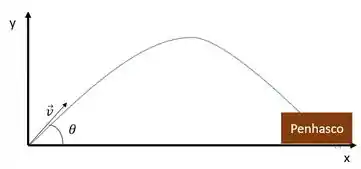
Passo 2
- O y é um movimento uniformemente variado. Para descobrir a altura do penhasco vamos usar
- A altura máxima pode ser descoberta pela fórmula,
Lembrando que
Substituindo
O penhasco tem 25,5 m.
Passo 3
O ponto mais alto a velocidade é zero, substituindo
Assim, a altura máxima é 34,3m
Passo 3
c. Para encontrar o módulo da velocidade faremos em y
Agora em x como é um Movimento Uniforme, a velocidade inicial é igual a velocidade final
Logo
Resposta
a.
b.
c.