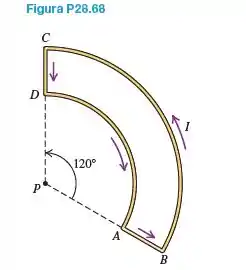
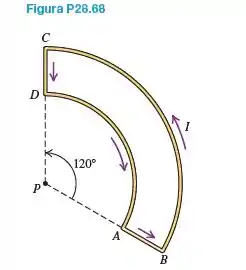
Calcule o campo magnético (módulo, direção e sentido) em um ponto P produzido por uma corrente no fio mostrado na Figura P28.68. O segmento BC é um arco de uma circunferência com raio de 30,0 cm e o ponto P está no centro da curvatura do arco. O segmento DA é um arco de um círculo com raio de 20,0 cm, e o ponto P está em seu centro de curvatura. Os segmentos CD e AB são linhas retas com 10,0 cm de comprimento cada.
Passo 1
E aiii gente, tudo bom com vocês? Vamos fazer mais uma questãozinha aqui! O enunciado pede pra gente achar o valor do campo magnético no ponto P, da figura. Devemos fornecer o módulo, o sentido e a direção desse campo, produzido por um fio meio estranho, na figura.
Pra resolver esse problema, vamos precisar usar a Lei de Biot-Savart, que relaciona o campo magnético gerado por uma corrente com o elemento infinitesimal de fio:
Repare que o produto vetorial só admite contribuições de fios que não sejam paralelos à direção de onde queremos analisar o campo magnético. Em outras palavras, os trechos CD e AD não produzirão campo magnético no ponto P!!
Além disso, o enunciado nos informa que o trecho DA e o trecho BC são arco de círculos, formando um ângulo interno de e raios de e e que a corrente que percorre o fio é de .
Vale lembra que podemos organizar os dados nas unidades convencionais da física:
Com isso tudo organizado, vamos ao ataque!
Passo 2
Primeiro, vamos calcular o campo gerado pelo trecho BC. Aplicando Biot-Savart, temos:
A direção e sentido do campo magnético é determinada pela regra da mão direita. Como o elemento de fio que estamos analisando é perpendicular ao ponto P onde queremos avaliar, então o produto se torna apenas !
Podemos escrever aquele elemento de outra forma
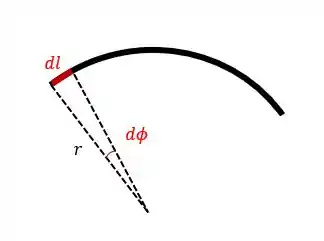
Se a gente analisar bem a figura, podemos ver que o elemento pode ser reescrito como:
Assim, nosso campo magnético será:
Se a gente integrar os dois lados, achamos o campo total do ramo !
Simplificando a expressão e substituindo as informações, temos:
O valor da constante é algo tabelado e conhecido. Seu valor é:
Substituindo esse valor na expressão que obtemos, temos:
O sentido do campo é dado pela regra da mão direita e é no sentido perpendicular da página, ou seja, entrando na página no ponto P!
Passo 3
Para o ramo , vamos fazer o mesmo processo que fizemos anteriormente. Pela expressão de Biot-Savart, temos:
Agora, podemos pular todo o passo a passo já que faremos analogamente. Nosso elemento de comprimento se torna:
O raio dessa vez é:
O fio é percorrido pela mesma corrente. Dessa forma, teremos:
Integrando dos dois lados, temos:
Substituindo o valor da constante, temos:
O sentido do campo é saindo do plano em !
Passo 4
Nosso vetor campo magnético resultante será dado pela soma vetorial dos campos no ponto P. Como temos campos com sentidos opostos, temos o seguinte:
Entrando no plano
Saindo do plano
Como temos:
O campo magnético resultante será no sentido perpendicular do plano, orientado para fora dele, ou seja, saindo do plano !
Seu valor será:
Substituindo os valores:
Vamos deixar os valores nas mesmas potencias para podermos realizar a operação. Com isso, temos:
O valor é:
Prontinho!