Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Young and Freedman - Vol 3- Ed: 14º - Capítulo 21.Exercícios - Ex. 85

Uma carga negativa - Q é distribuída uniformemente ao longo da quarta parte de uma circunferência de raio a , que está sobre o primeiro quadrante, com centro de curvatura na origem. Encontre os componentes x   e   y do campo elétrico na origem.

Passo 1

Olá, tudo bem? Vou ajudar você aqui!

A ideia aqui é dividir esse pedaço de fio em pedacinhos e ver o diferencial de campo produzido por esse pedacinho. Depois integrar sobre todo o fio, vamos começar?

Vamos começar com um desenho:

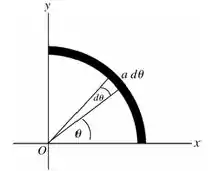
d θ o comprimento de arco correspondente é a d θ . E nesse pedaço de fio temos a seguinte quantidade de carga:

d q = a d θ 1 2 π a q = 2 q π d θ

E o diferencial de campo é:

d E = 1 4 π ϵ 0 . d q a 2 = q 2 π 2 ϵ 0 a 2 d θ

Passo 2

Agora vamos ver a decomposição do vetor campo elétrico. Nesse fio, o campo elétrico aponta sempre para dentro, na direção radial, da seguinte forma:

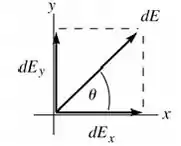
Assim o diferencial de campo elétrico pode ser escrito nas componentes x e y :

d E x = d E   c o s θ

d E y = d E   s e n θ

Sendo que θ varia entre 0 ≤ θ ≤ π / 2 .

Agora é só juntar tudo isso e integrar! Vamos lá?

Passo 3

Primeiro em x :

E x = ∫ 0 π / 2 d E   c o s θ = ∫ 0 π / 2 q 2 π 2 ϵ 0 a 2 c o s θ d θ

E x = q 2 π 2 ϵ 0 a 2 . s e n θ 0 π / 2 = q 2 π 2 ϵ 0 a 2

E agora em y :

E y = ∫ 0 π / 2 d E   s e n θ = ∫ 0 π / 2 q 2 π 2 ϵ 0 a 2 s e n θ d θ

E y = q 2 π 2 ϵ 0 a 2 . - c o s θ 0 π / 2 = q 2 π 2 ϵ 0 a 2

Assim as componentes desse campo na origem são:

E x = E y = q 2 π 2 ϵ 0 a 2

Resposta

E x = E y = q 2 π 2 ϵ 0 a 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Na Fig. 24-34, duas barras finas de plástico, uma de carga +q e a outra de carga −q, formam um círculo de raio R num plano xy. Um eixo x passa pelos pontos que unem as duas barras e a carga em cada um
Uma barra fina, não-condutora, de comprimento finito L, tem uma carga q uniformemente distribuída ao longo dela. Mostre que o módulo E do campo elétrico no ponto P sobre a mediatriz da barra é dado po
Um elétron tem seu movimento restrito ao eixo central do anel de carga de raio R discutido na Seção 24-6. Mostre que a força eletrostática exercida sobre o elétron pode fazê-lo oscilar através do cent
Na Fig. 24-37, uma barra não-condutora, de comprimento L, tem uma carga -q uniformemente distribuída ao longo de seu comprimento. (a) Qual a densidade linear de carga da barra? (b) Qual o campo elétri
Uma barra fina de vidro e encurvada na forma de um semicírculo de raio r. Uma carga +Q está distribuída uniformemente ao longo da metade superior, e uma carga −Q, distribuída uniformemente ao longo da