Exercícios de Campo Elétrico Gerado por uma Linha de Cargas - Lista de Exercícios Resolvida
Questão 1
Na figura abaixo, uma barra fina de vidro forma uma semicircunferência de raio .
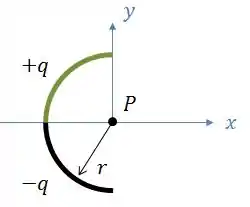
Uma carga está distribuída uniformemente na metade superior da barra, e uma carga está distribuída uniformemente na metade inferior.
Determine:
- O módulo do campo elétrico no ponto , situado no centro do semicírculo.
- A orientação (em relação do semi-eixo positivo) do campo elétrico no ponto , situado no centro do semicírculo.
Questão 2
Uma barra isolada, de comprimento , tem uma carga distribuída uniformemente ao longo de sua extensão, conforme a figura.

Determine o vetor campo elétrico no ponto , situado a uma distância da extremidade direita da barra;
Suponha que uma outra carga isolada puntiforme seja colocada num outro ponto distante da extremidade direita da barra. Determine o vetor campo elétrico no ponto devido apenas à carga isolada;
Determine, agora, o vetor campo elétrico total no ponto ;
Ver solução completaQuestão 3
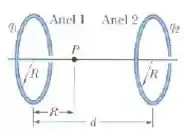
A figura abaixo mostra dois anéis não condutores paralelos, com os centros sobre a mesma reta perpendicular aos planos dos anéis. O anel , de raio , possui uma carga uniforme ; O anel , também de raio , possui uma carga uniforme ; Os anéis estão separados por uma distância . O campo elétrico no ponto situado na reta que passa pelos centros dos anéis a uma distância do anel é zero. Determine a razão .
Questão 4
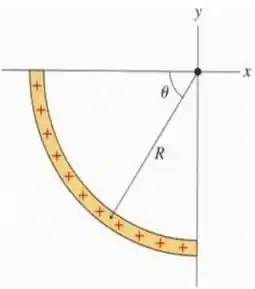
Na figura abaixo, uma barra não condutora “semi-infinita” (ou seja, infinita apenas em um sentido) possui uma densidade linear de cargas uniforme .

Mostre que o campo elétrico no ponto faz um ângulo de com a barra e que esse resultado não depende da distância .
(Sugestão: Calcule separadamente as componentes de nas direções paralela e perpendicular à barra.)
Ver solução completaQuestão 5
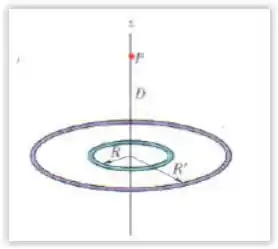
A figura abaixo mostra dois anéis concêntricos de raios e , que estão no mesmo plano. O ponto está no eixo central , a uma distância do centro dos anéis. O anel menor possui carga uniforme distribuída . Em termos de , qual deve ser a carga uniformemente distrubuída no anel maior para que o campo elétrico no ponto seja nulo?
Questão 6
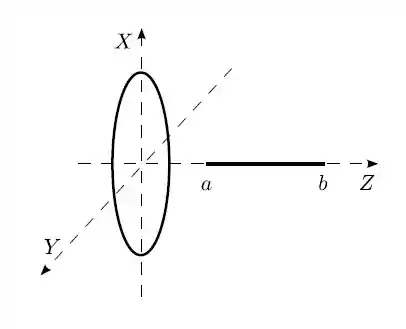
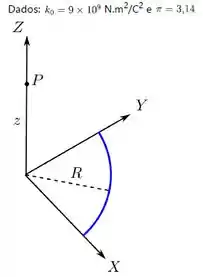
Um anel circular, muito fino, de raio , encontra-se em repouso no plano , com seu centro na origem. Tal anel possui carga total , uniformemente distribuída.
- Calcule o vetor campo elétrico (módulo, direção e sentido) devido a tal anel num ponto do eixo , com cota arbitrária .
- Considere agora um bastão retilíneo, muito fino, em repouso, situado no eixo , entre e . Tal bastão também possui carga total , uniformemente distribuída. Calcule o vetor força elétrica sobre tal bastão devido ao anel. (Sugestão: a força sobre o bastão constitui-se da soma vetorial das forças sobre cada elemento infinitesimal do bastão carregado).
Questão 7
Um elétron é liberado a partir do repouso no eixo central de um disco uniformemente carregado de raio . A densidade superficial de cargas do disco é . Determine o módulo da aceleração inicial do elétron se ele for liberado a uma distância do centro do disco de:
(a)
(b)
(c)
(d) Por que o módulo da aceleração quase não varia com a distância entre a carga e o disco?
Dado: Razão carga massa do elétron:
Ver solução completaQuestão 8
Uma barra isolada, de comprimento , tem uma carga distribuída uniformemente ao longo de sua extensão, conforme a figura.
Determine o vetor campo elétrico no ponto , situado a uma distância da extremidade direita da barra;
Suponha que uma outra carga isolada puntiforme seja colocada num outro ponto distante da extremidade direita da barra. Determine o vetor campo elétrico no ponto devido apenas à carga isolada;
Determine, agora, o vetor campo elétrico total no ponto ;
Ver solução completaQuestão 9
Um engenheiro foi encarregado de projetar um dispositivo no qual um disco uniformemente carregado de raio produz em um ponto sobre o eixo do disco a uma distância do plano do disco. Para economizar material decidiu-se substituir o disco por um anel com o mesmo raio externo e um raio interno . O anel tem a mesma densidade superficial de cargas que o disco original. Qual é a razão entre o novo campo no ponto e o campo antigo?
Questão 10
Uma barra delgada de comprimento é envergada até formar um semi-círculo, conforme mostra a Figura 1.
Se a barra tem uma densidade de carga uniforme , calcule o campo elétrico na origem.
Onde deveria ser colocada uma carga pontual de valor igual ao da carga total da barra para que o campo na origem fosse nulo?
Considere agora que esse semicírculo se torne um semi-disco de mesmo raio com um orifício concêntrico semicircular de raio e com uma densidade superficial uniforme , como mostrado na Figura 2. Calcule o campo elétrico na origem devido a esta nova configuração.
Ver solução completaQuestão 11
Um anel circular, muito fino, de raio , encontra-se em repouso no plano , com seu centro na origem. Tal anel possui carga total , uniformemente distribuída.
- Calcule o vetor campo elétrico (módulo, direção e sentido) devido a tal anel num ponto do eixo , com cota arbitrária .
- Considere agora um bastão retilíneo, muito fino, em repouso, situado no eixo , entre e . Tal bastão também possui carga total , uniformemente distribuída. Calcule o vetor força elétrica sobre tal bastão devido ao anel. (Sugestão: a força sobre o bastão constitui-se da soma vetorial das forças sobre cada elemento infinitesimal do bastão carregado).
Questão 12
A figura abaixo mostra dois anéis concêntricos de raios e , que estão no mesmo plano. O ponto está no eixo central , a uma distância do centro dos anéis. O anel menor possui carga uniforme distribuída . Em termos de , qual deve ser a carga uniformemente distrubuída no anel maior para que o campo elétrico no ponto seja nulo?
Questão 13
A que distância do eixo de um disco de plástico uniformemente carregado de de raio o módulo do campo elétrico é igual à metade do módulo do campo no centro do disco?
Questão 14
Uma barra delgada de comprimento é envergada até formar um semi-círculo, conforme mostra a Figura 1.
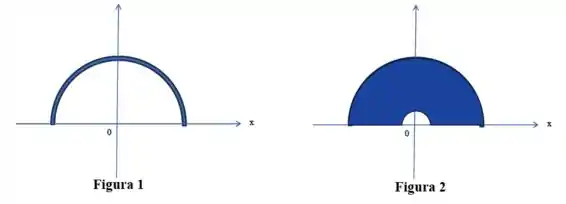
Se a barra tem uma densidade de carga uniforme , calcule o campo elétrico na origem.
Onde deveria ser colocada uma carga pontual de valor igual ao da carga total da barra para que o campo na origem fosse nulo?
Considere agora que esse semicírculo se torne um semi-disco de mesmo raio com um orifício concêntrico semicircular de raio e com uma densidade superficial uniforme , como mostrado na Figura 2. Calcule o campo elétrico na origem devido a esta nova configuração.
Ver solução completaQuestão 15
Um fio de comprimento está alinhado com o eixo e carregado uniformemente com uma densidade linear de carga . Determine uma expressão para o vetor campo elétrico em um ponto arbitrário do eixo , conforme mostra a Figura 1.
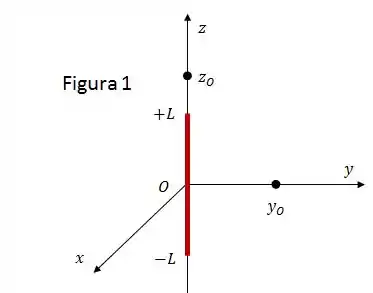
Determine agora uma expressão para o vetor campo elétrico em um ponto arbitrário do eixo , para o mesmo fio do item e da Figura 1.
Considere agora dois fios de lados paralelos ao eixo , simetricamente dispostos em relação ao mesmo, afastados entre si da distância e carregados uniformemente com a densidade linear de carga , conforme mostra a Figura 2.
Utilize, adaptando-a, a solução do item para determinar o vetor campo elétrico devido aos fios num ponto arbitrário do eixo .
Questão 16
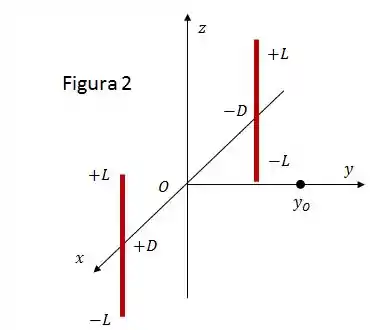
Um anel isolante delgado de raio com densidade linear de carga uniforme encontra-se no plano . O eixo passa pelo centro do anel, coincidente com a origem dos eixos (Figura 1).
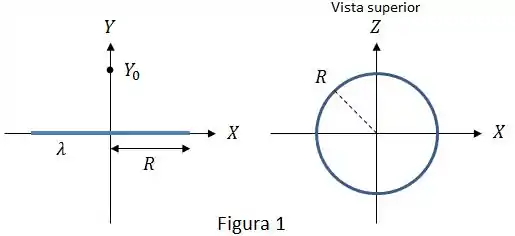
Calcule o vetor campo elétrico (módulo, direção e sentido) gerado pelo anel delgado num ponto qualquer sobre do eixo . Chame de a coordenada deste ponto ao longo do eixo Y.
Considere agora que o anel delgado é substituído por uma calha cilíndrica com base circular de raio , altura e densidade superficial de carga não uniforme. Como indicado na Figura 2, o plano corta a calha no plano mediano dela.
A partir do resultado do item calcule o campo elétrico (módulo, direção e sentido) gerado pela calha no ponto , considerando .
(Deixe o resultado em função dos símbolos das grandezas e parâmetros físicos)
Ver solução completaQuestão 17
Três anéis circulares, de mesmo raio, cujos quadrantes foram carregados uniformemente com cargas positivas e negativas, de mesmo módulo, estão representados na figura abaixo. Considere as seguintes afirmações: (A) o campo elétrico no centro do anel I é nulo; (B) o campo elétrico no centro do anel II tem direção e sentido de ; (C) o campo elétrico no centro do anel III tem direção e sentido de .
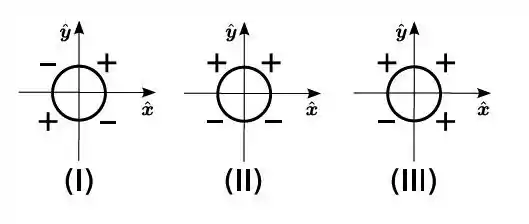
- Somente a afirmação A está correta.
- Somente a afirmação B está correta.
- Somente a afirmação C está correta.
- Somente as afirmações A e B estão corretas.
- Somente as afirmações A e C estão corretas.
- Somente as afirmações B e C estão corretas
- Todas as três afirmações (A, B e C) estão corretas.
Questão 18
Um anel circular, muito fino, de raio , encontra-se em repouso no plano , com seu centro na origem. Tal anel possui carga total , uniformemente distribuída.
- Calcule o vetor campo elétrico (módulo, direção e sentido) devido a tal anel num ponto do eixo , com cota arbitrária .
- Considere agora um bastão retilíneo, muito fino, em repouso, situado no eixo , entre e . Tal bastão também possui carga total , uniformemente distribuída. Calcule o vetor força elétrica sobre tal bastão devido ao anel. (Sugestão: a força sobre o bastão constitui-se da soma vetorial das forças sobre cada elemento infinitesimal do bastão carregado).
Questão 19
Considere uma barra finita de comprimento , com densidade linear de carga uniforme .
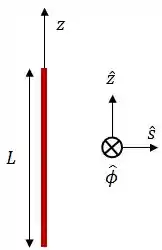
Qual das afirmativas abaixo é verdadeira?
O campo elétrico sempre aponta na direção .
O campo elétrico só depende da coordenada .
A direção do campo elétrico independe da coordenada .
O módulo do campo elétrico independe da coordenada .
O módulo do campo elétrico independe da coordenada .
O módulo do campo elétrico independe da coordenada .
Ver solução completaQuestão 20
Dois fios retilíneos de comprimento , carregados com densidades lineares de carga e , são conectados por um fio semicircular de raio , uniformemente carregado com densidade de carga .
Devido ao campo elétrico resultante em , uma carga eletrica abandonada neste ponto é ejetada formando um ângulo com a direção dos dois fios retilíneos.
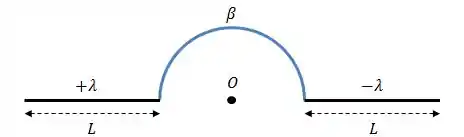
Dados: e
Determine o campo elétrico em devido a distribuição de cargas ;
Calcule a componente vertical do campo elétrico em devido a distribuição de cargas ;
Com os valores de e , determine a densidade linear em função de , e ;
Ver solução completaQuestão 21
A figura abaixo mostra dois arcos de circunferência cujo centro está na origem de um sistema de coordenadas. Em cada arco a carga está uniformemente distribuída.
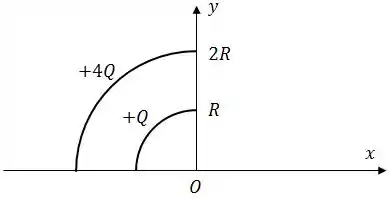
Determine:
O vetor campo elétrico para cada arco na origem;
O vetor campo elétrico total na origem (dê a sua orientação em relação ao semi-eixo positivo);
Ver solução completaQuestão 22
Considere um anel circular, muito fino, de raio , com uma carga total distribuída, uniformemente (e estacionariamente) ao longo dele. O anel está no plano cartesiano (ou seja, plano ), com o eixo pelo centro do anel. Qual é o vetor campo elétrico num ponto situado no eixo
Questão 23
Uma barra fina isolante de comprimento é posicionada sobre o eixo de um sistema de coordenadas com seu centro sobre a origem, como mostrado abaixo. Ela encontra-se carregada de forma que a porção possui uma densidade linear constante , e na porção uma densidade . Considere os pontos e indicados na figura. Podemos afirmar que o campo elétrico produzido pela barra nestes pontos aponta, respectivamente, no sentido dos vetores:
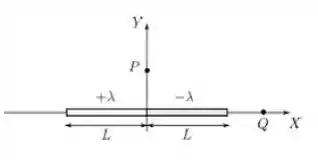
Escolha uma:
Questão 24
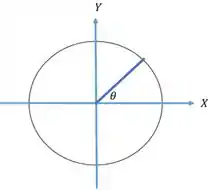
Considere um anel circular fino, de raio , com centro na origem de um sistema de coordenadas cartesianas, situado no plano . Tal anel possui uma densidade linear de carga elétrica dada por:
Onde é o usual ângulo polar medido a partir do eixo , tal como mostra a figura. Qual é o campo elétrico no centro do anel.
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 25
Em um fio muito longo de raio R, centrado ao longo do eixo z, passa uma corrente I (no sentido de z positivo). A corrente elétrica está distribuída no fio de tal forma que a densidade de corrente é dada por na região 0 ≤ r ≤ R, onde K é uma constante positiva.
(a) (0,5 ponto) Determine a dimensão da constante K no sistema internacional de unidades.
(b) (1,0 ponto) Determine a corrente total I que passa pelo fi o. Expresse sua resposta em termos de K e R.
(c) (1,0 ponto) Encontre o vetor campo magnético nas regiões 0 ≤ r ≤ R e r > R.
Expresse sua resposta em termos de K, R, e r.
Ver solução completaQuestão 26
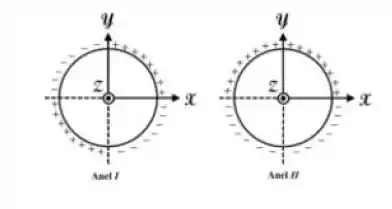
Dois anéis circulares finos, de mesmo raio, cujos quadrantes carregados uniformemente com cargas positivas e negativas, de mesmo módulo, como mostra a figura. O que se pode afirmar sobre o campo elétrico resultante no centro desses anéis?
Escolha uma:
- O campo elétrico no centro do anel I é nulo e do anel II tem direção e sentido .
- O campo elétrico no centro do anel I tem direção e sentido e no centro do anel II tem direção e sentido
- O campo elétrico no centro do anel I é nulo e do anel II tem direção e sentido .
- O campo elétrico no centro do anel I é nulo e do anel II tem direção e sentido .
- O campo elétrico no centro do anel I tem direção e sentido e no centro do anel II tem direção e sentido
Questão 27
A estrutura ilustrada na figura abaixo é composta por três barras isolantes, uma semicircular de raio , e duas retilíneas e que são perpendiculares entre si. As três barras apresentam uma densidade linear de carga constante e positiva . O ponto é o centro do semicírculo e a origem do sistema de coordenadas -.
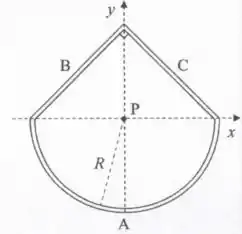
- Calcule o vetor campo elétrico produzido apenas pela barra semicircular no ponto .
- Calcule o vetor campo elétrico produzido por ambas as barras retilíneas e , no ponto .
- Se colocamos uma carga pontual negativa no ponto , em que direção e sentido esta carga vai se mover? Explique sua resposta.
Dado:
Ver solução completaQuestão 28
Uma barra isolante fina, de comprimento é posicionada sobre o eixo de um sistema de coordenadas com seu centro sobre a origem. Ela está uniformemente carregada e possui uma carga total igual a . Considere um ponto sobre o eixo , localizado a uma distância da origem. Qual é o módulo do campo elétrico produzido pela barra neste ponto?
Escolha uma:
Questão 29
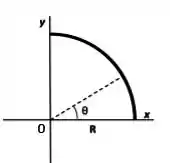
O arco de um quarto de circunferência de raio , mostrado na figura abaixo, possui uma distribuição de carga não uniforme dada por , sendo uma constante positiva.
(a) Calcule a carga total presente no arco, em função de e de .
(b) Calcule (em função de , de e da constante de Coulomb ) as componentes e com os respectivos sinais, do vetor campo elétrico criado pelo arco sobre o ponto localizado na origem.
Considere agora que o arco gere, em um ponto qualquer, um campo elétrico e que neste mesmo ponto seja colocada uma carga puntiforme .
(c) Encontre o vetor da força elétrica exercida pelo arco sobre a carga.
Questão 30
Um fio isolante fino tem a forma de um quarto de círculo de raio . Ele está posicionado sobre o primeiro quadrante do plano de um sistema de coordenadas com centro na origem, como mostra a figura abaixo. Sabendo que o fio possui uma carga total uniformemente distribuída ao longo de seu comprimento, qual é o valor aproximado da componente do campo elétrico produzido por ele em um ponto localizado sobre o eixo , a uma distância do centro?
Questão 31
Na figura abaixo duas barras isolantes muito finas, ambas de comprimento , estão uniformemente carregadas. Uma das barras possui carga e a outra barra possui carga desconhecida. As barras estão posicionadas em direções perpendiculares, conforme a figura.
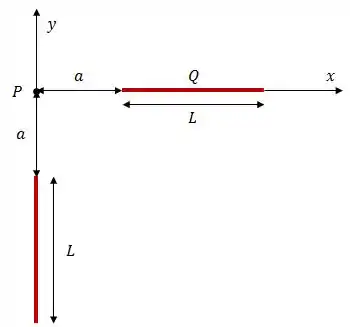
Determine o vetor campo elétrico (módulo, direção e sentido) no ponto produzido pela barra de carga ;
Sabendo que ao colocar uma partícula carregada positivamente em , a força exercida sobre esta faz um ângulo de com o eixo , calcule a componente do campo elétrico total;
Determine a densidade linear de carga da barra cuja carga é desconhecida;
Ver solução completaQuestão 32
. Um anel circular fino, isolante, de raio é posicionado sobre o plano de um sistema de coordenadas com seu centro sobre a origem. Ele encontra-se uniformemente carregado e possui carga total . Uma barra fina, isolante, de comprimento é posicionada sobre o eixo positivo com sua extremidade mais próxima do anel a uma distância da origem. A barra também encontra-se uniformemente carregada e possui carga total . Nessa situação, qual é o módulo da força elétrica que o anel exerce sobre a barra?
Sugestão: Divida a barra em elementos infinitesimais de carga e considere a força que o campo elétrico gerado pelo anel exerce sobre cada elemento.
Dado: O campo elétrico produzido pelo anel em pontos sobre o eixo é dado por:
Escolha uma opção:
Ver solução completaQuestão 33
Considere os dois semicírculos concêntricos de material isolante representados na figura abaixo. O semicírculo com raio tem densidade linear de carga positiva , enquanto o semicírculo menor tem raio e duas densidades lineares de carga: (positiva) para pontos com coordenada negativa e (negativa) para pontos com coordenada positiva. Os raios e as densidades lineares das duas distribuições de carga são tais que vale a relação .
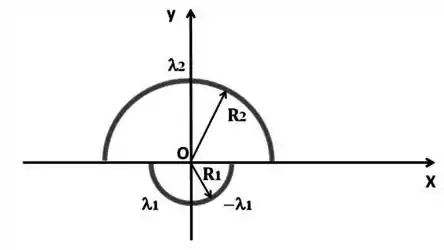
Calcule o vetor campo elétrico gerado pelo semicírculo menor no ponto (origem dos eixos e centro dos semicírculos)
Calcule o vetor campo elétrico gerado pelo semicírculo maior no ponto .
Calcule o vetor de campo elétrico resultante do ponto e escreva seu módulo.
Calcule as coordenadas da posição na qual deve ser colocada uma carga puntiforme negativa de valor , para que o campo elétrico total resultante no ponto seja nulo.
Ver solução completaQuestão 34
Um fio de comprimento (com extremidades localizadas nos pontos e do eixo ) está carregado com uma densidade de carga uniforme . Todos os pontos de interesse para o problema estão localizados no plano ().
- Calcule o campo elétrico gerado pelo fio carregado em pontos do eixo , para e para .
- Calcule o potencial elétrico gerado pelo fio carregado em pontos do eixo , para e para .
- Encontre o valor do campo elétrico no ponto para .
- Calcule a aceleração da partícula quando ela está em alguma posição .
- Calcule a velocidade final da partícula carregada quando ela está a uma distância muito grande do fio.
Uma partícula de carga e massa é então colocada em com velocidade inicial nula. Ela se move apenas sob a ação da força eletrostática repulsiva devido ao fio. Ignore efeitos gravitacionais.
Questão 35
Uma barra isolante fina de comprimento é posicionada sobre o eixo de um sistema de coordenadas com seu centro sobre a origem, como mostrado na figura abaixo. Ela encontra-se carregada de forma que a porção possui uma densidade linear de carga constante e a porção possui uma densidade linear constante . Considere os pontos e indicados na figura. Podemos afirmar que o campo elétrico produzido pela barra nestes pontos aponta, respectivamente, no sentido dos vetores:
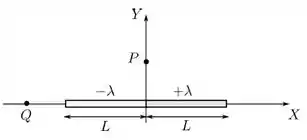
a) e
b) e
c) e
d) e
e) e
f) e
g) e
h) e
Ver solução completaQuestão 36
Uma carga positiva é distribuída uniformemente na metade inferior de uma haste e uma carga negativa é distribuída uniformemente na metade superior. Qual é a orientação do campo elétrico em um ponto sobre a mediatriz do segmento de reta que liga as duas cargas?
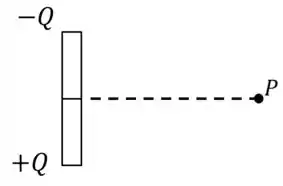
a)
b)
c)
d)
e) zero
Ver solução completaQuestão 37
A figura abaixo mostra um sistema formado por quatro fios retilíneos de mesmo comprimento e um anel de raio . Os fios formam um quadrado com centro geométrico no ponto , que fica também no centro do anel. As linhas azuis contínuas representam distribuições lineares de carga positiva e as linhas azuis tracejadas representam também uniformes com densidade linear . Sendo o módulo do campo elétrico resultante no ponto , qual o vetor do campo elétrico nesse ponto?
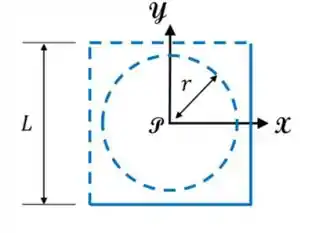
Escolha uma:
Questão 38
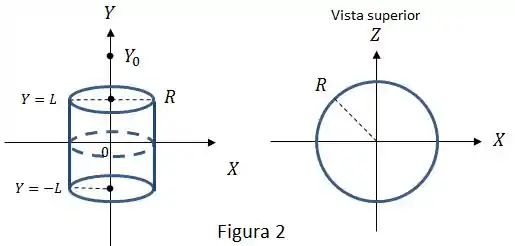
Considere um anel circular, fino de raio , com uma distribuição de carga linear, estacionária, com carga total . O campo elétrico, devido a tal anel em um ponto de seu eixo perpendicular de simetria, com cota , definida a partir do centro do anel (conforme a Figura 1), é dado por:
Considere, agora, uma superfície cilíndrica (aberta, ou seja, sem incluir as bases) circular, reta, de raio , e comprimento (ou altura) , com uma densidade superficial constante (homogênea e estacionária) (conforme a Figura 2).
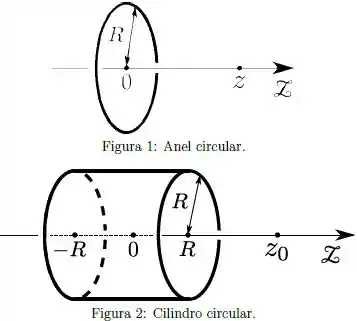
Determine a carga total do tal cilindro.
Supondo que tal cilindro é coaxial com o eixo , com seu plano médio coincidente com o plano (conforme a Figura 2), determine o campo elétrico em um ponto do eixo , com cota .
Encontre o limite assintótico do campo do cilindro determinado no item (dependência do campo com ), para . Discuta o resultado encontrado.
Ver solução completaQuestão 39
A figura abaixo mostra uma barra retilínea não condutora de comprimento , com carga elétrica uniformemente distribuída.

Qual é a densidade linear de carga da barra?
Calcule o vetor campo elétrico produzido no ponto , situado no eixo , a uma distância da extremidade direita da barra, em termos das variáveis dadas no problema.
Considere que no ponto seja colocado um dipolo elétrico, de momento de dipolo elétrico de módulo , formando um ângulo de com o eixo positivo. Calcule a energia potencial do dipolo.
Ver solução completaQuestão 40
Duas hastes plásticas, carregadas uniformemente com cargas e formam um anel de
raio como mostra a figura abaixo. A intensidade, direção e sentido do campo elétrico no centro do anel (ponto C) é:

- , horizontal apontando para esquerda
- , horizontal apontando para direita
- , horizontal apontando para esquerda
- , horizontal apontando para esquerda
Questão 41
A figura mostra uma barra não-condutora com uma densidade linear de carga positiva distribuída uniformemente ao longo de seu comprimento. A barra é dobrada em uma semicircunferência de raio .
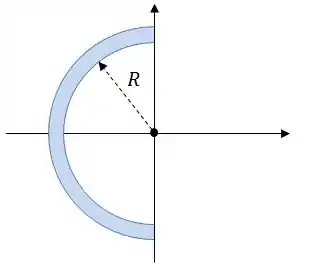
O módulo do campo elétrico no centro da semicircunferência é:
Ver solução completa
Questão 42
Quatro fios finos de mesmo comprimento estão dispostos no plano simetricamente em torno da origem, como mostrado na figura abaixo. Cada um dos fios dispostos ao longo do eixo possui uma carga , estacionária e uniformemente distribuída. Já os fios dispostos ao longo do eixo possuem, cada um, uma carga , também estacionária a uniformemente distribuída.
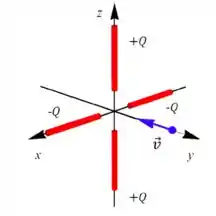
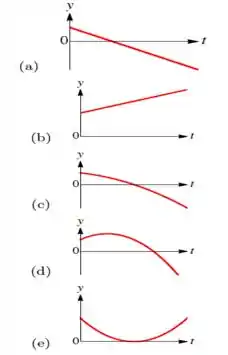
No instante de tempo , uma partícula de carga encontra-se sobre o eixo , deslocando-se com velocidade . Dentre os gráficos abaixo, qual deles descreve o movimento subsequente da partícula?
Questão 43
Seja a carga por unidade de comprimento distribuída uniformemente ao longo de um segmento de reta de comprimento .

Determine:
- O vetor campo elétrico em um ponto , situado a uma distância de uma das extremidades do segmento carregado, e situado sobre o seu prolongamento;
- A aceleração que uma partícula, de massa e carga , sofre quando colocada no ponto .
Questão 44
Dois fios retilíneos de mesmo comprimento , separados por uma distância , estão uniformemente carregados com densidades lineares de carga e . Considerando o sistema de coordenadas abaixo, calcule:
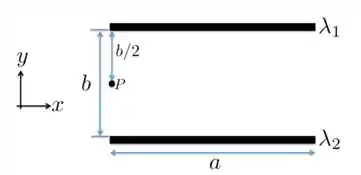
- O vetor campo elétrico no ponto ;
- O potencial elétrico no ponto ;
- O trabalho que um agente externo deve realizar sobre uma carga para trazê-la desde o infinito até o ponto .
Questão 45
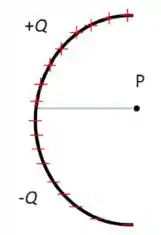
Uma carga positiva está uniformemente distribuída na metade superior do semicírculo e uma carga negativa está distribuída na metade inferior, como mostrado na figura abaixo. Qual é a direção e sentido do campo elétrico no ponto (o ponto está no centro do semicírculo)?
Questão 46
Um plano condutor infinito e aterrado, ou seja, mantido a um potencial eletrostático zero, é posicionado sobre o plano de um sistema de coordenadas. Uma partícula de carga é posicionada sobre o eixo , na porção , a uma distância do plano, como mostrado na figura abaixo. Sabe-se que, quando o sistema partícula plano está em equilíbrio eletrostático, o campo eletrostático na região é idêntico ao produzido por outro sistema onde o plano é substituído por uma segunda partícula, de carga , colocada na posição correspondente à imagem especular da primeira partícula com relação ao plano.l
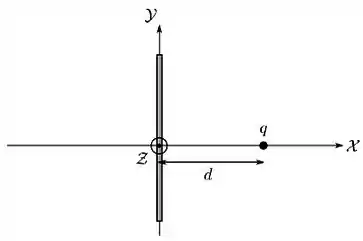
(a) Determine a força eletrostática (módulo, direção e sentido) que o plano exerce sobre a partícula.
(b) Determine o campo eletrostático (módulo, direção e sentido) produzido pelo sistema partícula plano em um ponto arbitrário sobre o plano , a uma distância da origem. Considere que este ponto está na vizinhança externa do plano na porção .
(c) Utilizando o resultado do item anterior, determine a densidade superficial de carga induzida sobre o plano no ponto . Interprete o resultado.
Ver solução completaQuestão 47
Parte ) Considere uma esfera isolante, que está mostrada na figura abaixo, de raio e densidade volumétrica de carga , onde é a carga total da esfera isolante. Utilizando a lei de Gauss,
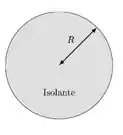
- Determine o campo elétrico na região .
- Determine do campo elétrico na região .
- Determine o campo elétrico na região .
- Determine o campo elétrico na região .
Parte ) Uma esfera isolante de raio foi envolta por uma casca esférica condutora de carga líquida nula. Essa casca esférica, em equilíbrio eletrostático, possui raio interno e raio externo , como mostra a figura abaixo. Nesta situação, considere que a carga total da esfera isolante é , distribuída uniformemente no seu interior.
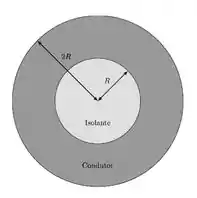
Questão 48
Um fio isolante fino é dobrado na forma de de circunferência, como mostrado na figura abaixo. Seu centro coincide com a origem do sistema de coordenadas e ele se encontra carregado de forma que as porções no primeiro, segundo e quarto quadrantes estão uniforme e estacionariamente carregados com densidades lineares , e , respectivamente ().
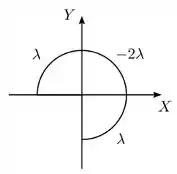
Nessa situação, podemos afirmar que o campo elétrico produzido pelo fio na origem aponta no mesmo sentido do vetor:
- O campo elétrico é nulo neste ponto.
Questão 49
A figura ao lado ilustra uma esfera oca não-condutora de raio interno e raio externo que tem densidade volumétrica de carga variável para , onde é uma constante positiva e denota a distância radial ao centro da esfera. Tal esfera está localizada no vácuo, cuja constante de permissividade elétrica é dada por . Nestas condições, calcule:
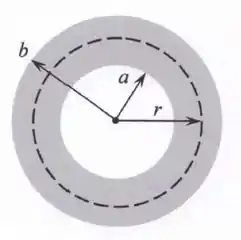
- A carga elétrica total da esfera oca.
- O módulo do campo elétrico para .
- O módulo do campo elétrico para .
- O módulo do campo elétrico para .
Questão 50
Um fio e um plano, ambos infinitos, carregados eletricamente, são posicionados paralelamente como ilustrado na figura.
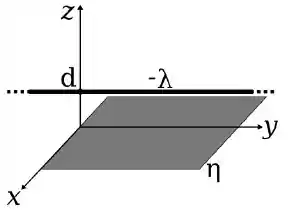
As densidades de carga do fio e do plano valem e , respectivamente, onde e são números positivos. O local onde a intensidade do campo elétrico resultante é nulo:
se localiza em um outro plano (paralelo ao plano carregado) que cruza o eixo na posição .
se localiza ao longo de outra reta (paralela ao fio) que cruza o eixo na posição .
se localiza em um outro plano (paralelo ao plano carregado) que cruza o eixo na posição .
se localiza ao longo de outra reta (paralela ao fio) que cruza o eixo na posição .
se localiza ao longo de outra reta (paralela ao fio) que cruza o eixo na posição .
Ver solução completaQuestão 51
a) Um anel isolante, delgado de raio , possui uma distribuição uniforme de carga positiva . Calcule o vetor campo elétrico num ponto situado no eixo, a uma distância do plano anel.
b) Um disco isolante de raio tem uma densidade superficial de carga positiva variável , onde é uma constante positiva e a distância radial medida desde o centro do disco. Calcule o vetor campo elétrico no ponto do eixo do disco à uma distância do seu plano (ver figura abaixo).
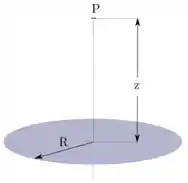
Questão 52
Uma partícula de carga é colocada do lado de fora de uma grande camada esférica condutora neutra. Em qualquer ponto do interior da camada, o campo elétrico produzido pelas cargas superficiais da camada aponta
- para a carga ;
- para longe da carga ;
- para a superfície;
- para longe da superfície;
- nenhuma das alternativas.
Questão 53
11 - Considere um plano infinito, uniformemente carregado, coincidente com o plano XY e um dado sistema de coordenadas. Sobre o campo elétrico produzido por este plano, considere as afirmativas abaixo:
- é independente das coordenadas x e y.
- A direção de é paralela ao eixo Z em todos os pontos do espaço.
- aponta no mesmo sentido em todos os pontos do espaço.
São VERDADEIRAS as afirmativas:
- Apenas II
- Apenas I e III
- Apenas III
- I, II e III
- Apenas I e II
Questão 54
Uma linha uniforme de cargas de comprimento e a carga total produz um campo elétrico a uma distância da linha ao longo da sua mediatriz que é dado pela equação: .
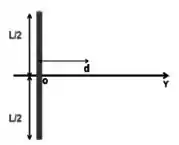
Considere agora um sistema constituído por uma calha cilíndrica isolante de comprimento , raio de curvatura , carregada uniformemente com carga total positiva. A origem dos eixos está situada sobre o eixo da calha, a uma distância da superfície lateral da mesma, e no plano mediano que corta a calha em duas partes idênticas de comprimento . A interseção da calha com o plano descreve um arco de circunferência de ângulo igual a , com , como representado na figura.
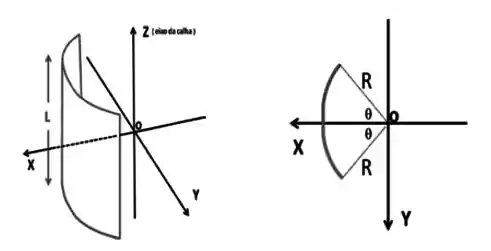
Considere a calha como constituída por fios de carga infinitesimal , largura e comprimento . Calcule a carga infinitesimal de cada fio. (A densidade superficial de carga da calha é )
Considerando que , obtenha o módulo, direção e sentido do campo elétrico gerado pela calha carregada na origem dos eixos .
Um plano infinito carregado uniformemente é agora colocado paralelamente ao plano cortando o eixo na coordenada . Nesta condição, nota-se que o campo elétrico resultante na origem é nulo.
Calcule a densidade superficial de carga do plano infinito carregado.
Ver solução completaQuestão 55
Dois bastões idênticos, finos, de mesmo comprimento , estão dispostos nos semi-eixos positivos e conforme mostra a figura. Neles, há uma distribuição de carga estacionária, não necessariamente uniforme, com a mesma densidade linear, onde é a distância de um ponto genérico sobre um dos bastões até a origem.
Considere dois elementos infinitesimais, nos pontos e , dos bastões em e , com comprimentos e , respectivamente.
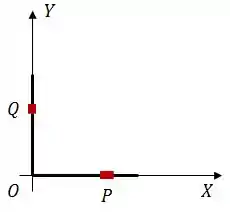
Qual é a força elétrica que o elemento em exerce sobre o elemento em ?
Ver solução completaQuestão 56
Dois estudantes A e B usam diferentes cargas de teste para medir o campo elétrico produzido por uma distribuição de cargas. O estudante B utiliza uma carga de teste que é (em módulo) duas vezes maior do que a carga utilizada pelo estudante A. Nesta situação, o estudante A acha um valor de campo que é:
- O mesmo encontrado pelo estudante B.
- Duas vezes maior que o encontrado pelo estudante B.
- Duas vezes menor que o encontrado pelo estudante B.
- Quatro vezes maior que o encontrado pelo estudante B.
- Quatro vezes menor que o encontrado pelo estudante B.
Questão 57
Uma barra fina, de comprimento , é posicionada ao longo do eixo de um sistema de coordenadas com seu centro sobre a origem, como mostra a figura abaixo. A barra está uniformemente carregada e possui carga total . Considere um elemento de carga infinitesimal da barra localizado no ponto como mostra a figura. Este elemento ocupa uma porção de comprimento infinitesimal da barra. Considere ainda o ponto localizado sobre o eixo . Qual é a expressão da componente vertical do campo elétrico infinitesimal produzido por no ponto ?
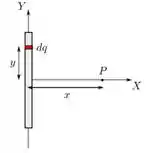
Questão 58
Uma carga positiva é distribuída uniformemente na metade inferior de uma haste e uma carga negativa é distribuída uniformemente na metade superior. Qual é a orientação do campo elétrico em um ponto sobre a mediatriz do segmento de reta que liga as duas cargas?
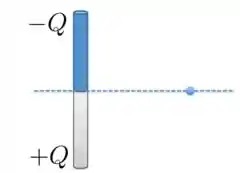
- ;
- ;
- ;
- ;
- zero .
Questão 59
Considere um disco de raio , com densidade superficial de carga uniforme . Seja ainda o sistema de coordenadas cilíndricas usual, e os vetores unitários correspondentes. Sabendo-se que a origem desse sistema está no centro do disco e o eixo é o eixo de simetria, qual das afirmativas abaixo é verdadeira?
O campo elétrico sempre aponta na direção .
O campo elétrico só depende da coordenada .
A direção do campo elétrico independe da coordenada .
O módulo do campo elétrico independe da coordenada .
A direção do campo elétrico independe da coordenada .
O módulo do campo elétrico independe da coordenada .
Ver solução completaQuestão 60
A figura abaixo mostra um anel fino de plástico e raio com uma carga uniformemente distribuída.
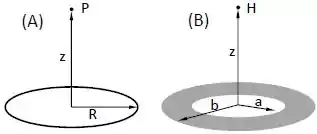
Qual a direção do campo elétrico no ponto da figura , a uma distância do centro do anel ao longo do seu eixo? Justifique sua resposta.
Determine o módulo do campo elétrico no ponto da figura .
A figura mostra um anel de raios interno e externo e , respectivamente. O anel tem densidade superficial de carga uniforme, . Determine o módulo do campo elétrico no ponto , que se encontra sobre o eixo do anel, a uma distância do seu centro.
Dado:
Ver solução completaQuestão 61
Um semianel fino, isolante, de raio é posicionado sobre os dois primeiros quadrantes do plano de um sistema de coordenadas com seu centro sobre a origem, como mostrado na figura abaixo. Ele encontra-se carregado com densidade linear de carga estacionária, mas não-uniforme dada por , onde é uma constante positiva e é o ângulo polar, medido a partir do eixo .
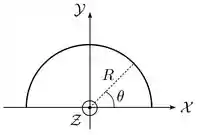
- Determine a carga total contida no semianel.
- Determine o vetor campo elétrico produzido pelo semianel em seu centro.
Questão 62
Considere uma barra retilínea, fina, disposta no eixo , entre as coordenadas e . Em tal barra, existe uma distribuição de carga, com densidade linear
sendo
Calcule a carga total da barra .
Determine o campo elétrico resultante (devido à barra) em um ponto do seu plano médio, a uma distância da barra.
Determine a expressão assintótica de tal campo, no limite em que . Interprete o seu resultado.
Ver solução completaQuestão 63
Considere um segmento retilíneo, de comprimento , disposto sobre o eixo como mostra a figura abaixo. Ele encontra-se carregado com um densidade linear de carga constante .
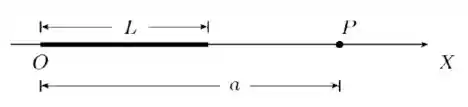
- Determine o campo elétrico (módulo, direção e sentido) em um ponto sobre o eixo , localizado a uma distância da extremidade do segmento que está sobre a origem .
- Uma partícula de carga é posicionada sobre o ponto . Determine a força elétrica (módulo, direção e sentido) que essa partícula exerce o segmento.
- Determine uma expressão assintótica para a força encontrada no item anterior no limite de . Interprete esse resultado.
Questão 64
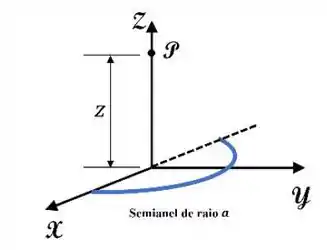
Um anel semicircular de raio está carregado negativamente com uma carga distribuída uniformemente ao longo do seu comprimento. Qual é o valor da componente do campo elétrico produzido pelo semianel em um ponto sobre o eixo , localizado a uma distância da origem?
Questão 65
Considere um bastão (muito fino) isolante de comprimento carregado com uma densidade de carga uniforme . O bastão está orientado na direção horizontal.
Desenhe o bastão e o sistema de coordenadas utilizado.
Calcule agora o campo elétrico (módulo, direção e sentido) nos seguintes pontos:
Em um ponto qualquer numa altura acima do bastão.
Em um ponto numa altura acima do centro do bastão.
Se agora o bastão tem comprimento infinito, como se modifica a resposta do item ?
Ver solução completaQuestão 66
Considere as seguintes afirmações:
- Campos eletrostáticos gerados por quaisquer distribuições de carga são campos conservativos;
- A força decorrente da indução de um momento de dipolo elétrico em materiais condutores é atrativa, enquanto em materiais isolantes é repulsiva;
- Apenas campos elétricos gerados por cargas puntiformes obedecem ao princípio de superposição.
Marque a opção que contém as afirmações CORRETAS:
(a) I;
(b) I e II;
(c) I e III;
(d) II e III.
(e) Todas as afirmações são corretas;
Ver solução completaQuestão 67
Um anel semicircular fino, isolante, de raio está posicionado sobre a porção superior do plano de um sistema de coordenadas e centrado na origem, como mostra a figura. Ele possui uma densidade linear de carga não uniforme dada por , sobre as componentes e do campo elétrico produzido pelo anel em seu centro, e , podemos afirmar que:
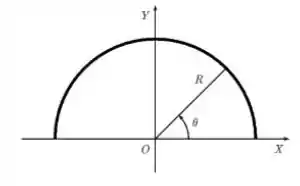
Questão 68
Um anel semicircular fino, isolante, de raio está posicionado sobre a porção superior do plano de um sistema de coordenadas e centrado na origem, como mostra a figura. Ele possui uma densidade linear de carga não uniforme dada por . Considere um elemento de carga da figura. Assinale a alternativa que representa a expressão da componente horizontal do campo elétrico infinitesinal produzido por este elemento de carga na origem.
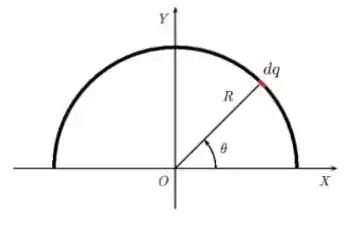
Questão 69
Dois pedaços de fios retos semi-infinitos, isolantes e carregados (densidades de carga λ e – λ) estão colados a dois semicírculos de raio R formados de fios isolantes carregados (densidades de carga 2λ e - λ), como mostra a Figura 1.
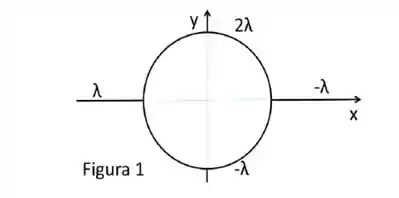
a) Calcule o vetor campo elétrico na origem das coordenadas devido aos fios semi-infinitos retos.
b) Calcule o vetor campo elétrico na origem das coordenadas devido aos fios semicirculares.
c) Calcule o campo eletrostático vetorial total na origem das coordenadas.
Ver solução completaQuestão 70
5ª questão - Uma carga de está distribuída uniformemente em um segmento do eixo que vai de a . Qual é a componente do campo elétrico no ponto sobre o eixo localizado em ?
A)
B)
C)
D)
E)
Ver solução completaQuestão 71
1 - Uma carga de está uniformemente distribuída ao longo do eixo x de a . Qual das seguintes integrais está correta para a magnitude (em N/C) do campo elétrico em m no eixo x?
Ver solução completaQuestão 72
11. (D) Uma casca isolante cilíndrica de raio e altura possui uma carga uniformemente distribuída sobre sua área.
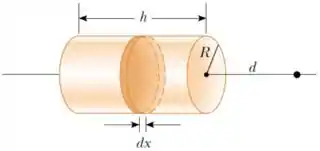
(b) Determine o vetor campo elétrico a uma distância do lado direito do cilindro, como indicado na figura. Sugestão: Divida o cilindro em anéis infinitesimais coaxiais como indicado na figura e use o resultado obtido em aula para o campo elétrico produzido por um anel uniformemente carregado. A integral resultante pode ser resolvida por substituição simples.
Ver solução completaQuestão 73
11. (D) Uma casca isolante cilíndrica de raio e altura possui uma carga uniformemente distribuída sobre sua área.
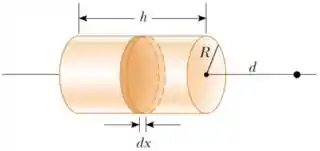
(c) Discuta o comportamento da expressão obtida no item anterior no limite .
Ver solução completaQuestão 74
. Considere uma barra fina, retilínea e isolante, de comprimento , disposta sobre o eixo de um sistema de coordenadas com uma de suas extremidades sobre a origem, como mostra a figura abaixo. Ela encontra-se carregada com uma densidade linear de carga estacionária, mas não-uniforme dada por , onde é uma constante positiva.
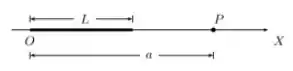
Determine a carga total da barra.
Determine o vetor campo elétrico em um ponto sobre o eixo , localizado a uma distância da extremidade da barra que está sobre a origem .
Ver solução completaQuestão 75
Uma barra isolante, de espessura desprezível e comprimento , repousa sobre o eixo desde até . Ela recebe uma carga total que se distribui de modo não uniforme de acordo com a densidade linear de carga dada pela função , onde é uma constante com dimensões apropriadas. O sistema de coordenadas está indicado na figura.

Calcule o valor da carga total na barra, , e a unidade SI (Sistema Internacional) da constante .
Calcule o valor (componente apenas) do vetor campo elétrico no ponto de coordenadas .
O campo elétrico produzido por toda a barra no ponto , de coordenadas , vale . Em que ponto do espaço se deveria colocar a carga pontual para que o campo total resultante fosse nulo em ?
Ver solução completaQuestão 76
Considere o bastão delgado da figura, de comprimento , posicionado ao longo do eixo . Sobre o bastão existe uma densidade linear de carga dada por , onde é uma constante positiva (todas as unidades estão no SI). Um determinado ponto possui coordenadas retangulares onde .
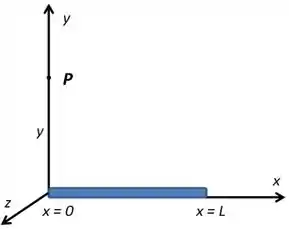
a) Considerando a referência dos potenciais no infinito encontre o potencial no ponto .
b) Suponha agora que o potencial gerado pelo bastão no ponto seja dado pela expressão:
onde é uma constante positiva (todas as unidades estão no SI). Calcule a componente do vetor campo elétrico em a partir da expressão fornecida. Responda também se as componentes e do vetor campo elétrico em , devidas ao bastão com a densidade linear de carga original, são positivas, negativas ou nulas, sem precisar calculá-las diretamente a partir da lei de Coulomb (Sugestão: use argumentos de simetria).
Considere novamente a expressão dada no item (b), agora com os valores numéricos , e em unidades do SI.
c) Calcule todos os pontos do espaço em que a carga puntiforme pode ser colocada de modo que o potencial TOTAL gerado em tenha o triplo do valor daquele gerado unicamente pelo bastão.
Ver solução completaQuestão 77
A figura abaixo representa uma esfera maciça não-condutora, de raio e densidade volumétrica de carga constante . Tal esfera maciça está envolvida por uma casca esférica concêntrica, também não-condutora, de raio interno e raio externo . A casca esférica tem uma carga elétrica uniformemente distribuída em toda sua extensão. A distância radial ilustrada na figura (segmento reto tracejado) pode variar no intervalo , onde localiza o centro comum da esfera maciça e da casca esférica. Além disso, uma carga pontual está fixada num ponto localizado entre a esfera maciça e a casca esférica, onde . Nestas circunstâncias, calcule:
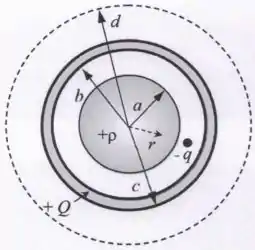
- O módulo do campo elétrico em um ponto no interior da esfera maciça, onde .
- O módulo da força elétrica total sentida pela carga que está na região onde .
- Para que valor da carga da casca o fluxo elétrico total através da superfície esférica tracejada de raio ilustrada na figura é nulo?
Questão 78
a) Uma haste infinita, isolante e de raio desprezível, possui uma densidade linear de carga . Calcule o vetor campo elétrico a uma distância radial r medida desde o eixo da haste.
Ver solução completaQuestão 79
O campo elétrico criado por uma barra fina de comprimento com carga num ponto do seu plano médio de simetria, a uma distância , é dado por:
Sabendo disso, qual é o campo elétrico resultante no centro de um quadrado de lado , que possui três arestas carregadas uniformemente com carga e a quarta com carga , confirme a figura abaixo?
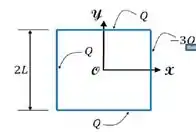
Escolha uma:
- O campo é nulo
Questão 80
Escolha uma:
- 0
Questão 81
Uma barra isolada, de comprimento , tem uma carga distribuída uniformemente ao longo de sua extensão, conforme a figura.

Determine o vetor campo elétrico no ponto , situado a uma distância da extremidade direita da barra;
Suponha que uma outra carga isolada puntiforme seja colocada num outro ponto distante da extremidade direita da barra. Determine o vetor campo elétrico no ponto devido apenas à carga isolada;
Determine, agora, o vetor campo elétrico total no ponto ;
Ver solução completaQuestão 82
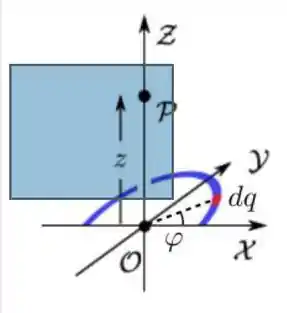
Um fio semicircular fino, de raio R, encontra-se no plano , com seu centro na origem de um sistema de coordenadas cartesianas e contido nos primeiro e segundo quadrantes, como mostrado na figura abaixo. Ele possui uma densidade linear de carga elétrica constante e positiva λ.
(a) Determine a carga total do fio.
(b) Qual(is) componente(s) do vetor campo elétrico resultante em um ponto qualquer do eixo Z é(são) nula(s)? Justifique.
(c) Deduza, em detalhe, uma expressão para o vetor campo elétrico resultante no ponto P acima mencionado.
Questão 83
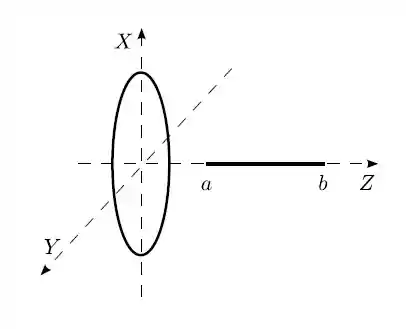
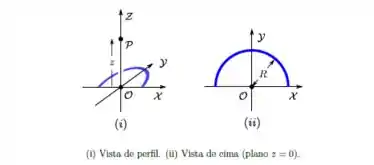
O campo elétrico sobre o eixo de simetria (eixo ) de um anel de raio e carga total é dado por
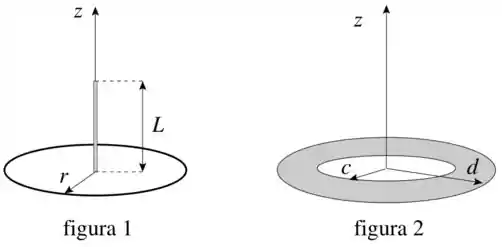
(a) Calcule a força elétrica que o anel exerce sobre um fio retilíneo de comprimento e densidade linear de carga , posicionado sobre o eixo , conforme a figura .
(b) Calcule o campo elétrico sobre o eixo de simetria (eixo ) de um disco vazado com raio interno e raio externo , carregado com uma densidade superficial de carga uniforme , conforme a figura 2.
Ver solução completaQuestão 84
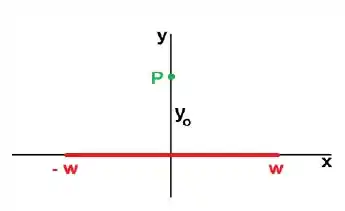
A fita cuja seção transversal está mostrada na Figura tem largura , espessura desprezível e comprimento infinito ao longo do eixo z. Está carregada com a densidade superficial de carga onde é constante e positiva .
- Inicialmente, determine uma expressão geral para o vetor campo elétrico devido a um fio infinito carregado com uma densidade linear de carga positiva (), observando seu módulo e sentido em cada ponto do espaço.
- Em seguida, considere que a fita pode ser decomposta em fios de espessuras infinitesimais. Finalmente, use o resultado do item anterior para determinar o vetor campo elétrico (módulo e sentido) devido à fita em um ponto de observação arbitrário do eixo situado acima dela e que dista da origem.
Questão 85
Considere um anel com raio e espessura desprezível que está parcialmente carregado. O centro do anel coincide com a origem do sistema de coordenadas, conforme mostrado na figura abaixo e encontra-se disposto com a origem ao longo do plano . A distribuição de carga no anel é dada por:

onde é o ângulo polar e é uma constante positiva. Considere nulo o potencial elétrico no infinito.
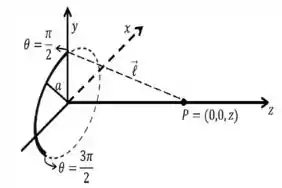
- Determine o vetor campo elétrico no ponto do eixo do anel.
- Determine o potencial elétrico no ponto do eixo do anel.