Distancia temporal entre dois eventos. Os eventos e ocorrem nas seguintes coordenadas espaçotemporais nos referenciais da Fig. 37-25: no referencia , e ; no referencial , e . No referencial , e . (a) Escreva uma expressão para em termos do parâmetro de velocidade e dos dados do problema. Faça um gráfico de em função de (b) para e (c) para . (d) Para que valor de o valor de é o mínimo? (e) Qual é o valor mínimo? (f) Um dos dois eventos pode ser a causa do outro? Justifique sua resposta.
Passo 1
Para resolvermos esse problema, vamos utilizar a Eq. 2’ da tabela 37-2, onde relacionamos o tempo que se passa no referencial com o tempo no referencial em função do fator . Vamos também plotar os gráficos após termos a equação de em função de e encontrar os valores mínimos da função.
Passo 2
- Vamos começar utilizando a equação mencionada no passo 1. Ela é da seguinte forma
- Para plotarmos o gráfico, vamos analisar a equação. Temos que para valores muito pequenos de , será aproximadamente 1. Dessa forma, temos que para o primeiro intervalo onde a equação ficará como de primeiro grau, da forma
- Para esse novo intervalo, temos que a equação será do tipo
- Para encontrarmos o valor de para qual é mínimo, temos que derivar a equação e igualar a 0. Derivando então, temos que
- Substituindo esse valor que encontramos na primeira equação que encontramos (já faz tantos passos...será que ainda me lembro?), temos que nosso valor mínimo para será
- Ufa! Finalmente o último passo. Foi muito bom sofrer com vocês até aqui. Como no referencial de qualquer um dos eventos, os acontecimentos não ocorrem simultaneamente, temos que é possível sim que um seja a causa do outro.
Substituindo os valores dados no problema, temos que , e
. Assim, a equação fica
Com variando com da seguinte forma
Passo 3
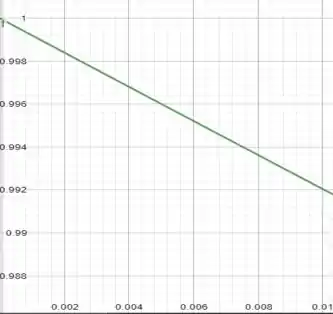
Passo 4
E para o intervalo dado, temos que a equação se comportará da seguinte forma

Passo 5
Usando a regra do produto para derivar essa equação maravilhosa, chegamos que
Temos que a única maneira dessa equação ser 0 é se
Passo 6
Passo 7
Resposta
d)
e)