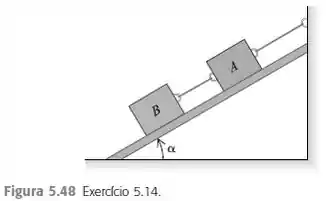
Dois blocos, cada um com peso , são mantidos em equilíbrio em um plano inclinado sem atrito (Figura ). Em termos de e do ângulo a do plano inclinado, determine a tensão:

a) na corda que conecta os dois blocos;

b) na corda que conecta o bloco com a parede.

c) Calcule o módulo da força que o plano inclinado exerce sobre cada bloco.

d) Interprete suas respostas para os casos e .

Então vamos começar esboçando o diagrama de corpo livre do nosso sistema:

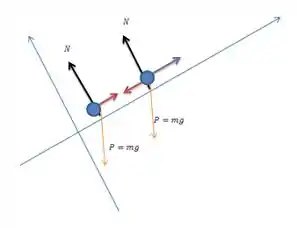
Para o bloco , mais a esquerda do desenho, na direção horizontal temos o equilíbrio da componente horizontal da força peso e a tensão no fio (vetor em vermelho) que liga os blocos. Assim temos:

Para o bloco , mais a direita, temos na direção horizontal a tensão do fio entre os blocos e a componente horizontal do peso, ambas forças apontando para a esquerda (sentido negativo) e a tensão que liga o bloco na parede apontando para a direita (sentido positivo).

Como o sistema está em equilíbrio, as forças para a direita são iguais as forças para esquerda e temos:

Mas do item anterior sabemos que , assim podemos determinar :

Isolando qualquer um dos blocos podemos determinar o valor de . Vou usar aqui o bloco .

Olhando para a direção vertical temos para cima a força normal e para baixo a componente vertical do peso .

Como o sistema está em equilíbrio essas duas forças devem ser iguais em módulo e teremos:

Para o valor do seno é zero e do cosseno é máximo. Isso quer dizer que as tensões no fio são nulas e a força normal fica sendo igual ao peso :

Faz sentido não é? O ângulo representa um plano reto, sem inclinação. Sendo assim não teremos mais o fio tensionado, pois não haverá nenhuma força puxando o sistema para baixo.

Mas a situação vai se invertendo à medida que for se aproximando de . Nesse caso vai crescendo e se aproximando de seu valor máximo, já o valor de vai diminuindo, chegando a zero. Assim as tensões e a normal mudam de valores, saca só:

Quando temos a tensão na parte superior (entre o bloco e a parede) deve ser suficientemente grande para equilibrar os dois blocos, ou seja, deve ter módulo igual à soma dos pesos dos dois blocos. Já a normal tem seu valor nulo, pois não há mais contato dos blocos com a superfície.

Valeu, galera! Até a próxima! 😉