Exercícios de Plano Inclinado - Lista de Exercícios Resolvida
Questão 1
Uma caixa está em repouso em um plano inclinado, sem deslizar, conforme a figura. Se aumentarmos continuamente o ângulo de inclinação do plano (medido a partir da horizontal), o módulo da força normal:
a) decresce de forma não linear.
b) não muda.
c) decresce linearmente.
d) aumenta de forma não linear.
e) aumenta linearmente.
Ver solução completaQuestão 2
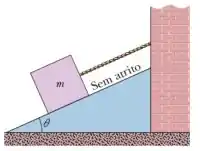
Um bloco de massa , está apoiado em um plano inclinado, que possui um ângulo com a horizontal. Sabendo que o bloco desliza sem atrito pelo plano inclinado, determine o módulo da aceleração do bloco e o valor da força normal que a superfície faz nele. Considere que o módulo da aceleração da gravidade é .
Questão 3
A Fig. 5-60 mostra parte de um teleférico. A massa máxima permitida de cada cabina com passageiros é de . As cabinas que estão penduradas em um cabo de sustentação, são puxadas por um segundo cabo ligado à torre de sustentação de cada cabina. Suponha que os cabos estão esticados e inclinados de um ângulo . Qual é a diferença entre as tensões de partes vizinhas do cabo que puxa as cabines se as cabinas estão com a máxima massa permitida e estão sendo aceleradas para cima a .

Questão 4
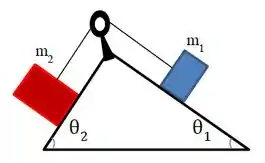
Dois blocos ligados entre si por uma corda estão pendurados em um plano inclinado, de acordo com a figura abaixo. Não há atrito entre os blocos e o plano inclinado.
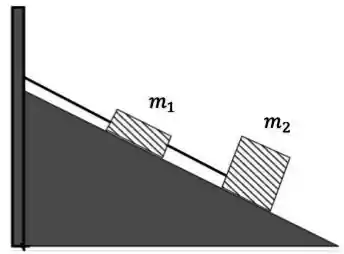
A tração medida na corda que liga o bloco de massa à parede é três vezes maior que a tração que liga o bloco ao bloco . É correto afirmar que a razão entre as massas vale:
Questão 5
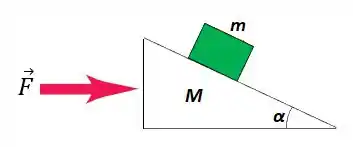
Na Fig. 5-41, um caixote de massa é empurrado por uma força horizontal que o faz subir uma rampa sem atrito () com velocidade constante. Quais são os módulos de e (b) da força que a rampa exerce sobre o caixote?
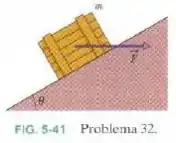
Questão 6
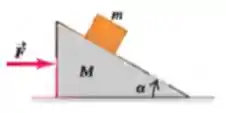
Um cunha de peso e ângulo está sobre uma superfície horizontal sem atrito. Um bloco de peso é posto sobre a cunha e uma força horizontal é aplicada na cunha (veja a figura). Também não há atrito entre o bloco e a cunha. Qual deve ser o módulo de se queremos que o bloco permaneça a uma altura constante acima da superfície horizontal?
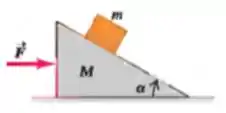
Questão 7
(Cap 11 – Ex 4) Uma esfera maciça e homogênea rola para baixo em um plano inclinado.
a) Qual deve ser o ângulo de inclinação do plano para que a aceleração linear do centro da esfera tenha um módulo de ?
b) Se um bloco sem atrito deslizasse para baixo no mesmo plano inclinado, o módulo da aceleração seria maior, menor ou igual a ? Por quê?
Ver solução completaQuestão 8
[4] A figura abaixo mostra uma caixa com massa que está apoiada sobre um plano inclinado que faz um ângulo com a horizontal. Esta caixa está amarrada, via uma corda sem massa e inextensível, a uma outra caixa de massa . A polia pela qual passa a corda é considerara como ideal. Os coeficientes de atrito estático e cinético entre e a superfície do plano inclinado são e , respectivamente.
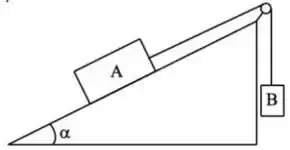
(a) Faça o diagrama de forças para cada uma das caixas, considerando que a caixa sobe o plano inclinado.
Ver solução completaQuestão 9
[4] A figura abaixo mostra uma caixa com massa que está apoiada sobre um plano inclinado que faz um ângulo com a horizontal. Esta caixa está amarrada, via uma corda sem massa e inextensível, a uma outra caixa de massa . A polia pela qual passa a corda é considerara como ideal. Os coeficientes de atrito estático e cinético entre e a superfície do plano inclinado são e , respectivamente.
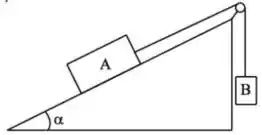
(b) Ache a expressão do módulo da aceleração da caixa em função dos parâmetros dados no enunciado.
Ver solução completaQuestão 10
[4] A figura abaixo mostra uma caixa com massa que está apoiada sobre um plano inclinado que faz um ângulo com a horizontal. Esta caixa está amarrada, via uma corda sem massa e inextensível, a uma outra caixa de massa . A polia pela qual passa a corda é considerara como ideal. Os coeficientes de atrito estático e cinético entre e a superfície do plano inclinado são e , respectivamente.
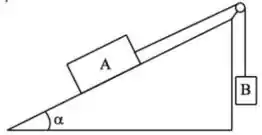
(c) ache a expressão do modulo da tensão na corda em função dos parâmetros dados no enunciado.
Ver solução completaQuestão 11
Dois blocos de massas e estão ligados por uma corda em um plano inclinado sem atrito que forma um ângulo de em relação a horizontal, conforme figura. Se a corda que liga os blocos se rompe, calcule o módulo da aceleração do bloco .
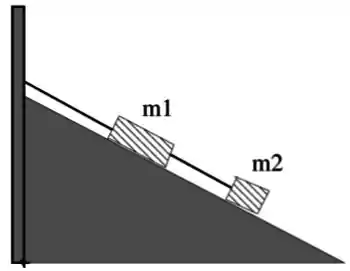
a)
b)
c)
d)
e) nenhuma das anteriores
Ver solução completaQuestão 12
Dois blocos ligados entre si por uma corda estão pendurados em um plano inclinado, de acordo com a figura abaixo. Não há atrito entre os blocos e o plano inclinado.
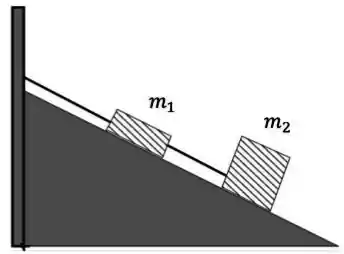
A tração medida na corda que liga o bloco de massa à parede é três vezes maior que a tração que liga o bloco ao bloco . É correto afirmar que a razão entre as massas vale:
Questão 13
Dois blocos ligados entre si por uma corda estão pendurados em um plano inclinado, de acordo com a figura abaixo. Não há atrito entre os blocos e o plano inclinado.
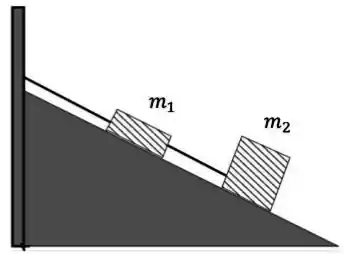
Para qual inclinação do plano em relação à horizontal a força de tração exercida no bloco 2 é igual à força normal exercida pelo plano neste bloco?
- 30°
- 45°
- 60°
Questão 14
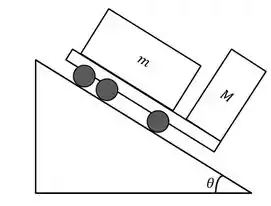
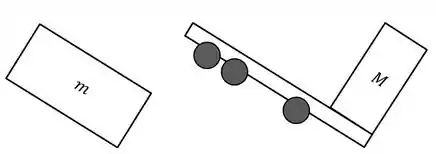
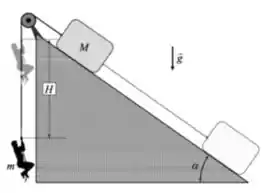
Um plano inclinado de massa M repousa em uma mesa horizontal sem atrito. Um bloco de massa m é colocado sobre esse plano (figura abaixo). Não existe atrito entre o bloco e o plano. O sistema é liberado do repouso.
(b) Sua resposta da parte (a) se aproxima do resultado correto quando é muito grande?
Ver solução completaQuestão 15
Parte I:
Uma caixa de massa está sobre um plano inclinado que faz um ângulo com a horizontal. Ela está ligada por uma corda de massa desprezível, que passa por uma roldana ideal, a uma outra caixa de massa , conforme a figura ao lado. Os planos inclinados fazem entre si e não possuem atrito.
(a ) Faça os diagramas de forças dos blocos 1 e 2.
(b) Determine o módulo da aceleração de cada bloco.
(c) Encontre o módulo da tensão 𝑇 na corda.
Ver solução completaQuestão 16
Um cunha de peso e ângulo está sobre uma superfície horizontal sem atrito. Um bloco de peso é posto sobre a cunha e uma força horizontal é aplicada na cunha (veja a figura). Também não há atrito entre o bloco e a cunha. Qual deve ser o módulo de se queremos que o bloco permaneça a uma altura constante acima da superfície horizontal?
Questão 20
Um bloco é lançado para cima sobre uma superfície lisa de um plano inclinado com uma velocidade inicial . O ângulo do plano inclinado em relação à horizontal é .
(a) Que distância sobre o plano o bloco consegue subir?
(b) Que tempo o bloco leva para atingir essa altura máxima?
(c) Qual é a velocidade do bloco ao chegar de volta ao ponto de lançamento?
Ver solução completaQuestão 21
No plano inclinado abaixo, qual a massa necessária para deixar o sistema em equilíbrio, na ausência de atrito?
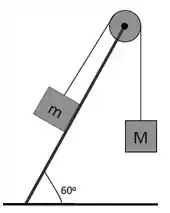
(a)
(b)
(c)
(d)
(e)
Dado: ;
Ver solução completaQuestão 22
Um bloco de madeira é arrastado por uma força sobre uma superfície metálica rugosa, conforme ilustrado nas figuras abaixo. No primeiro caso, o bloco é arrastado sobre uma superfície horizontal enquanto que, no segundo caso, é arrastado sobre um plano inclinado. A magnitude da força é idêntica em ambos os casos. Em relação à força normal exercida pela superfície sobre o bloco em cada caso, é correto afirmar que:
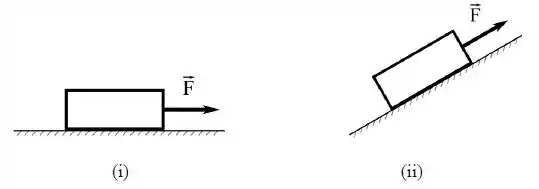
(a) A força normal é igual em ambos os casos.
(b) A força normal exercida em é maior que a exercida em .
(c) A força normal exercida em é menor que a exercida em .
(d) A força normal exercida em ambos os casos depende da magnitude de .
(e) Apenas a força normal no caso depende da magnitude de .
Ver solução completaQuestão 23
Qual é o módulo da força horizontal , mostrada na figura abaixo, para o qual o bloco de massa não escorrega para cima nem para baixo sobra a cunha, de massa ? Todas superfícies são livres de atrito.
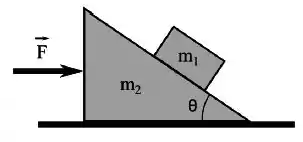
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 24
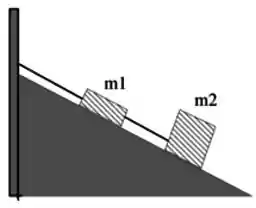
Dois blocos ligados entre si por uma corda estão pendurados em um plano inclinado, de acordo com a figura abaixo. Não há atrito entre os blocos e o plano inclinado. A tensão medida na corda que liga o bloco de massa à parede é três vezes maior que a tensão que liga o bloco ao bloco . É correto afirmar que a razão entre as massas vale:
a)
b)
c)
d)
e)
Questão 25
Uma caixa está em repouso em um plano inclinado, sem deslizar, conforme a figura. Se aumentarmos continuamente o ângulo de inclinação do plano (medido a partir da horizontal), o módulo da força normal:
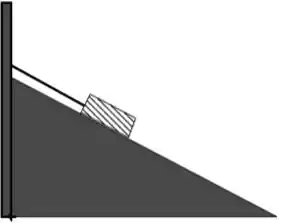
a) decresce de forma não linear.
b) não muda.
c) decresce linearmente.
d) aumenta de forma não linear.
e) aumenta linearmente.
Ver solução completaQuestão 26
Três blocos, A, B e C de mesma massa repousam sobre as faces de um sólido formado de superfícies planas, como indicado na figura abaixo, onde e , . Considerando o módulo das forças normais exercida pelas superfícies sobre os blocos é correto afirmar que:
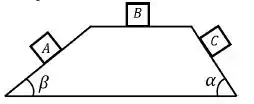
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 27
Um caminhão de massa desce uma ladeira que faz uma inclinação angular com a horizontal a uma velocidade constante . O caminhão carrega na carroceria uma caixa de massa . Ao avistar um obstáculo na pista, o motorista freia bruscamente, travando os pneus, e começa a derrapar. O coeficiente de atrito cinético entre as rodas do caminhão e o chão é , e o coeficiente estático entre a caixa e o caminhão é tal que o objeto não desliza.
(a) Desenhe na figura todas as forças exercidas no caminhão e na caixa.
(b) Quais são os pares de força de ação e reação?
(c) Calcule a força de atrito exercida no caminhão e na caixa como função das variáveis do problema.
(d) Qual o limite das forças de atrito para e
(e) Substituindo os valores de , e encontre a distância percorrida até o caminhão parar. Utilize e aproximação e .
(f) O que você deverá mudar em seus cálculos se o caminhão estiver subindo a ladeira em vez de descendo? Recalcule o resultado do ítem anterior para este caso.
Ver solução completaQuestão 28
No diagrama abaixo, um bloco é mantido em repouso em um plano inclinado graças à força horizontal
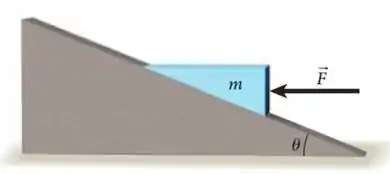
Desprezando qualquer força de atrito, quanto vale a força ?
a.
b.
c.
d.
e.
Ver solução completaQuestão 29
Dois blocos de massa e estão ligados por um fio ideal como ilustrado na figura abaixo.
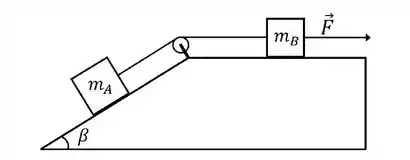
O bloco de massa desliza sobre a parte inclinada de um ângulo em relação à horizontal. Já o bloco de massa desliza sobre uma superfície plana. Sobre o bloco atua uma força de módulo paralela à horizontal. O coeficiente de atrito cinético entre os blocos e a superfície é igual .
Considerando que devido à ação da força o sistema passa a se mover para a direita:
a) Desenhe o diagrama de forças para cada um dos blocos.
b) Determine a aceleração do conjunto.
c) Determine a tensão no fio que une os blocos.
Suas respostas devem ser dadas em termos de ,, , , e .
Ver solução completaQuestão 30
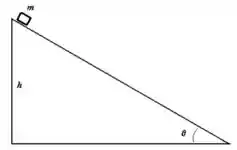
7. Um bloco de massa é colocado no topo de uma rampa de altura que faz um ângulo com a horizontal (acima à direita). Supondo que o bloco vai deslizar, e que o coeficiente de atrito cinético vale , responda os itens abaixo:
b) Calcule as forças que atuam no bloco.
Questão 31
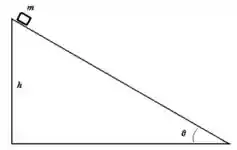
7. Um bloco de massa é colocado no topo de uma rampa de altura que faz um ângulo com a horizontal (acima à direita). Supondo que o bloco vai deslizar, e que o coeficiente de atrito cinético vale , responda os itens abaixo:
c) Calcule a aceleração do bloco.
Questão 32
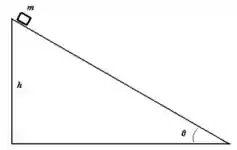
7. Um bloco de massa é colocado no topo de uma rampa de altura que faz um ângulo com a horizontal (acima à direita). Supondo que o bloco vai deslizar, e que o coeficiente de atrito cinético vale , responda os itens abaixo:
e) Calcule a energia mecânica do bloco no fim da rampa.
Questão 33
Um plano inclinado de massa M repousa em uma mesa horizontal sem atrito. Um bloco de massa m é colocado sobre esse plano (figura abaixo). Não existe atrito entre o bloco e o plano. O sistema é liberado do repouso.
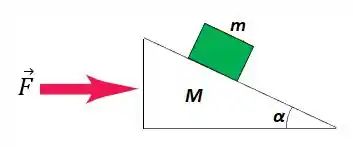
(a) Calcule a aceleração do plano e as componentes horizontal e vertical de aceleração do bloco.
Ver solução completaQuestão 34
Um plano inclinado de massa M repousa em uma mesa horizontal sem atrito. Um bloco de massa m é colocado sobre esse plano (figura abaixo). Não existe atrito entre o bloco e o plano. O sistema é liberado do repouso.
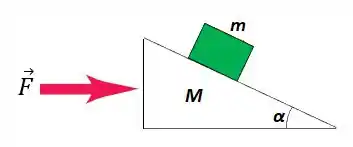
(c) Do ponto de vista de um observador estacionário, qual a forma da trajetória do bloco?
Ver solução completaQuestão 35
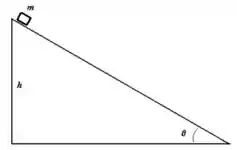
7. Um bloco de massa é colocado no topo de uma rampa de altura que faz um ângulo com a horizontal (acima à direita). Supondo que o bloco vai deslizar, e que o coeficiente de atrito cinético vale , responda os itens abaixo:
a) Escolha um referencial e desenhe um diagrama das forças que atuam sobre o bloco.
Questão 36
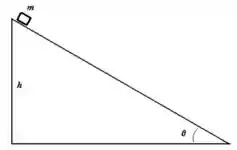
7. Um bloco de massa é colocado no topo de uma rampa de altura que faz um ângulo com a horizontal (acima à direita). Supondo que o bloco vai deslizar, e que o coeficiente de atrito cinético vale , responda os itens abaixo:
d) Calcule o trabalho de cada uma das forças que atua sobre o bloco do início ao fim da rampa.
Questão 37
Uma pedra esférica de raio , uniforme e maciça e parte do repouso e rola para baixo de uma colina de 30,0 m de altura e inclinação de , como indica a figura 3. A metade superior da colina é áspera o suficiente para fazer a pedra rolar sem deslizar, mas a metade inferior está coberta de gelo e não há atrito.
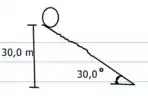
a) Calcule a aceleração da pedra na parte áspera.
b) Calcule a velocidade escalar de translação da pedra quando ela atinge a metade da colina.
c) Calcule a velocidade escalar de translação da pedra quando ela atinge a base da colina.
Ver solução completaQuestão 38
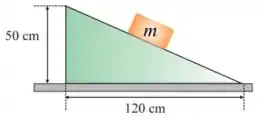
36. Um bloco de está parado sobre um plano inclinado, devido ao atrito. Qual a componente da força que aplica no plano inclinado:
(b) Qual o módulo, direção e sentido da força que o plano inclinado aplica em ?
Questão 39
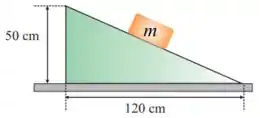
36. Um bloco de está parado sobre um plano inclinado, devido ao atrito. Qual a componente da força que aplica no plano inclinado:
(a) Perpendicular à superfície e tangente à superfície?
Questão 40
37. Um corpo de massa está apoiado em um plano liso de inclinação , o qual tem uma aceleração que mantém o corpo estacionário em relação ao plano, como mostra a figura 2.10. Determinar esta aceleração. O que acontecerá se o plano tiver uma aceleração com módulo maior que o valor encontrado?

Questão 41
Um corpo de massa é visto descendo um plano com velocidade constante; só há o plano e o corpo. Sabendo-se que o ângulo de inclinação do plano em relação à horizontal é igual a , pode-se afirmar que a resultante das forças que o plano inclinado exerce sobre o corpo tem módulo igual a
Questão 42
Nas academias de ginástica, usa-se um aparelho chamado pressão com pernas (leg press), que tem a função de fortalecer a musculatura das pernas. Este aparelho possui uma parte móvel que desliza sobre um plano inclinado, fazendo um ângulo de com a horizontal. Uma pessoa, usando o aparelho, empurra a parte móvel de massa igual a , e a faz mover ao longo do plano, com velocidade constante, como é mostrado na figura.
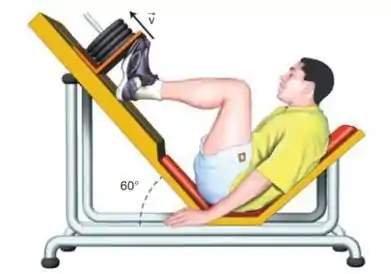
Considere o coeficiente de atrito dinâmico entre o plano inclinado e a parte móvel e a aceleração gravitacional .
Determine a intensidade da força que a pessoa está aplicando sobre a parte móvel do aparelho.
A)
B)
C)
D)
E)
Ver solução completaQuestão 43
(Capítulo 5.9 – Exercício 32) Na Fig. 5-40, um caixote de massa é empurrado por uma força horizontal que o faz subir uma rampa sem atrito com velocidade constante. Quais são os módulos (a) de e (b) da força que a rampa exerce sobre o caixote?
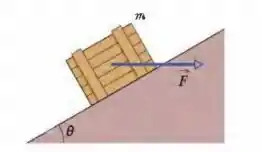
Questão 44
Um bloco desliza, para baixo, sobre um plano de inclinação , com velocidade constante. Ao atingir o final do plano, ele é projetado plano acima, por um dispositivo, com velocidade inicial . A aceleração da gravidade é .
Que distância acima, no plano, ele percorrerá, antes de parar?
Ver solução completaQuestão 45
Um bloco desliza, para baixo, sobre um plano de inclinação , com velocidade constante. Ao atingir o final do plano, ele é projetado plano acima, por um dispositivo, com velocidade inicial . A aceleração da gravidade é .
Ele tornará a deslizar para baixo no plano inclinado? Explique.
Ver solução completaQuestão 46
(Capítulo 5.9 – Exercício 19) Na Fig. 5-36, a massa do bloco é e o ângulo é Determine (a) a tensão na corda e (b) a força normal que age sobre o bloco. (c) Determine o módulo da aceleração do bloco se a corda for cortada.
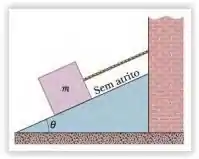
Questão 47
9) Um bloco inicialmente em repouso começa a deslizar do topo de um plano inclinado sem atrito (vide figura). O ângulo do plano inclinado é e sua base tem comprimento d. Se é o tempo que o bloca gasta para chegar à base do plano inclinado, é correto afirmar que:
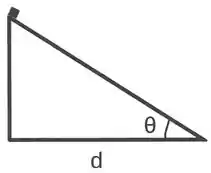
a)
b)
c)
d)
e)
Ver solução completaQuestão 48
(Capítulo 5.9 – Exercício 66) A Fig. 5-56 mostra uma caixa de massa sobre um plano inclinado sem atrito de ângulo . Ela está ligada por uma corda de massa desprezível a uma caixa de massa sobre uma superfície horizontal sem atrito. A polia não tem atrito e sua massa é desprezível. (a) Se o módulo da força horizontal é , qual é a tensão da corda? (b) Qual é o maior valor que o módulo de pode ter sem que a corda fique frouxa?
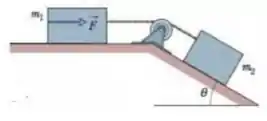
Questão 49
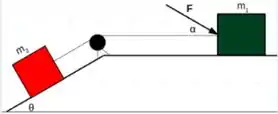
. Na figura, o bloco tem peso e bloco tem peso e está sobre uma rampa que faz com a horizontal. Uma força com módulo é aplicada sobre o bloco fazendo um ângulo de com a horizontal. Considere que não existe atrito entre os blocos e as superfícies e que a corda e a polia são ideias. Determine a aceleração dos blocos e determine se o bloco está subindo ou descendo a rampa. Considere .
Questão 50
9) Um alpinista de massa que visa agilizar a sua subida por uma parede vertical de uma encosta triangular se utiliza da liberação e deslizamento de uma caixa de equipamentos de massa pelo lado inclinado em da encosta e uma corda de massa desprezível. Ele se dependura na extremidade livre da corda cuja outra extremidade está amarrada à caixa e se solta. Sabe-se que o coeficiente de atrito cinético entre a caixa e a superfície da encosta é e a presença de uma polia no alto da encosta permite a livre movimentação da corda.
- Faça um diagrama mostrando todas as forças que atuam tanto na caixa quanto no alpinista quando eles estiverem em movimento.
- Escreva a segunda lei de Newton para a caixa e para o alpinista.
- Obtenha os módulos das acelerações e da caixa e do alpinista respectivamente bem como os módulos das forças de tensão e na corda em cada um dos lados da encosta.
- Determine o intervalo de tempo que levará para que o alpinista suba uma altura supondo que ele pariu do repouso e que , e
Dados: e .
Ver solução completaQuestão 51
Um vagão de massa está sobre um plano inclinado de inclinação , ligado a uma esfera suspensa, de massa , pelo sistema de cabos e polias ideais, como ilustrado na figura O coeficiente de atrito cinético entre o vagão e o plano inclinado é e o sistema é solto do repouso.
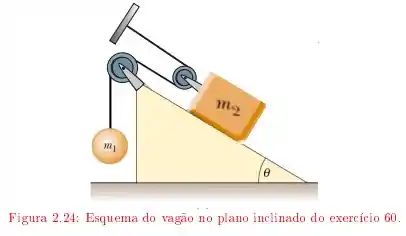
a) Determinar as relações entre os deslocamentos e as velocidades das massas e ;
Ver solução completaQuestão 52
Um vagão de massa está sobre um plano inclinado de inclinação , ligado a uma esfera suspensa, de massa , pelo sistema de cabos e polias ideais, como ilustrado na figura O coeficiente de atrito cinético entre o vagão e o plano inclinado é e o sistema é solto do repouso.
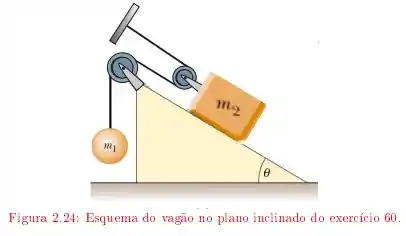
b) Utilizando a conservação da energia, calcule de que distância o vagão terá se deslocado, ao longo do plano inclinado, quando sua velocidade atingir
Ver solução completaQuestão 53
Um bloco de massa é solto em repouso em um plano inclinado de em relação ao plano horizontal, com coeficiente de atrito cinético Depois de percorrer uma distância ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava relaxada, de acordo com o esquema mostrado na figura .

a) Qual é a compressão sofrida pela mola?
Ver solução completaQuestão 54
Um bloco de massa é solto em repouso em um plano inclinado de em relação ao plano horizontal, com coeficiente de atrito cinético Depois de percorrer uma distância ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava relaxada, de acordo com o esquema mostrado na figura .

c) Se o coeficiente de atrito estático com o plano é de , que acontece com o bloco logo após colidir com a mola?
Ver solução completaQuestão 55
Um bloco de massa é solto em repouso em um plano inclinado de em relação ao plano horizontal, com coeficiente de atrito cinético Depois de percorrer uma distância ao longo do plano inclinado, o bloco colide com uma mola de constante , de massa desprezível, que se encontrava relaxada, de acordo com o esquema mostrado na figura .

b) Qual é a energia dissipada pelo atrito durante o trajeto do bloco desde o alto do plano até a compressão máxima da mola? Que fração representa da variação total de energia potencial durante o trajeto?
Ver solução completaQuestão 56
Q - A figura mostra um bloco de massa em repouso sobre um plano inclinado com inclinação . Ele está ligado a outro bloco, de massa , suspenso por meio de uma corda sem massa que passa por uma polia também desprovida de massa e livre de atrito. Os coeficientes de atrito estático e cinético com a superfície são, respectivamente, e . Qual é o valor da massa , em kilogramas, para que o bloco de massa suba o plano inclinado com velocidade constante?
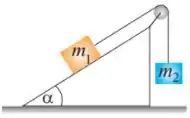
Questão 57
Um bloco de massa está sobre um plano inclinado de um ângulo com a horizontal. O coeficiente de atrito cinético entre o bloco e o plano é . O bloco está amarrado a um segundo bloco de massa que pende livremente de um cordão que passa por uma polia sem massa e sem atrito. Depois que o segundo bloco caiu , qual sua velocidade?

Questão 58
Um bloco de está sobre uma cunha sem atrito que tem uma inclinação de e uma aceleração para a direita, de tal forma que a massa permanece estacionária em relação a cunha (cf. figura).
(a) Desenhe o diagrama de corpo livre do bloco e use-o para determinar a magnitude da aceleração.

Questão 59
Um bloco de está sobre uma cunha sem atrito que tem uma inclinação de e uma aceleração para a direita, de tal forma que a massa permanece estacionária em relação a cunha (cf. figura).
(b) O que aconteceria se a cunha recebesse uma aceleração maior que esse valor? Justifique!

Questão 60
Um bloco de está sobre uma cunha sem atrito que tem uma inclinação de e uma aceleração para a direita, de tal forma que a massa permanece estacionária em relação a cunha (cf. figura).
(c) O que aconteceria se a cunha recebesse uma aceleração menor que esse valor? Justifique!

Questão 61
Considere e e o coeficiente de atrito cinético entre o plano e o bloco de é . Encontre a magnitude da aceleração das massas e a tensão na corda.

Questão 62
Um bloco de massa m escorrega sobre um piso sem atrito e depois sobre uma rampa sem atrito (Figura 4). O ângulo da rampa é 𝜃 e a velocidade do bloco antes de começar a subir a rampa é 𝑣0. O bloco escorregará até uma altura máxima h acima do piso, antes de parar. Mostre que h é independente de m e 𝜃, deduzindo uma expressão para h em termos de 𝑣0 e g.
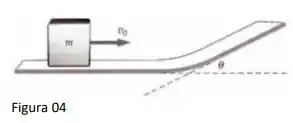
Questão 63
Um carro está dando voltas com velocidade de módulo constante numa estrada curva e inclinada de um ângulo em relação à horizontal. A massa do carro é e o raio da curva é . A velocidade do carro é tal que a força de atrito está atuando no sentido de impedir a derrapagem para cima na estrada. O coeficiente de atrito estático entre os pneus e a estrada de concreto é e o coeficiente de atrito cinético é .
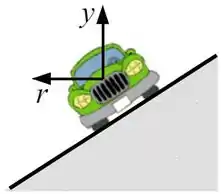
a) Faça o diagrama de corpo livre para o carro nesta situação.
b) Escreva a segunda lei de Newton correspondente na forma vetorial e por componentes nas direções indicadas na figura.
c) Se o ângulo de inclinação da curva com a horizontal for de e se a velocidade do carro for , calcule o valor do módulo da força de atrito estático. Nesta estrada, limite de velocidade é de .
Ver solução completaQuestão 64
Q - A figura mostra um bloco de massa em repouso sobre um plano inclinado com inclinação . Ele está ligado a outro bloco, de massa , suspenso por meio de uma corda sem massa que passa por uma polia também desprovida de massa e livre de atrito. Os coeficientes de atrito estático e cinético com a superfície são respectivamente, e . Qual é o valor da massa , em kilogramas, para que o bloco de massa desça o plano inclinado com velocidade constante?
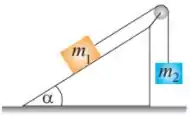
Questão 65
Um pequeno bloco de massa desliza sobre um plano de inclinação com a horizontal, sem atrito. Sobre ele atuam: a força normal exercida pelo plano e o peso . A opção correta abaixo é:
- O módulo da aceleração do bloco é igual a g.
- O módulo da força resultante sobre o bloco é:
- O módulo da força normal é:
- A aceleração do bloco tem sempre o mesmo sentido da velocidade, independente de qual seja a sua velocidade inicial.
Questão 66
Uma caixa de 20 kg está sobre uma rampa sem atrito inclinada de 15°. Alguém puxa a caixa rampa acima (Figura 3). Se a corda forma um ângulo de 40º com a horizontal, qual é a menor força F capaz de deslocar a caixa rampa acima?

Questão 67
Uma caixa está em repouso no alto de uma rampa inclinada de altura H. No final da rampa é posicionado um arco de circunferência de raio R, como ilustrado na figura abaixo. Em termos do raio R, qual a menor altura H para que a caixa atinja o ponto mais alto da circunferência (ponto A)? Desconsidere qualquer tipo de atrito
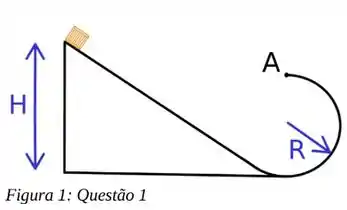
Questão 68
Uma bola homogênea (esfera) de raio , rola sem escorregar por um tobogã com um único de raio , como mostra a figura. A bola parte do repouso, com seu centro de massa na altura acima da base. Qual é o valor mínimo de para que a bola passe ponto no topo da volta fechada? Dê sua resposta em unidades do Sistema Internacional (SI).
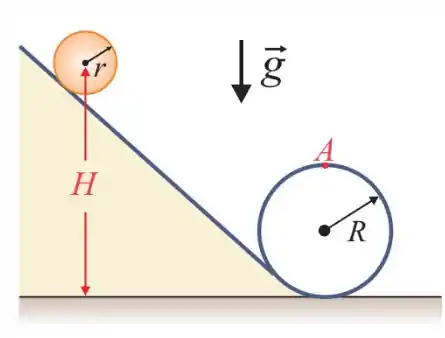
O momento de inércia de uma esfera de massa e raio em relação ao eixo de rotação que passa pelo seu centro de massa e é perpendicular ao plano da página é
a)
b)
c)
d)
e)
Ver solução completaQuestão 69
Um bloco começa a subir um plano inclinado sem atrito com velocidade inicial . O ângulo do plano inclinado é
Que distância ao longo do plano inclinado o bloco consegue atingir?
Ver solução completaQuestão 70
Um caixote de massa é empurrado por uma força horizontal que o faz subir uma rampa sem atrito com velocidade constante.
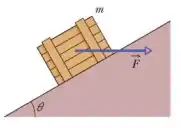
Qual é o módulo de ?
Ver solução completaQuestão 71
Um caixote de massa é empurrado por uma força horizontal que o faz subir uma rampa sem atrito com velocidade constante.
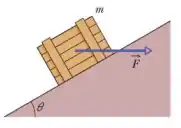
Qual é o módulo da força que a rampa exerce sobre o caixote?
Ver solução completaQuestão 72
Na figura a massa do bloco é e o ângulo é . Determine:
a aceleração do bloco se a corda for cortada;
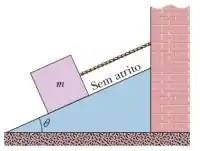
Questão 73
Um bloco começa a subir um plano inclinado sem atrito com velocidade inicial . O ângulo do plano inclinado é
Qual é a velocidade do bloco ao chegar de novo ao ponto de partida?
Ver solução completa