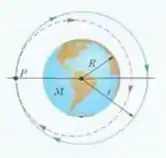
Duas pequenas espaçonaves, ambas de massa , estão na órbita circular em torno da Terra da figura, a uma altitude de . Kirk, o comandante de uma das naves, chega a qualquer ponto fixo da órbita antes e Picard, o comandante da segunda nave. Determine (a) o período e (b) a velocidade das naves. No ponto da figura, Picard dispara um retrofoguete instantâneo na direção tangencial à órbita, reduzindo a velocidade da nave em . Depois do disparo, a nave assume a órbita elíptica representada na figura por uma linha tracejada. Determine (c) a energia cinética e (d) a energia potencial da nave imediatamente após o disparo. Na nova órbita elíptica de Picard, quais são (e) a energia total , (f) o semieixo maior e (g) o período orbital ? (h) Quanto tempo Picard chega ao ponto antes de Kirk?

Belejóia, agora para a letra (b), queremos a velocidade orbital. Vamos lembrar da fórmula para a velocidade de uma órbita circular:

Sendo assim, substituindo os valores que conhecemos, obtemos que:

Agora vamos para a letra (c). O enunciado diz que Picard disparou um “retrofoguete” que fez a órbita perder da velocidade, e pede para calcularmos a nova energia cinética.

Mas pera lá meu patrão, vamos lembrar a fórmula da energia cinética dada como:

Como acabamos de calcular a velocidade inicial da órbita , a nova velocidade vai ser expressa por:

Logo:

Como já temos a massa, é só substituir:

Pronto, essa é a resposta da letra (c).

A letra (d) pede a nova energia potencial da nave imediatamente após o disparo. Esse último detalhe é muito importante, porque imediatamente após o disparo a energia potencial não muda.

A redução de velocidade afeta apenas a energia cinética de imediato. Mais tarde, essa perda de energia cinética vai obrigar a nave a fazer uma órbita mais baixa, e só aí podemos falar em uma redução de energia potencial.

Então a energia potencial fica:

A letra (e) quer a energia total na nave de Picard após o disparo.

Lembre-se que a energia total é a soma da potencial com a cinética, ou seja:

Então é só somar as respostas dos dois últimos itens.

Obs.: A energia total de um sistema fechado se conserva. Ou seja, em qualquer momento após o disparo, a energia total é a mesma, por isso não tem problema usarmos a energia potencial que foi calculada para o momento “imediatamente após” o disparo.

A letra (f) quer o período orbital da nova órbita. Mas vamos com cuidado, dá pra complicar essa questão muito rápido, mas na verdade podemos responder isso usando só a energia total que acabamos de calcular.

Lembre da fórmula para a energia total de uma órbita:

Esse é semi-eixo maior da órbita, que é simplesmente o raio no caso de uma órbita circular. Na figura dá pra ver que a órbita fica um pouco mais excêntrica após o disparo, então vamos usar o para sermos mais corretos.

Arrumando essa fórmula para isolar o :

Substituindo:

Para a letra (g), queremos o novo período orbital . Bom, agora que já temos o semi-eixo maior é tranquilo. Só precisamos usar a 3ª lei de Kepler:

Ou em minutos:

Veja que foi só repetir o procedimento que já tínhamos feito antes para a primeira órbita.

Antes de Picard disparar o míssil, o enunciado dizia que Kirk estava na sua frente. Nesse momento, o período orbital dos dois era:

Depois que Picard atirou, o período de Kirk continuou o mesmo, e o de Picard virou:

Ou seja, Picard ganhou uma vantagem de:

Como ele tinha um atraso de antes do disparo, no final das contas ele acabou com uma vantagem de:

Essa é a vantagem com que Picard chegar antes de Kirk em qualquer ponto da órbita, e portanto é a reposta da letra (h).