Enunciado
Física - Moysés - Vol. 4 - Ed: 1º - Capítulo 2.Problemas - Ex. 27
Uma esfera transparente de índice de refração , espelhada numa calota da sua superfície, com centro em (fig.), é usada como retro-refletor: qualquer raio 1 paralelo ao eixo e paraxial (próximo ao eixo) é refletido em e volta em sentido inverso (raio 2, fig.). Calcule o índice .
Passo 1
O primeiro passo é fazer um desenho esquemático desenhando os ângulos:
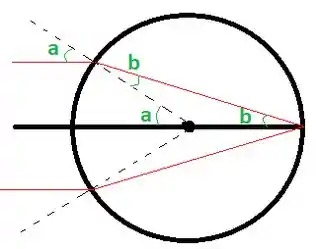
Note que temos um triângulo isósceles la dentro, por isso pude marcar dois ângulos . Além disso, note que
Logo,
Passo 2
Agora basta aplicar a lei de Snell:
Como , segue que
Mas sabemos que . Logo,
Passo 3
Como
temos que
Por fim, fazemos a aproximação paraxial:
Assim,
Resposta
Exercícios de Livros Relacionados
Um tanque cilíndrico horizontal com 2.20m de diâmetro contém água até a metade. O espaço acima da água é preenchido com um gás pressurizado de indice de refração desconhecido. Um pequeno laser pode se
Um raio de luz deslocando-se em um meio com velocidade v 1 parte de um ponto A e atinge um ponto B de outro meio com velocidade v 2 (Figura 33.55). O raio atinge a superficie a uma distância horizonta
Quando o Sol nasce ou se põe, ele parece estar no horizonte, porém, na realidade ele está abaixo do horizonte. A explicação para esse aparente paradoxo é que a luz se encurva ligeiramente quando penet
Um feixe de luz se deslocando de cima para baixo incide sobre uma película horizontal de espessura t , como mostra a Figura 33.57. O raio incidente divide-se em dois raios, A e B. O raio A é refletido
Um raio de luz propagando-se no ar incide com um ângulo θ a sobre a superfície superior de uma placa transparente (Figura 33.56), sendo suas duas superfícies planas e paralelas. a) Mostre que θ a = θ