Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.Problemas Adicionais - Ex. 69

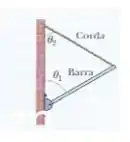
Na Fig. 12-74, uma viga homogênea de massa m está presa a uma parede por uma dobradiça na extremidade inferior, enquanto a extremidade superior e sustentada por uma corda presa na parede. Se θ 1 = 60 º , que valor deve ter o ângulo θ 2 para que a tensão da corda seja m g / 2 ?

Passo 1

Como o sistema está em equilíbrio o somatório dos momentos deve ser zero. As forças que agem sobre a viga são a reação no ponto de articulação, a força peso P e a tensão da corda T . O somatório dos momentos dessas três forças deve ser nulo. Vamos então calcular os momentos

Passo 2

Pra facilitar nossa vida, vamos calcular os momentos em torno da articulação.

- m g s i n θ 1 L 2 + T L c o s ϕ = 0

onde ϕ = θ 1 + θ 2 - 90 º . A figura abaixo ilustra um esqueminha do diagrama de forças.

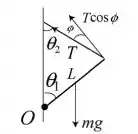
Resolvendo a equação para T , obtemos

T = m g 2 s i n θ 1 c o s θ 1 - θ 2 - 90 º = m g 2 s i n θ 1 s i n θ 1 + θ 2

Logo, é necessário que s i n θ 1 = s i n θ 1 + θ 2 . Uma solução é com θ 2 = 0 º , mas essa seria uma solução trivial, aí não vale. A outra seria com θ 2 = 60 º , que é a solução do problema.

Resposta

θ 2 = 60 º

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para quebrar a casca de uma noz com um quebra nozes, forças de pelo menos 40 N de módulo devem agir sobre a casca em ambos os lados. Para o quebra-nozes da figura abaixo, com distânciaL = 12 c m e d =
A figura da esquerda mostra uma rampa homogênea entre dois edifícios que leva em conta a possibilidade de que os edifícios oscilem ao serem submetidos a ventos fortes. Na extremidade esquerda, está pr
Na figura de cima uma viga homogênea de 40,0k g repousa simetricamente em dois rolamentos. As distâncias entre as marcas verticais ao longo da viga são iguais. Duas das marcas coincidem com a posição
Na Fig. 12-71, uma viga homogênea com 60 N de peso e 3,2 m de comprimento está presa a uma dobradiça na extremidade inferior e uma força horizontal F → de módulo 50 N age sobre a extremidade superior.
Uma viga homogênea tem 5,0 m de comprimento e uma massa de 53 kg. Na Fig. 12-72, a viga está sustentada na posição horizontal por uma dobradiça e um cabo; θ=60º. Em termos dos vetores unitários, qual