Enunciado

Física - Fundamentos de Física Volume 2 - Gravitação, Ondas e Termodinâmica - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 12.Problemas Adicionais - Ex. 56

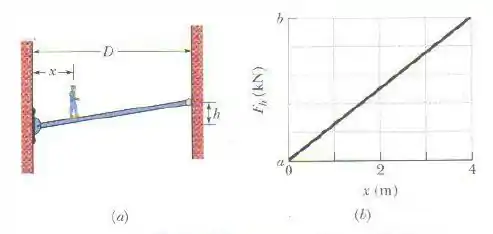
A figura da esquerda mostra uma rampa homogênea entre dois edifícios que leva em conta a possibilidade de que os edifícios oscilem ao serem submetidos a ventos fortes. Na extremidade esquerda, está presa por uma dobradiça na parede de um dos edifícios; na extremidade direita, tem um rolamento que permite o movimento ao longo da parede do outro edifício. A força que o edifício exerce sobre o rolamento não possui componente vertical, mas apenas uma força horizontal de módulo . A distância horizontal entre os edifícios é . O desnível entre as extremidades da rampa é . Um homem caminha ao longo da rampa a partir da extremidade esquerda. A figura da direita mostra em função da distância horizontal entre o homem e o edifício da esquerda. A escala do eixo de é definida por e . Quais são as massas (a) da rampa e (b) do homem?

Passo 1

Primeiro vamos entender bem aquele gráfico da esquerda. é a força que o edifício exerce sobre o rolamento que fica na extremidade direita da rampa, o enunciado garante que essa força não tem nenhum componente vertical (ou seja, toda a força é feita na direção perpendicular à parede).

Vamos usar o equilíbrio dos torques:

Primeiro precisamos escolher um ponto de referência. Se usarmos a dobradiça na ponta direita da rampa, vamos aproveitar todas as distâncias que o enunciado dá, e não anulamos nenhuma das forças que queremos calcular. Então vamos lá.

Passo 2

O peso da rampa age sobre o centro de massa dela, na metade do seu comprimento. Como ele empurra a rotação no sentido horário, vamos colocar um sinal negativo. Então o torque vai ser:

O peso do homem age no centro de massa do homem que é sempre dado pelo valor de , também a favor do sentido horário:

Nesses dois casos, como a força é vertical pra baixo e a rampa está praticamente paralela ao chão, aproximamos , por isso não apareceu nenhum seno nas fórmulas do torque.

E por último vamos ter o torque da força , que é a favor do sentido anti-horário. Dessa vez, a força é horizontal, então temos que incluir o seno do ângulo que a força faz com a rampa.