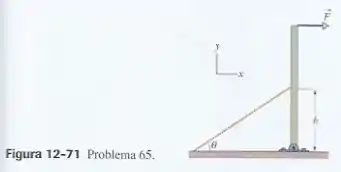
Na Fig. 12-71, uma viga homogênea com 60 N de peso e 3,2 m de comprimento está presa a uma dobradiça na extremidade inferior e uma força horizontal de módulo 50 N age sobre a extremidade superior. A viga é mantida na posição vertical por um cabo que faz um ângulo
ө=25º com o chão e está preso à viga a uma distância h=2,0 m do chão. Quais são (a) a tensão do cabo e (b) a força exercida pela dobradiça sobre a viga, em termos dos vetores unitários.
Passo 1
Bom, como o sistema está em equilíbrio, o somatório de todas as forças e torques gerados que agem sobre a barra é nulo. A forças que agem sobre a barra são: a força peso, a força oriunda de , a força de tensão do cabo e a força da dobradiça . Queremos achar os valores de e e , que são as componentes horizontal e vertical da reação da dobradiça.
Passo 2
Bom, a primeira coisa a que a gente pode fazer é escolher um ponto e calcular os momentos das forças com relação a esse ponto. Vamos escolher a dobradiça como ponto. Assim, o somatório dos momentos fica
Logo,
(a)
Passo 3
O próxímo passo é encontrar o valor do módulo da reação da dobradiça. Fazendo agora o somatório das forças na direção horizontal e vertical, respectivamente, agente tem
Assim,
(b)
Resposta
(a)
(b)