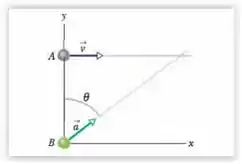
Na Fig. 4-32, a partícula se move ao longo da reta com uma velocidade constante de módulo e paralela ao eixo . No instante em que a partícula passa pelo eixo , a partícula deixa a origem com velocidade inicial zero e aceleração constante de módulo . Para que valor do ângulo entre e o semieixo positivo acontece uma colisão?
Passo 1
Bom galera , aqui temos dois corpos em movimento e eles colidem no final. Nós temos algumas informações, como a posição e velocidade inicial de ambas as partículas e também temos a aceleração de B.
E queremos saber o ângulo da direção do movimento de B!
A primeira coisa que devemos fazer é identificar os tipos de movimento que estamos trabalhando. Neste caso, a partícula descreve movimento uniforme, ou seja, com velocidade constante. No caso, o UM ou MRU. E esse movimento acontece na reta horizontal
A partícula faz um movimento uniformemente variado, ou seja, com aceleração constante. Ela parte do repouso, ou seja, tem velocidade zero no início. E a sua aceleração é de .
Agora, pra resolver... se queremos que a colisão ocorra, precisamos que as duas estejam na mesma posição ao mesmo tempo, ao final do movimento:
Podemos dizer ainda que as coordenadas da posição final de ambas serão as mesmas:
Lembrando que essa duas condições devem ocorrer simultâneamente!!!!!
Até aqui , tudo tranquilo? Vamos avaliar o movimento de cada uma das partículas separadamente aqui.
Passo 2
O enunciado nos diz que a partícula A percorre a reta . Isso significa que a sua posição vai ser sempre :
Já a posição na direção , vai depender da velocidade e do tempo :
Então:
Agora vamos calcular as coordenadas da posição final de B e igualar.
Passo 3
Como vimos no passo 1, o movimento da partícula B é um movimento uniformemente variado. Então vamos usar a equação horária da posição do MRUV (ou sorvetão) pra achar a distância total percorrida:
E como B parte da origem com velocidade zero, os dois primeiros termos somem:
Mas essa distância percorrida é na direção do movimento de B, então o que vamos fazer aqui é decompor nas direções e pra igualar às coordenadas da partícula A. Vamos relembrar onde fica o ângulo .
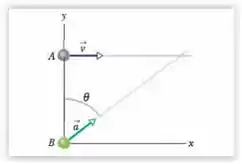
Portanto:
Agora vamos igualar às coordenadas da partícula A.
Passo 4
Bem, se as partículas colidem, então elas chegam a exata mesma posição. Como vimos no passo 1:
Igualando:
Reorganizando as duas equações:
Da relação fundamental da trigonometria:
Resolvendo por Bashkara, vamos achar que:
ACHAMOS O TEMPO TOTAL!
Agora pra achar o ângulo vamos substituir em:
E finalmente, o ângulo que tem cosseno igual a é:
Resposta
Essa questão exigiu um pouco mais de raciocínio , mas continue com a gente para dominar exercícios desse tipo