Enunciado
Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 24.7 - Ex. 20
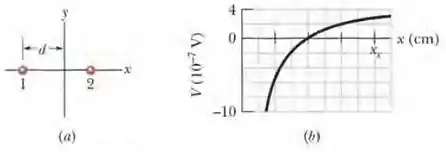
A figura (a) mostra duas partículas carregadas. A partícula 1, de carga , é mantida fixa no lugar a uma distância d da origem. A partícula 2, de carga , pode ser deslocada ao longo do eixo x. A figura (b) mostra o potencial elétrico V na origem em função da coordenada x da partícula 2. A escala do eixo x é definida por . O gráfico tende assintoticamente para para . Qual é o valor de em termos de ?
Passo 1
Olá, meu amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. A situação nos mostra que a partícula 1 é fixa, mas a partícula 2 pode se movimentar, já o gráfico da figura b nos mostra justamente o potencial elétrico no ponto de acordo com o deslocamento da partícula 2.
Não sabemos quanto vale nem , mas vamos achar o valor de sem precisar achar estes valores, usando duas informações do gráfico. Vamos ver como.
- Informação 1: Essa eu acho mais fácil de perceber: quando a partícula 2 está em x = 8,00 cm, o potencial total é zero.
- Informação 2: Essa talvez seja mais difícil de perceber: quanto a partícula 2 está no infinito, o potencial na origem depende somente da partícula 1, e o enunciado deu o valor desse potencial.
Passo 2
Vamos fazer as contas primeiro com a info. 2:
Daí, a gente tem o seguinte:
Passo 3
Agora vamos usar a info 1:
Corta o K:
Quantas cargas fundamentais isto dá? Só dividir: