Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física Volume 3 - Eletromagnetismo - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 31.4 - Ex. 14

Um indutor é ligado a um capacitor cuja capacitância pode ser ajustada através de um botão. Queremos que a frequência deste circuito LC varie linearmente com o ângulo de rotação do botão, de 2 × 10 5 H z até 4 × 10 5 H z , quando o botão gira de 180°. Se L = 1,0 m H , plote a capacitância desejada C em função do ângulo de rotação do botão.

Passo 1

Aqui temos que fazer uma função que mostre como a Capacitância muda em função do ângulo ( θ ).

Passo 2

A relação linear entre θ (o ângulo de rotação do botão, em graus) e a frequência f deve ser

f = f 0 1 + θ 180 º ⇒ f f 0 = 1 + θ 180 º

onde f 0 é a frequência mais baixa ( 2 × 10 5 H z ).

Passo 3

Como f = ω 2 π e ω = 1 L C logo f = 1 2 π L C substituindo na equação anterior temos e fazendo alguns cálculos:

1 2 π L C = f 0 1 + θ 180 º

1 f 0 1 + θ 180 º = 2 π L C

agora temos que elevar os dois lados ao quadrado

1 f 0 1 + θ 180 º 2 = 4 π 2 L C

e isolando C

C = 1 4 π 2 L f 0 2 1 + θ 180 º 2

finalmente substituindo os valores

L = 1,0 × 10 - 3 H

f 0 = 2 × 10 5 H z

C = 1 4 π 2 1,0 × 10 - 3 H × 2 × 10 5 H z 2 × 1 + θ 180 º 2 = 1 16 × 10 - 7 π 2 × 1 + θ 180 º 2

C = 1 16 × 10 - 7 π 2 × 1 + θ 180 º 2

Passo 4

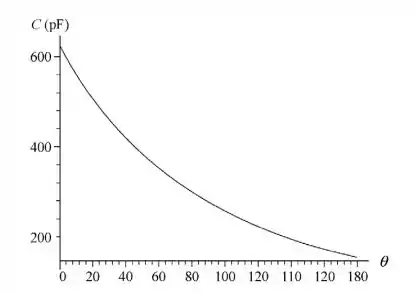
A figura a seguir mostra o gráfico da capacitância em função do ângulo de rotação.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um capacitor de 1,50 μ F é ligado, como na Fig. 31-10, a um gerador de corrente alternada com E m = 30,0V . Determine a amplitude da corrente alternada resultante se a frequência da força eletromotriz
Em um circuito L C oscilante com C = 64,0 μ F , a corrente é dada por i = ( 1,60 ) s e n ⁡ ( 2500 t + 0,680 ) , onde t está em segundos, i em ampères e a constante de fase em radianos. (a) Quanto temp
Um circuito série formado por uma indutância L 1 e uma capacitância C 1 oscila com uma frequência angular ω . Um segundo circuito série, contendo uma indutância L 2 e uma capacitância C 2 , oscila com
Qual é a capacitância de um circuito L C oscilante se a carga máxima do capacitor é 1,60 μ C e a energia total é 140 μ J ?
Em um circuito L C oscilante, a energia total é convertida de energia elétrica no capacitor em energia magnética no indutor em 1,50 μ s . Determine (a) o período das oscilações e (b) a frequência das