Exercícios de Circuitos RLC - Lista de Exercícios Resolvida
Questão 1
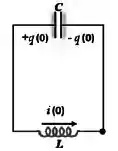
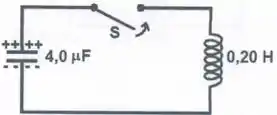
Considere o circuito abaixo com cargas e nas placas do capacitor. A chave é fechada no instante .
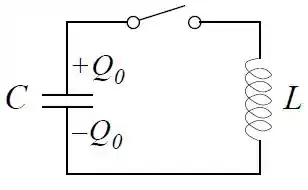
- Escreva a equação diferencia da carga na placa superior do capacitor. Explicite a condição inicial para .
- Determine a carga na placa superior e a corrente no circuito para e que satisfazem as condições iniciais.
- O indutor é formado por um solenoide muito longo de comprimento e diâmetro com voltas de fio uniformemente enroladas em um núcleo de plástico (a permeabilidade do plástico é igual à do vácuo). Calcule a indutância.
- Qual é a nova frequência angular de oscilação se o núcleo de plástico for substituído por um núcleo de ferro com permeabilidade magnética ? Expresse sua resposta em termos da frequência angular do circuito com o solenoide com núcleo de plástico.
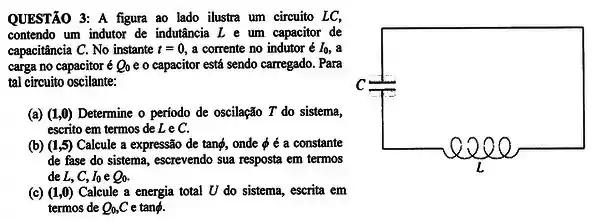
Questão 2
Um capacitor de é carregado a uma tensão de e então é ligado a um indutor de . A frequência angular de oscilação das energias armazenadas no campo elétrico do capacitor e no campo magnético do indutor é:
(a) .
(b) .
(c) .
(d) .
(e) .
Ver solução completaQuestão 3
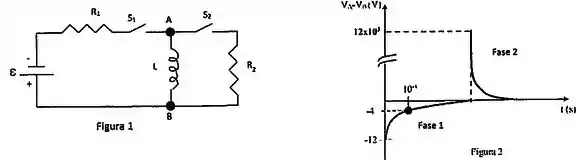
Considere o circuito da figura , onde , , , o capacitor e o indutor estão inicialmente sem energia. O circuito é operado nas seguintes fases sucessivas:
Fase : chave fechada e aberta durante longo tempo.
Fase : chave aberta e fechada durante longo tempo.
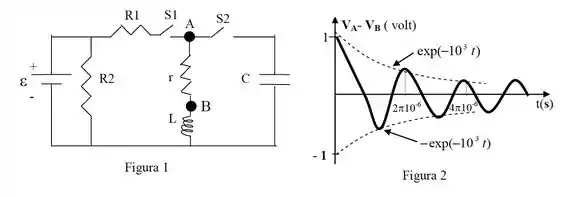
Durante a fase , a d.d.p. em função do tempo corresponde ao gráfico da figura , na qual a escala de tempo no eixo horizontal está expressa em segundos. Supondo que a frequência angular da oscilação amortecida possa ser aproximada pela da oscilação livre sem amortecimento , determine:
O valor da resistência .
O valor da corrente no indutor no final da fase .
O valor da capacitância e da indutância .
A energia dissipada na resistência na fase .
Ver solução completaQuestão 4
Considere um circuito com capacitância e indutância . Em , não há corrente passando no circuito e a tensão sobre o capacitor é de . Nas respostas numéricas abaixo, quando necessário, aproxime , e .
(a) Qual é o primeiro instante em que a corrente no indutor é máxima?
(b) Qual é o valor da corrente máxima no indutor?
(c) Após , qual é o primeiro instante em que a carga no capacitor volta a ser máxima?
Ver solução completaQuestão 5
Num circuito , e . No instante , a corrente é de , a carga do capacitor é de e o capacitor está sendo carregado.
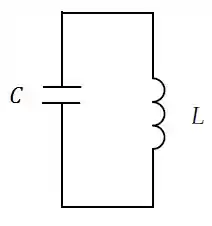
- Qual é a energia total do circuito?
- Qual é a carga máxima do capacitor?
- Qual é a corrente máxima?
- Qual é o período de oscilação da corrente no circuito?
- Sabendo-se que a carga do capacitor é dada por , qual o valor de ?
Questão 6
Considere o circuito mostrado na figura abaixo, onde o capacitor está inicialmente descarregado. Considere , , , e dados.
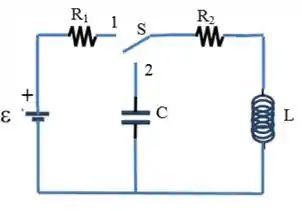
Fase I: A chave é comutada para a posição (). Nestas condições:
Escreva a expressão da corrente no circuito em função do tempo .
Após um tempo muito longo, determine as tensões sobre , e .
Fase II: A chave é comutada para a posição ().
Temos agora um circuito RLC em série onde a corrente pode ser aproximadamenre dada pela seguinte expressão: . determine os três parâmetros desta expressão: , e em função dos dados do problema (, , , e ).
Após um tempo muito longo calcule a energia total dissipada em .
Ver solução completaQuestão 7
(Esta questão compõe-se de 3 itens independentes.)
Uma bateria de constante é conectada a um indutor num circuito de malha simples. A resistência equivalente do circuito vale . No instante em que a bateria é ligada no indutor, a corrente é nula. Sabendo que a corrente que atravessa o circuito é dada pela função , calcule o valor da indutância .
Um capacitor inicialmente carregado com , é conectado a um indutor pelo qual inicialmente não passa corrente. A resistência equivalente deste circuito de malha simples vale . Encontre a expressão da carga no capacitor em função do tempo, .
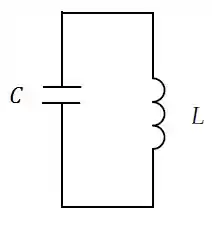
O circuito oscilante da figura possui resistência desprezível. O capacitor vale e, em , possui carga . O indutor, também em , possui energia e está sendo atravessado pela corrente com o sentido mostrado na figura. Calcule a carga máxima no capacitor.
(SUGESTÃO: Lembre-se da conservação de energia). Use
Ver solução completaQuestão 8
Em um circuito LC, no qual , a diferença de potencial máxima através do capacitor durante as oscilações é de e a corrente máxima através do indutor é de .
Encontre:
- A indutância do indutor;
- A frequência das oscilações;
- O tempo para que a carga do capacitor cresça de zero até seu valor máximo;
Questão 9
Considere o circuito da figura onde , , , e . Neste circuito ocorrem as seguintes fases sucessivas:
Fase : chave na posição durante longo tempo.
Fase : chave comutada instantanemanere da posição para a posição , permanecendo nesta posição durante longo tempo.
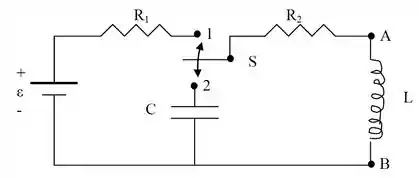
A intensidade e o sentido da corrente no indutor em função do tempo durante a Fase .
A d.d.p em função do tempo durante a Fase .
A energia armazenada no indutor no final da Fase .
A corrente no indutor em função do tempo na Fase , indicando o sentido no início desta fase ( imediatamente após a comutação da chave da posição para a posição ).
As d.d.p. , e no início da Fase .
Quais seriam os efeitos na corrente do indutor durante a Fase se os valores de e forem trocados para e , respectivamente?
Ver solução completaQuestão 10
Considere o circuito da figura 1 onde , , , , e ocorrem as seguintes fases sucessivas:
Fase1: chave fechada e aberta durante longo tempo
Fase 2: chave aberta e fechada durante longo tempo
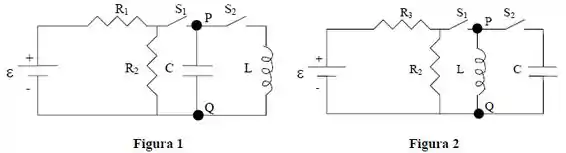
Determine, justificando todas as respostas:
A ddp em função do tempo durante a fase 2.
A corrente no indutor em função do tempo durante a fase 2.
A carga do capacitor em função do tempo durante a fase 2.
A energia do circuito durante a fase 2.
Considere agora que as posições do indutor e do capacitor são trocadas e a resistência é substituída por outra , conforme a Figura 2. Nestas novas condições, determine:
O valor da resistência tal que a energia do circuito seja igual ao da Figura 1.
Se o indutor no circuito da Figura 1 tem uma resistência interna , após quanto tempo a energia inicial do circuito decai de , sendo “ a base dos logaritmos naturais.
Ver solução completaQuestão 11
Considere o circuito ao lado com , , , e . O capacitor está inicialmente descarregado.
A chave é fechada para , produzindo uma corrente que passa através do ramo do indutor e uma corrente que passa através do ramo do capacitor.
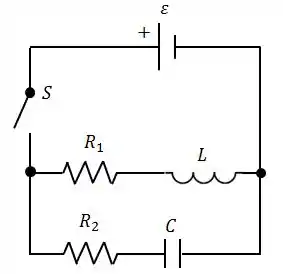
Calcule o valor de e no instante e o valor de e após um tempo muito grande após o fechamento da chave .
Escreva (indicando os valores) o comportamento das correntes e em função do tempo (a partir de ), levando em conta as diferentes constantes de tempo de cada ramo. Faça um gráfico destas correntes.
Após um tempo muito longo, a chave é aberta de novo. Desenhe o gráfico do comportamento de em função do tempo a partir da abertura de .
Qual é o valor da energia total dissipada nos dois resistores e ?
Ver solução completaQuestão 12
Considere o circuito mostrado na figura abaixo, onde o capacitor está inicialmente descarregado. Considere , , , e dados.
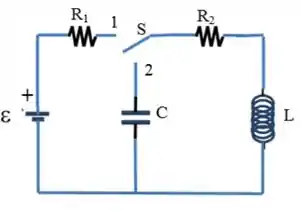
Fase I: A chave é comutada para a posição (). Nestas condições:
Escreva a expressão da corrente no circuito em função do tempo .
Após um tempo muito longo, determine as tensões sobre , e .
Fase II: A chave é comutada para a posição ().
Temos agora um circuito RLC em série onde a corrente pode ser aproximadamenre dada pela seguinte expressão: . determine os três parâmetros desta expressão: , e em função dos dados do problema (, , , e ).
Após um tempo muito longo calcule a energia total dissipada em .
Ver solução completaQuestão 13
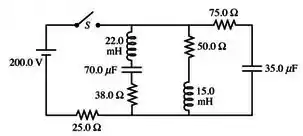
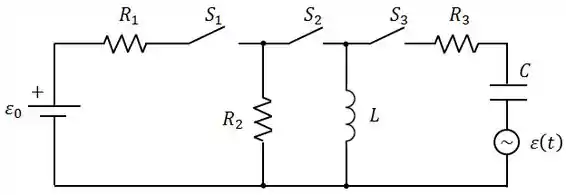
No circuito da figura abaixo, considere as seguintes fases:
Fase 1: e fechadas e aberta por um longo tempo.
Determine a corrente no indutor no início e no final da Fase 1.
Calcule a energia final armazenada no indutor .
Fase 2: e abertas e fechada durante logo tempo.
Fase 3: e abertas e é fechada.
Determine a frequência angular da fonte para que a corrente na malha tenha a maior amplitude possível.
Se , faça o diagrama dos fasores da malha e calcule o ângulo de fase entre e .
Determine a potência média fornecida pela fonte e a potência média dissipada em .
Dados: , , , , e
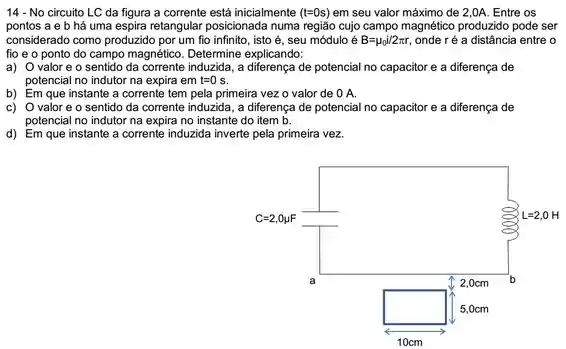
Questão 14
Um capacitor de é carregado a uma tensão de e então é ligado a um indutor de . A frequência angular de oscilação das energias armazenadas no campo elétrico do capacitor e no campo magnético do indutor é:
(a) .
(b) .
(c) .
(d) .
(e) .
Ver solução completaQuestão 15
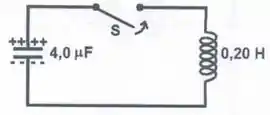
Considere o circuito abaixo com cargas e nas placas do capacitor. A chave é fechada no instante .
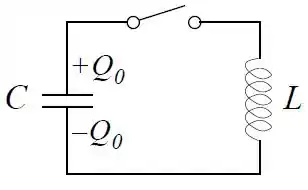
- Escreva a equação diferencia da carga na placa superior do capacitor. Explicite a condição inicial para .
- Determine a carga na placa superior e a corrente no circuito para e que satisfazem as condições iniciais.
- O indutor é formado por um solenoide muito longo de comprimento e diâmetro com voltas de fio uniformemente enroladas em um núcleo de plástico (a permeabilidade do plástico é igual à do vácuo). Calcule a indutância.
- Qual é a nova frequência angular de oscilação se o núcleo de plástico for substituído por um núcleo de ferro com permeabilidade magnética ? Expresse sua resposta em termos da frequência angular do circuito com o solenoide com núcleo de plástico.
Questão 18
Um circuito é composto por um capacitor de e um indutor de . Em o capacitor está totalmente descarregado e a corrente vale . Calcule:
- Calcular a corrente máxima no circuito.
- A carga máxima no capacitor.
- O instante em que a energia armazenada no capacitor alcança o valor máximo pela primeira vez.
Questão 19
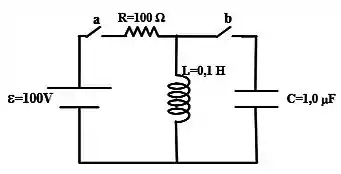
No circuito da figura a chave é fechada num determinado instante:
- Qual será a corrente inicial? Justifique.
- Qual será a diferença de potencial sobre o indutor após a chave ser fechada?
- Qual a carga máxima que o capacitor poderá atingir?
- Quanto tempo leva para o capacitor atingir a carga máxima?
segundo depois da chave ser fechada, ela é aberta e simultaneamente a chave é fechada:
Questão 20
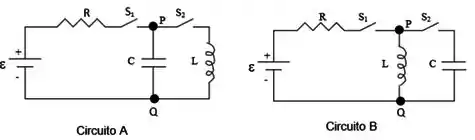
Nos circuitos e das figuras tem-se , , e , sendo que o capacitor e o indutor estão inicialmente sem energia. Nestes circuitos também ocorrem as seguintes fases sucessivas:
Fase : chave fechada e aberta durante longo tempo.
Fase : chave aberta e fechada durante longo tempo.
Com os dados a sua disposição:
Escreva a expressão da d.d.p () em função do tempo no circuito durante a Fase . Esboce também o seu gráfico nas fases e , indicando o valor no início da Fase e no início da Fase .
Escreva a expressão da d.d.p () em função do tempo no circuito durante a Fase . Esboce também o seu gráfico nas fases e , indicando o valor no início da Fase e no início da Fase .
Imagine agora que o indutor no circuito seja substituído por outro com o mesmo valor de mas cujo fio das espiras tem uma resistência total de . Escreva neste caso a expressão da d.d.p () em função do tempo durante a Fase . Faça um esboço de seu gráfico na Fase .
Ver solução completaQuestão 21
Um capacitor carregado é conectado a um indutor ideal formando um circuito com frequência angular de oscilação igual a . Considere quando o capacitor está totalmente carregado. Após um instante , a carga no capacitor é e a corrente no circuito é . Na oscilação, qual a carga máxima no capacitor?
Ver solução completa
Questão 22
No circuito abaixo, com o capacitor descarregando, a corrente atinge o seu valor máximo no instante .
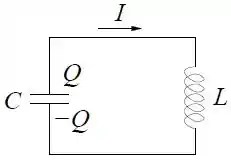
Escreva a equação diferencial para a carga na placa superior do capacitor. Usando o fato de que a corrente é máxima no instante , demostre que .
Escreva a solução geral da equação. Determine a carga e a corrente no circuito para satisfazendo as condições iniciais e .
Calcule a energia total no circuito e mostre que ela se conserva.
Ver solução completaQuestão 24
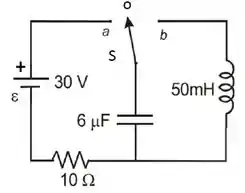
No circuito da figura ao lado, o capacitor está inicialmente descarregado e a corrente no indutor é nula. A chave está inicialmente na posição central ().
A chave passa então para a posição , onde permanece durante um tempo equivalente a duas constantes de tempo capacitivas. Em seguida (no novo instante de tempo ), passa para a posição , na qual permanece por um tempo muito longo.
- Determine a expressão da corrente que percorre o indutor em função do tempo. Qual é o valor da amplitude máxima da corrente?
- Trace os gráficos das variações da corrente no indutor e da carga no capacitor em função do tempo quando a chave está na posição .
- Determine a energia total armazenada no circuito .
Questão 25
No circuito ilustrado na figura abaixo, tanto a indutância do indutor, quanto a capacitância do capacitor são alteradas. As alternativas abaixo apresentam as variações na indutância e na capacitância. Assinale aquela que reduzirá a frequência de oscilação da corrente no circuito.
(a) e .
(b) e
(c) e .
(d) e .
(e) e .
Ver solução completaQuestão 26
A figura mostra um circuito utilizado para a geração de picos de alta tensão. Neste circuito acorrem as seguintes fases sucessivas:
Fase 1: chave fechada e aberta durante longo tempo
Fase 2: chave aberta e fechada durante longo tempo
A figura mostra o gráfico da d.d.p. durante as fases e
Com o indutor inicialmente sem corrente, determine:
- A expressão para a d.d.p. em função do tempo na fase a partir do instante de tempo no qual o interruptor é fechado. Deixe a expressão em função de , e .
- Os valores de , e sendo e assumindo (base dos logaritmos neperianos). Sugestão: utilize informações contidas no gráfico da figura considerando as fases e
- Trace o gráfico da d.d.p. em função do tempo nas fases e . Em outras palavras desenhe a nova figura para este circuito.
Supondo agora que o resistor seja retirado e no seu lugar seja colocado um capacitor . Além disso, os valores de , e são os mesmos encontrados nos itens anteriores. Com este novo circuito as fases e 2 são repetidas.
Questão 27
Considere um circuito com capacitância e indutância . Em , não há corrente passando no circuito e a tensão sobre o capacitor é de . Nas respostas numéricas abaixo, quando necessário, aproxime , e .
(a) Qual é o primeiro instante em que a corrente no indutor é máxima?
(b) Qual é o valor da corrente máxima no indutor?
(c) Após , qual é o primeiro instante em que a carga no capacitor volta a ser máxima?
(d) Considere um capacitor de placas paralelas circulares de área e distantes uma da outra. Qual é a taxa máxima de variação do campo elétrico em um ciclo de oscilação do circuito? Lembre que o campo elétrico é uniforme entre as placas com módulo de , onde é a densidade superficial de cargas sobre as placas.
(e) Qual é a densidade de corrente de deslocamento máxima entre as placas do capacitor?
(f) Qual é o campo magnético máximo em torno do capacitor a uma distância de de seu centro?
Ver solução completaQuestão 28
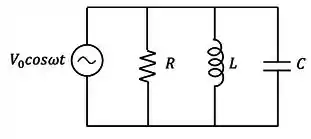
Considere o circuito de um radio FM mostrado na figura abaixo, com , e . Determine o valor aproximado da frequência da onda em que o rádio se encontra sintonizado. (usar )
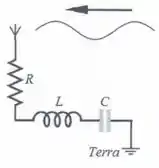
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 29
Antes de o interruptor ser fechado na figura, a ddp nos terminais do capacitor era de . Em algum instante depois do interruptor ser fechado, a corrente instantânea circulando no circuito é de . Qual é o valor da energia armazenada no campo elétrico do capacitor neste instante?
(a)
(b) .
(c) .
(d) .
(e) .
Ver solução completaQuestão 30
No circuito abaixo, um capacitor completamente carregado com capacitância igual a é conectado a um indutor de . O que acontece após a chave ser fechada?
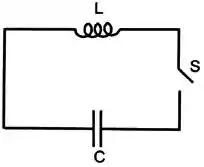
- A carga do capacitor se anula instantaneamente.
- A carga do capacitor decresce exponencialmente a zero.
- A carga permanece inalterada.
- A carga oscila com um período de .
- A carga oscila com um período de .
Questão 31
Para o circuito ilustrado na figura, o interruptor está aberto por um tempo muito longo
7a) Qual é a corrente no capacitor de no instante em que a chave é ligada?
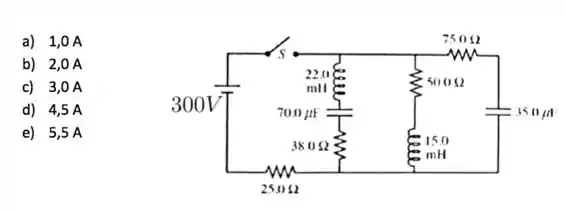
7b) Qual é a corrente no indutor de após a chave ter sido fechada por um tempo longo?
- 1,5 A
- 2,2 A
- 6,0 A
- 5,0 A
- 4,0 A
Questão 32
Uma estação de rádio FM tem sua transmissão radiofônica na frequência de . Qual deve ser o valor aproximado da indutância que deve ser ligada a um capacitor de para se construir um circuito receptor para esta estação? (Usar
Questão 33
Considere o circuito abaixo, onde e . A corrente elétrica gerada pela fonte de força eletromotriz , após o circuito ficar ligado por um tempo muito maior que a constante de tempo indutiva é:
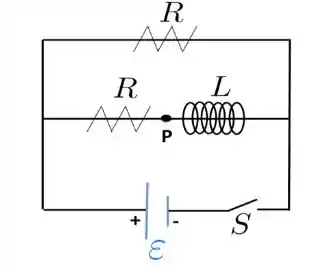
a)
b)
c)
d)
e)
Ver solução completaQuestão 34
Um circuito é formado por um indutor de , um capacitor de e uma chave . O capacitor está inicialmente carregado com uma carga . Após a chave ser fechada, o circuito começa a oscilar. Quando tempo leva para que o capacitor descarregue completamente e recarregue com a sua polarização invertida?
Questão 35
Considere o circuito da figura, onde os valores dos componentes são conhecidos: , , , e .
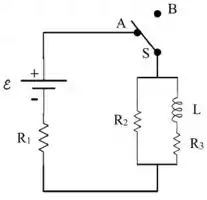
Fase 1: chave na posição A
Fase 2: chave na posição B
- Encontre as intensidades e os sentidos (para cima ou para baixo) das correntes em , e imediatamente depois de fechar a chave S na posição A (início da fase 1).
- Encontre as intensidades e os sentidos (para cima ou para baixo) das correntes em , e no final da fase 1.
- Encontre as intensidades e os sentidos (para cima ou para baixo) das correntes que passam em , e imediatamente depois de fechar a chave S na posição B (início da fase 2).
- Encontre as intensidades e os sentidos (para cima ou para baixo) das correntes que passam em , e no final da fase 2.
- Encontre a energia dissipada em cada um dos resistores , e a partir do momento que a chave S é fechada na posição B e permanece nesta posição por um tempo muito longo. (Nota: pode deixar seu resultado em termos de frações numéricas, sem necessidade de calculá-las).
Após um tempo muito longo, a chave S é colocada na posição B (fase 2).
Questão 36
Um circuito LC tem uma indutância de e uma capacitância de . No instante , a carga no capacitor é e a corrente é . A energia total é:
- ;
- ;
- ;
- ;
- ;
Questão 37
Um circuito ressonante em tem o valor de e aumentados em . A nova frequência de ressonância será:
Questão 38
A figura abaixo ilustra um circuito elétrico contendo um capacitor , um indutor e uma chave . Sabe-se que no instante , a chave é fechada, e que nesse instante, o capacitor tem carga elétrica máxima dada por e que a corrente elétrica inicial no circuito é nula . Para tal situação, determine:
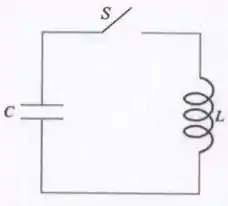
- O instante de tempo para o qual a carga armazenada no capacitor se reduz a de sua carga em .
- O instante de tempo para o qual a energia elétrica armazenada no capacitor é igual a da energia elétrica do sistema em .
Questão 39
No circuito da figura, , e o capacitor é de um tipo variável, com uma capacitância ajustável de a . O circuito é conectado a um gerado com , onde .
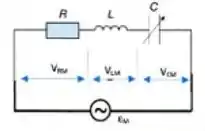
Nestas condições:
- Calcule o valor que deve assumir para se ter um fator de potência igual a .
- Calcule a amplitude da corrente.
- Calcule as amplitudes das tensões , e .
- Desenhe o diagrama de .
- Calcule o novo valor de para obter a condição de ressonância do circuito e, nesta condição, calcule os valores da potência média dissipada em e da potência média fornecida ao circuito pelo gerador.
Para colocar o circuito em condição de ressonância, você deve mudar o valor do capacitor:
Questão 40
Um circuito tem uma capacitância de e uma indutância de . No instante , a carga no capacitor é e a corrente é . A máxima carga do capacitor é:
Questão 41
6 - No circuito mostrado abaixo, o interruptor S é primeiro empurrado para cima para carregar o capacitor. Quando S é então empurrado para baixo, a corrente no circuito irá
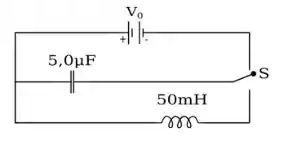
- oscilar a uma frequência de .
- oscilar a uma frequência de .
- oscilar a uma frequência de .
- diminuir exponencialmente com um tempo característico de .
- diminuir exponencialmente com um tempo característico proporcional a .
Questão 42
Num circuito , e . No instante , a corrente é de , a carga do capacitor é de e o capacitor está sendo carregado.
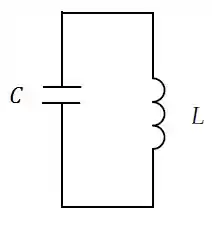
- Qual é a energia total do circuito?
- Qual é a carga máxima do capacitor?
- Qual é a corrente máxima?
- Qual é o período de oscilação da corrente no circuito?
- Sabendo-se que a carga do capacitor é dada por , qual o valor de ?
Questão 44
Uma fonte de fem alternada, com uma certa amplitude e frequência , é ligada separadamente a um resistor, a um capacitor e a um indutor. Depois que a fonte é ligada, faz-se variar e mede-se a amplitude da corrente resultante. A variação de com é mostrada no gráfico abaixo. A correspondência exata entre as curvas da figura e os dispositivos é:
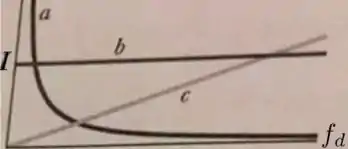
- indutor ; resistor ; capacitor;
- indutor ; resistor ; capacitor;
- indutor ; resistor ; capacitor;
- indutor ; resistor ; capacitor;
- indutor ; resistor ; capacitor;
Questão 45
3) Um capacitor é carregado por uma bateria de 12V. Em seguida, no instante , é ligado a um indutor. O gráfico mostra o comportamento da corrente no circuito em função do tempo . A partir do gráfico, determine:
a) A frequência de oscilação da corrente.
b) Os valores da capacitância e da indutância .
c) A carga máxima do capacitor.
d) As expressões para as energias armazenada no capacitor e , no indutor.
e) Faça um gráfico das tensões no indutor e no capacitor em função do tempo para o intervalo de tempo . Pode ser apenas um esboço, mas use o gráfico ao lado como um guia de formato.
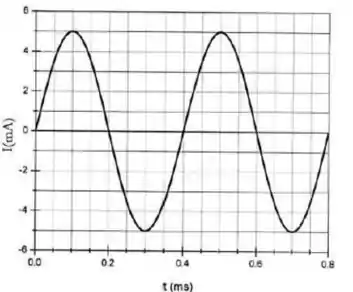 f dz
f dz
Questão 46
08) Antes do interruptor ser fechado no circuito ilustrado na figura, a ddp nos terminais do capacitor é de . Em algum instante depois de o interruptor ser fechado, a corrente instantânea vale . Qual é o valor da energia armazenada no campo elétrico do capacitor neste instante?
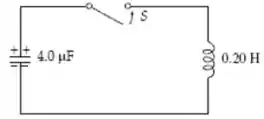
a)
b)
c)
d)
e)
Ver solução completaQuestão 47
No circuito abaixo, o capacitor tem uma capacitância e foi inicialmente carregado a uma diferença de potencial com a polaridade indicada na figura. Ele forma uma espira retangular, de lados e ao ser ligado em série a um resistor de resistência e a uma chave . A espira menor tem dimensões e , está afastada da espira maior por uma distância , possui voltas e é composta de um fio cuja resistência por unidade de comprimento vale . A figura não está desenhada em escala e é assumido que somente o fio da espira grande, mais próximo da espira pequena, produz campo magnético apreciável sobre esta (, e , portanto pode ser considerado um fio muito longo). Para todas as perguntas abaixo, desconsidere o fluxo criado pela bobina menor na bobina maior, bem como o fluxo criado pela bobina maior nela mesma. Nestas condições, encontre
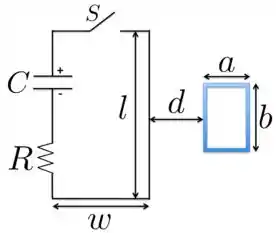
- A corrente na espira maior em função do tempo depois que a chave é fechada;
- O sentido da corrente induzida na espira menor (indique na figura e justifique);
- A corrente induzida na espira menor em função do tempo depois que a chave foi fechada.
Questão 48
Considere o circuito da figura , onde , , , o capacitor e o indutor estão inicialmente sem energia. O circuito é operado nas seguintes fases sucessivas:
Fase : chave fechada e aberta durante longo tempo.
Fase : chave aberta e fechada durante longo tempo.
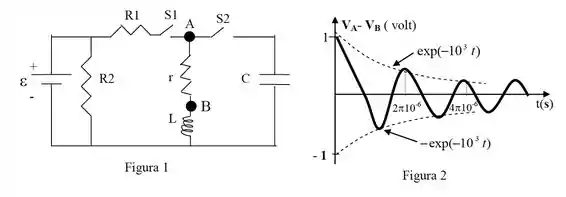
Durante a fase , a d.d.p. em função do tempo corresponde ao gráfico da figura , na qual a escala de tempo no eixo horizontal está expressa em segundos. Supondo que a frequência angular da oscilação amortecida possa ser aproximada pela da oscilação livre sem amortecimento , determine:
O valor da resistência .
O valor da corrente no indutor no final da fase .
O valor da capacitância e da indutância .
A energia dissipada na resistência na fase .
Ver solução completaQuestão 49
Um gerador de com e operando a provoca oscilações em um circuito em série que possui e . Determine:
Um segundo capacitor com a mesma capacitância é então ligado em série com os demais componentes.
determine se os valores de e aumentam, diminuem ou permanecem os mesmos.
Ver solução completaQuestão 50
Muito tempo após o fechamento da chave , ela é aberta e, simultaneamente, apenas a chave é fechada, dando início à FASE 2 (a chave continua aberta). Observou-se que a corrente no circuito relevante varia em função do tempo (medido em segundos a partir do início da FASE 2) de acordo com a expressão , sendo e , tendo sentido consistente com o determinado no item (a). Observe que resulta da derivada em relação ao tempo da expressão para a carga no capacitor C1: . Com base nestas informações:
c) Determine os valores de e .
d) Determine o valor do módulo das cargas iniciais no capacitor , indicando se a carga positiva está na sua placa superior ou inferior.
Questão 51
Em um circuito , tem-se uma bobina de indutância e uma resistência de Se o circuito está conectado em série a uma fonte de força eletromotriz de , qual será a energia armazenada no campo magnético após a corrente atingir o seu valor máximo?
Questão 52
Considere as seguintes afirmações sobre um circuito LC ideal:
I - A diferença de potencial elétrico no indutor é máxima quando a corrente elétrica que o atravessa é máxima.
II - A energia armazenada no capacitor é nula quando a corrente elétrica que o atravessa é máxima.
III - A energia armazenada no indutor é nula quando a corrente elétrica que o atravessa é nula.
São CORRETAS as afirmações:
- I e II
- II e III
- I e III
- I, II e III
- II, apenas.
Questão 53
Um gerador de com e operando a provoca oscilações em um circuito em série que possui , e . Determine:
e) A potência dissipada no resistor.
f) O circuito é predominantemente capacitivo ou indutivo.
Ver solução completaQuestão 54
Considere o circuito LC ideal ilustrado na figura abaixo. O capacitor é previamente carregado com a chave na posição 'a'. Analise as seguintes afirmações sobre o circuito após a chave ser girada para a posição 'b':
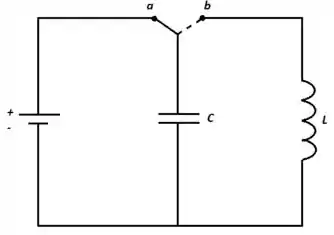
I - A diferença de potencial elétrico no indutor é máxima quando a corrente elétrica é máxima;
II - A energia armazenada no capacitor é nula quando a corrente elétrica é máxima;
III - A energia armazenada no indutor é nula quando a corrente elétrica é nula.
São CORRETAS as afirmações:
A) I e II
B) II e III
C) I e III
D) I, II e III
E) II, apenas
Ver solução completaQuestão 55
Medidas realizadas no circuito em série mostrado na Figura 1 revelaram que e , , , e . Adicionalmente, sabe-se que apenas uma das relações é verdadeira: ou .
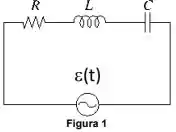
(a) (0,5) Indique, justificando, a relação verdadeira.
(b) (1,0) Represente o diagrama fasorial para o circuito, de tal forma que os fasores correspondentes a tensões () estejam em escala e que o fasor corrente, a defasagem entre a corrente e a fem estejam representados.
(c) (1,0) Determine os valores de , e .
(d) (0,5) Apresente expressões completas para e
(e) (0,5) O indutor é trocado por outro, com indutância igual a . Os seguintes elementos do circuito permanecem inalterados:, e . Determine a nova capacitância que torna o circuito ressonante, assim como o novo valor de .
Ver solução completaQuestão 56
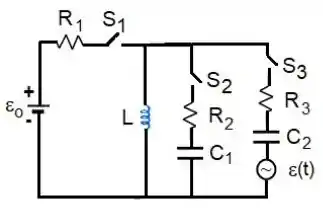
No circuito da figura, tem-se , , , e . Inicialmente o capacitor está descarregado e o indutor está sem energia. No circuito, ocorrem as seguintes fases sucessivas:
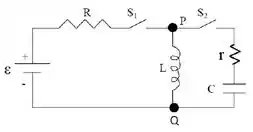
Fase 1: chave fechada e aberta durante longo tempo.
Fase 2: chave aberta e fechada durante longo tempo.
- Encontre a expressão para a corrente no indutor em função do tempo durante a Fase 1.
- Determine o valor do coeficiente de amortecimento , da frequência angular e da fase .
- Escreva a expressão geral para a corrente em função do tempo durante a Fase 2, usando os valores obtidos no item a), assim como os valores para a corrente inicial e para .
- Desenhe o circuito sem a fonte, indicando o sentido da corrente inicial e as polaridades das tensões em todos os seus elementos. Em seguida, determine expressões para as tensões no resistor e no capacitor em função do tempo durante a Fase 2.
Sabe-se que a carga no capacitor durante a Fase 2 tem a seguinte expressão geral (aqui o tempo é medido a partir do fechamento da chave ):
Questão 57
Um circuito RLC em série é alimentado por uma fonte de C.A. de e possui frequência ajustável. Quando o circuito se encontra em ressonância, a corrente de pico vale e a ddp no indutor de indutância vale . Portanto, a resistência e a capacitância valem:
A)
B)
C)
D)
E)
Ver solução completaQuestão 58
Um capacitor e uma indutor estão ligados em série. No instante , a corrente é zero, mas o capacitor está carregado. Em termos do período das oscilações deste circuito LC, o próximo instante após em que a corrente é máxima é:
a) .
b) .
c) .
d)
e) .
Ver solução completaQuestão 59
Uma fonte aplica ao circuito abaixo uma diferença de potencial . Considere ainda a impedância do circuito. A corrente que passa através do indutor será:
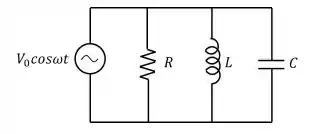
a)
b)
c)
d)
e)
Ver solução completaQuestão 60
Um indutor em um circuito RLC em série é monitorado por um voltímetro e um amperímetro de forma que o gráfico da corrente e voltagem através dele são visualizados na figura a seguir. Sabendo-se que o circuito encontra-se em ressonância, determine a capacitância do capacitor.
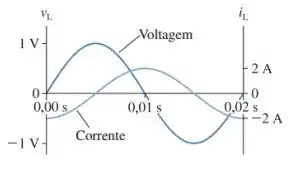
A)
B)
C)
D)
E)
Ver solução completaQuestão 61
A figura mostra um gerador de corrente alternada ligado aos terminais de uma caixa preta. A caixa contém um circuito , possivelmente com mais de uma malha, cujos elementos e ligações são desconhecidos. Medições realizadas do lado de fora da caixa revelam que:
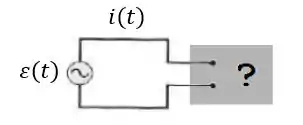
Com estas informações podemos afirmar que:
a) a corrente está adiantada em relação a e o circuito apresenta características indutivas ().
b) a corrente está adiantada em relação a e o circuito apresenta características capacitivas ().
c) a corrente está atrasada em relação a e o circuito apresenta características indutivas ().
d) a corrente está atrasada em relação a e o circuito apresenta características capacitivas ().
e) a corrente está em fase com a e o circuito apresenta características resistivas .
Ver solução completaQuestão 64
Qual das afirmativas está correta?
- Quando conectado a um capacitor carregado, um indutor conduz uma corrente constante.
- Indutores armazenam energia armazenando carga.
- Quando um indutor e um resistor estão conectados em série a uma bateria DC, a corrente no circuito é reduzida a zero em uma constante de tempo.
- Quando conectado a um circuito, um indutor sempre resiste à qualquer variação de corrente através dele.
- Quando um indutor e um resistor estão conectados em série a uma bateria, a corrente no circuito é zero depois de um tempo muito longo.
Questão 65
Um solenoide de autoindutância é percorrido por uma corrente estacionária .
Qual é o valor da energia magnética armazenada no indutor?
Por meio de um chaveamento, no instante , o indutor é colocado em série com um capacitor de capacitância de modo a formar um circuito . A corrente inicial no indutor é e a carga inicial no capacitor é . Use a lei de conservação de energia para determinar a carga máxima que pode ser atingida no capacitor.
Escreva a equação diferencial para a carga do capacitor e determine a frequência angular de oscilação .
Ver solução completaQuestão 66
Considere o circuito formado por uma bateria com fem , um resistor com resistência , um capacitor com capacitância , um indutor com indutância e uma chave comutadora com duas posições: e .
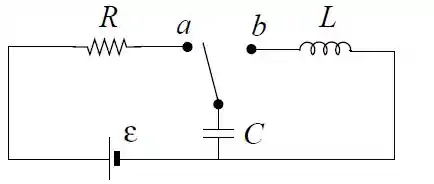
A chave permanece na posição por um tempo muito longo. Nesta situação, em um instante definido como , a chave passa para a posição b.
Qual é a carga na placa superior do capacitor em .
Deduza a equação diferencial para a carga na placa superior do capacitor com a chave na posição . Sabendo que a solução geral da equação diferencial tem a forma , determine . Usando as condições iniciais para o problema determine e .
Determine a energia no capacitor e a energia no indutor como função do tempo. A soma das energias no capacitor e no indutor depende do tempo?
Ver solução completaQuestão 68
Em um circuito LC, no qual , a diferença de potencial máxima através do capacitor durante as oscilações é de e a corrente máxima através do indutor é de .
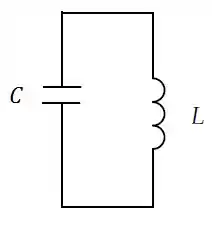
Encontre:
- A indutância do indutor;
- A frequência das oscilações;
- O tempo para que a carga do capacitor cresça de zero até seu valor máximo;
Questão 69
14 - Um capacitor e um indutor estão conectados em série, conforme mostra a figura. No instante a corrente elétrica no circuito é nula, mas o capacitor está totalmente carregado.

Se T é o período de oscilação, a próxima vez, após t=0, que a tensão no indutor será máxima ocorre no instante
Questão 70
(Esta questão compõe-se de 3 itens independentes.)
Uma bateria de constante é conectada a um indutor num circuito de malha simples. A resistência equivalente do circuito vale . No instante em que a bateria é ligada no indutor, a corrente é nula. Sabendo que a corrente que atravessa o circuito é dada pela função , calcule o valor da indutância .
Um capacitor inicialmente carregado com , é conectado a um indutor pelo qual inicialmente não passa corrente. A resistência equivalente deste circuito de malha simples vale . Encontre a expressão da carga no capacitor em função do tempo, .
O circuito oscilante da figura possui resistência desprezível. O capacitor vale e, em , possui carga . O indutor, também em , possui energia e está sendo atravessado pela corrente com o sentido mostrado na figura. Calcule a carga máxima no capacitor.
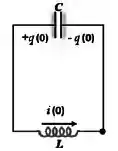
(SUGESTÃO: Lembre-se da conservação de energia). Use
Ver solução completaQuestão 72
Ordene as constantes de tempo dos três circuitos abaixo, da maior para a menor. Considere todas as resistências e indutâncias com iguais valores respectivamente.
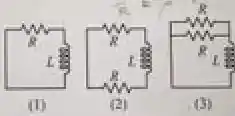
Questão 73
Na figura ao lado, , e e a fonte ideal tem uma força eletromotriz . A chave é mantida na posição durante um longo tempo antes de ser colocada na posição . Assinale abaixo a alternativa que indica a amplitude das oscilações da corrente, , no circuito após a chave ser colocada na posição .
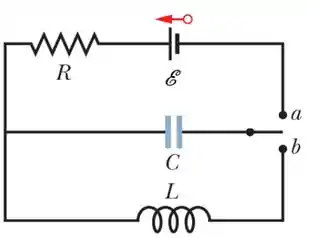
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 74
Um “dimmer” é um dispositivo que permite variar a intensidade luminosa de uma lâmpada. Estes dispositivos são compostos por uma bobina de indutância variável em série com uma lâmpada (Figura 1). A lâmpada é o elemento resistivo do circuito. O valor da indutância da bobina pode assumir qualquer valor entre e .
O circuito da Figura 1 é alimentado por um gerador alternado com uma f.e.m. eficaz e uma frequência angular . Considere que a potência média dissipada pela lâmpada não pode exceder e que a sua resistência elétrica é constante (não varia nem com a temperatura nem com outros fatores).
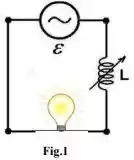
a) Calcule qual deve ser o valor mínimo da indutância no intervalo fornecido para que a potência média dissipada na lâmpada seja máxima . Calcule também o valor da resistência da lâmpada.
b) Calcule qual deve ser o valor da indutância para que a potência média dissipada pela lâmpada seja .
c) Se no lugar do gerador de f.e.m. alternada fosse inserida uma bateria de corrente continua , qual deveria ser o valor da tensão para que, decorrido um tempo muito longo, a potência dissipada na lâmpada fosse de ?
Considere novamente o circuito da Figura 1. Agora a lâmpada é substituída por um resistor e no circuito é inserido em série um capacitor .
d) (0,5) Considerando que a indutância possui o valor máximo calculado no item (b) desenhe o diagrama de fasores do circuito. A corrente que passa no circuito está adiantada ou atrasada em relação à tensão do gerador?
e) (1,0) Variando o valor da indutância L entre os limites permitidos, e , é possível fazer com que o circuito entre em ressonância? No caso de resposta negativa, justifique. No caso de resposta afirmativa, calcule o valor de para que isso aconteça.
Ver solução completaQuestão 75
Considere o circuito abaixo, onde é um capacitor de , um indutor de , e .
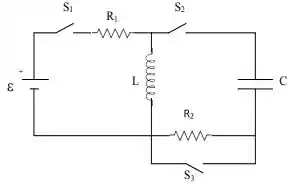
Fase 1: Chave fechada, com e abertas. O capacitor está totalmente descarregado. Determine:
a) A corrente no indutor após longo tempo com fechada e e abertas;
b) A energia transferida pela bateria ao indutor após longo tempo com fechada.
Fase 2: Depois de muito tempo, a chave é aberta e e são fechadas. Supondo quando e são fechadas, determine:
c) A expressão da corrente instantânea no indutor em função do tempo, a partir deste instante;
d) A diferença de potencial em a partir deste instante;
e) A soma das energias instantâneas armazenadas no capacitor e no indutor a partir deste instante. Justifique.
Fase 3: Se, após algum tempo, é aberta, permanecendo fechada e aberta, determine:
f) A carga no capacitor e a corrente no indutor um longo tempo após a abertura de ;
g) A energia dissipada no resistor um longo tempo após a abertura de . Justifique.
Ver solução completaQuestão 76
No circuito RLC em série e sem fonte da Figura 1, , e . No instante , a corrente no circuito é , a carga no capacitor é e o capacitor está sendo carregado (isto é, a carga é positiva e aumenta).
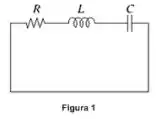
Inicialmente, suponha que o resistor não existe.
(a) Determine a carga máxima no capacitor.
(b) Determine a corrente máxima no circuito.
(c) Se a carga no capacitor é dada por , determine o ângulo de fase .
Em seguida, considere a existência do resistor.
(d) Apresente, justificando, a nova expressão para . Em seguida, apresente um algoritmo (um procedimento detalhado, mas sem realizar as contas) para a determinação dos parâmetros e a partir dos dados do problema (, , , , ).
Ver solução completaQuestão 78
Muito tempo após o fechamento das chaves e , elas são abertas e a chave é fechada, dando início à FASE 2. Esta comutação é realizada de forma simultânea, não havendo perdas nas energias armazenadas no indutor e no capacitor. Com base nestas informações:
e) Determine de forma literal expressões para a carga no capacitor e a corrente no circuito relevante em função do tempo (medido em segundos a partir do início da FASE 2), de e, assim como da corrente inicial e da carga inicial no capacitor.
f) Determine de forma numérica expressões para a carga no capacitore a corrente no circuito relevante em função do tempo (medido em segundos a partir do início da FASE 2), usando os valores de e, assim como da corrente inicial e da carga inicial no capacitor, obtidos nos itens anteriores.
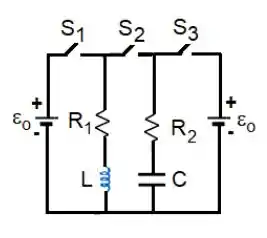
Questão 79
Q - Um circuito série está conectado a uma fonte de tensão alternada . A resistência tem valor , a indutância é e a capacitância é .
O circuito é mais capacitivo ou mais indutivo? Justifique.
Qual é a amplitude da corrente no circuito?
Para que valor deve ser ajustada a frequência da fonte de modo que a amplitude da corrente permaneça a mesma ao dobrarmos a capacitância?
Ver solução completaQuestão 80
O circuito LC oscilante representado na figura abaixo (despreze qualquer efeito dissipativo) é formado por um capacitor com capacitância e um indutor com indutância . Neste circuito, verifica-se que a tensão (diferença de potencial) máxima obtida é de .
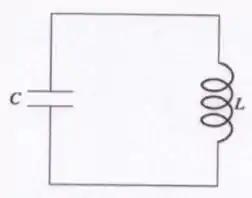
- Partindo do princípio de conservação da energia eletromagnética, obtenha a equação diferencial ordinária de segunda ordem que descreve a evolução temporal da carga no capacitor; a partir do resultado obtido em obtenha a frequência de oscilação (onde é a frequência angular do sistema) das cargas e da corrente neste circuito LC.
- Calcule o valor da carga máxima no capacitor e da corrente máxima no circuito.
- Calcule o valor da energia máxima armazenada no campo magnético do indutor.
Questão 83
Um capacitor e um indutor são ligados em série. No instante a corrente é zero, mas o capacitor está carregado. Em termos do período das oscilações do circuito, o próximo instante após em que a carga no capacitor é máxima é:
Questão 84
Um circuito LC é construído com um indutor de e um capacitor de . No instante , a carga no capacitor era nula e a corrente máxima, igual a . Quanto tempo decorre até o capacitor ficar completamente carregado?
Questão 85
2.4) O valor finito da resistividade elétrica dos dielétricos utilizados nos capacitores resulta
em correntes não nulas entre as placas do capacitor, denominadas correntes de fuga. Considere um capacitor de placas planas paralelas preenchido com um dielétrico de constante
dielétrica e resistividade . Uma figura de mérito do capacitor é o produto , denominado constante de tempo, onde é a resistência elétrica e é a capacitância.
(a) Através de uma análise dimensional, mostre que possui dimensão de tempo.
Ver solução completaQuestão 86
2.4) O valor finito da resistividade elétrica dos dielétricos utilizados nos capacitores resulta
em correntes não nulas entre as placas do capacitor, denominadas correntes de fuga. Considere um capacitor de placas planas paralelas preenchido com um dielétrico de constante
dielétrica e resistividade . Uma figura de mérito do capacitor é o produto , denominado constante de tempo, onde é a resistência elétrica e é a capacitância.
(b) Mostre que, se o capacitor estiver carregado com carga , a corrente de fuga será igual
a .
Ver solução completaQuestão 87
2.4) O valor finito da resistividade elétrica dos dielétricos utilizados nos capacitores resulta
em correntes não nulas entre as placas do capacitor, denominadas correntes de fuga. Considere um capacitor de placas planas paralelas preenchido com um dielétrico de constante
dielétrica e resistividade . Uma figura de mérito do capacitor é o produto , denominado constante de tempo, onde é a resistência elétrica e é a capacitância.
(c) Mostre que .
Ver solução completa