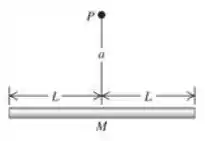
A massa está uniformemente distribuída ao longo de uma linha de comprimento igual a . Uma partícula de massa está localizada a uma distância acima do centro da linha sobre sua bissetriz ortogonal (Ponto da Figura ). Ache os componentes perpendiculares e paralelos à linha da força gravitacional que a linha exerce sobre a partícula. O seu resultado se reduz a uma expressão correta quando assume valores muito elevados?

Se nós queremos encontrar a força gravitacional que a linha exerce sobre a partícula, conhecemos essa força e ela é dada por:

Onde a distância entre as duas massas é dada por , então precisamos encontrar essa distância no nosso problema. Olha pra nossa figura novamente:

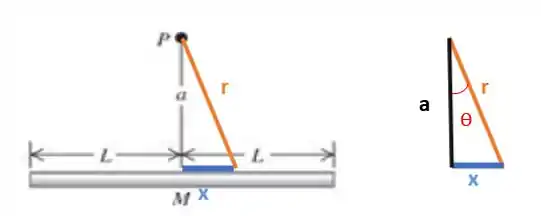
Vamos considerar um pedacinho de massa a uma distância do centro da barra, você concorda comigo que por esse desenho que eu fiz aí em cima, a distância ao quadrado até esse pedaço de massa vai ser , certo?

Daí se diferenciarmos a força gravitacional em relação a massa, nós teremos:

E substituindo nosso diferencial de massa:

Ficamos assim:

Mas a componente que vai sobrar é a componente vertical, não vai sobrar nenhuma componente horizontal . E sabemos (de outros carnavais kkk) que a força vertical é multiplicada por

Nós estamos multiplicando por 2, pois temos os dois lados da barra que são simétricos e compõem essa força vertical, não esquece disso!

Agora vamos juntar tudo isso e colocar na integral!

Como já estou somando vezes a força resultante, meus limites de integração nessa barra vão de até . Daí a integral da força fica assim ó:

E consultando numa tabela de integrais, ficamos com essa expressão aqui pra força:

Substituindo os limites de integração:

Cortando o L de cima com o L de baixo e a distância que também estava no numerador e no denominador:

Quando temos , podemos desprezar no denominador, e aquela raiz ali fica parecendo , daí a força fica com uma cara bem conhecida:

Como é o esperado!