Enunciado
Física - Fundamentos de Física - Mecânica Volume 1 - 8ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 8º - Capítulo 10.Problemas Adicionais - Ex. 96
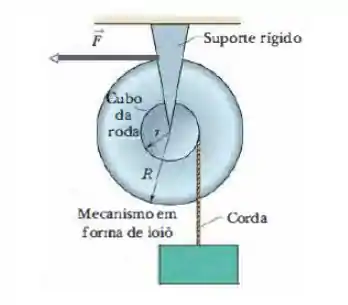
Um mecanismo em forma de ioiô, montado em um eixo horizontal sem atrito, é usado para levantar uma caixa de , como mostra a figura abaixo. O raio externo da roda é e o raio do cubo da roda é . Quando uma força horizontal constante de módulo é aplicada a uma corda enrolada na roda, a caixa, que está pendurada em uma corda no cubo, tem uma aceleração para cima de módulo . Qual é o momento de inércia do mecanismo em relação ao eixo de rotação?
Passo 1
Olá pessoal, tudo bem? Bora resolver essa questão? A imagem que o enunciado nos dá, é essa aqui:
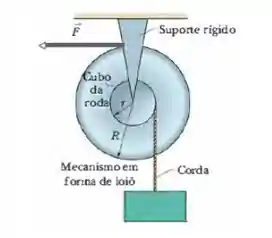
Então primeira coisa é analisar o que está acontecendo no sistema. Temos uma força que faz o sistema se movimentar para cima e uma força peso (), aplicada na caixa, diretamente para baixo. Essas duas forças produzem rotações em sentidos contrários, sendo assim, devemos nos atentar ao sinal delas. A corda também está sob ação de uma tração , atuando somente o eixo , tal que:
Logo:
Onde é a aceleração resultante dada pelo enunciado como . Xuxu beleza? Então bora lá ver que que acontece nessa brincadeira!!
Passo 2
Agora uma equação que nos fornece uma relação com o momento de inércia e a força resultante, é a equação para o torque, dada como:
Onde é a aceleração angular resultante, expressa por:
Já o torque, pode ser escrito como produto entre as forças e o raio que elas atuam, de forma que:
Onde é a força aplicada na horizontal e é a tração no fio.
Passo 3
Então juntando todas essas informações, obtemos que:
Dando mais uma arrumadinha:
De forma que colocando em evidência, obtemos:
Substituindo os valores:
