Exercícios de Rolamento sem Deslizamento - Lista de Exercícios Resolvida
Questão 1
Aplica-se uma força de 3000N a um rolo compressor que tem a forma de um cilindro maciço uniforme de raio 0,5m e massa 1000kg, conforme a figura. O cilindro rola sem deslizar sobre uma superfície horizontal. A aceleração do centro de massa e coeficiente de atrito mínimo para impedir o deslizamento valem , respectivamente:
a)
b) 3
c)
d)
e)
Questão 2
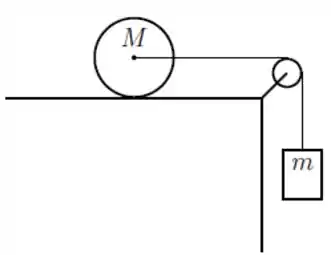
Um cilindro rígido e homogêneo de massa e raio está sobre uma superfície horizontal e pode girar livremente em torno de seu eixo de simetria longitudinal, como indicado na figura. O eixo está preso a uma extremidade de um fio ideal que passa por uma polia ideal e tem em sua outra extremidade um bloco suspenso de massa . O bloco desce verticalmente com aceleração para baixo e o cilindro rola sem deslizar sobre a superfície horizontal devido ao seu atrito com ela. O momento de inércia do cilindro relativo ao eixo de simetria é . Considere como dados e o módulo da aceleração da gravidade.
a) Indique todas as forças externas que atuam sobre o bloco e sobre o cilindro.
b) Calcule o módulo da aceleração do bloco;
c) Calcule o módulo da força de atrito sobre o cilindro e indique o seu sentido.
Ver solução completaQuestão 3
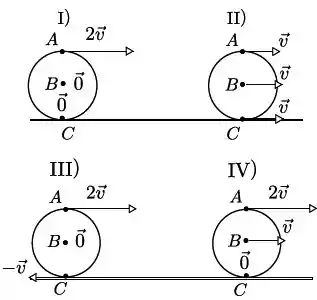
Um cilindro solido rola sem deslizar, com velocidade angular constante, sobre uma superfície horizontal. Dentre os diagramas abaixo, , , e , aquele que representa corretamente os vetores velocidade (indicados por setas) dos pontos (topo), (base) e (centro), pontos pertencentes a periferia do cilindro (seção reta), em relação a um referencial fixo na Terra é
- Nenhum deles
Questão 4
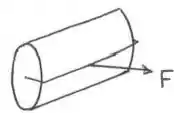
Um cilindro maciço de massa e raio é acelerado por uma força de tração , conforme mostrada na figura, aplicada através de uma corda enrolada em torno de um tambor de raio conectado concentricamente ao centro do cilindro. Despreze a massa da corda e do tambor e assuma o movimento na horizontal. O coeficiente de atrito estático é suficiente para que o cilindro role sem deslizar. Considerando que a aceleração do cilindro é e que o momento de inércia é :
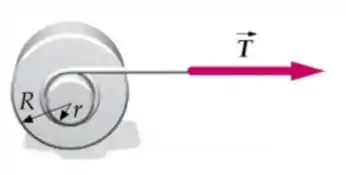
Determine a força de atrito em função de ,,,.
Qual valor de para que a aceleração do cilindro seja maior que .
Ver solução completaQuestão 5
Um cilindro homogêneo, de raio e massa , rola sem deslizar sobre um plano horizontal,
deslocando-se com velocidade , até alcançar um plano com inclinação , continuando a rolar sem deslizamento, descendo ao longo de um comprimento até atingir um novo plano horizontal.
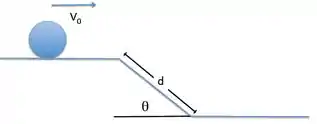
a) Qual o trabalho realizado no processo pela força peso?
b) Qual a velocidade do cilindro na base do plano inclinado?
Ver solução completaQuestão 6
Na figura abaixo, temos dois cilindros 1 e 2 que se movem puxados por uma força . Os dois cilindros são idênticos, e seus centros estão ligados por uma corda ideal. Os rolamentos são sem deslizamento. Podemos afirmar que:
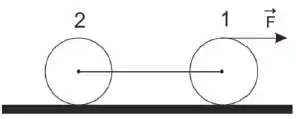
a) A força de atrito sobre o cilindro 1 está no mesma direção e sentido da força , e a força de atrito sobre o cilindro 2 está na mesma direção e sentido oposto a esta força.
b) As forças de atrito sobre os cilindros 1 e 2 estão na mesma direção e mesmo sentido da força .
c) A força de atrito sobre o cilindro 1 está na mesma direção e sentido oposto ao da força , e a força de atrito sobre o cilindro 2 está na mesma direção e mesmo sentido desta força.
d) As forças de atrito sobre os cilindros 1 e 2 estão na mesma direção e mesmo sentido, oposto ao da força .
e) N.D.A.
Ver solução completaQuestão 7
Um cilindro solido rola sem deslizar, com velocidade angular constante, sobre uma superfície horizontal. Dentre os diagramas abaixo, , , e , aquele que representa corretamente os vetores velocidade (indicados por setas) dos pontos (topo), (base) e (centro), pontos pertencentes a periferia do cilindro (seção reta), em relação a um referencial fixo na Terra é
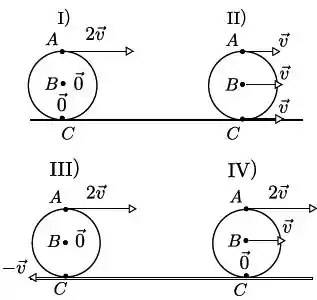
- Nenhum deles
Questão 8
Um disco de massa e raio está em repouso sobre uma superfície plana, horizontal e com atrito. Num dado instante aplica-se no seu centro uma força constante, cuja direção faz um ângulo com a horizontal, como mostra a figura. Sabe-se que o disco rola sem deslizar sobre a superfície e que o momento de inércia do disco em relação a um eixo perpendicular ao plano do disco e que passa pelo seu centro é .
Considere a resistência do ar desprezível, e que a gravidade tem módulo conhecido.
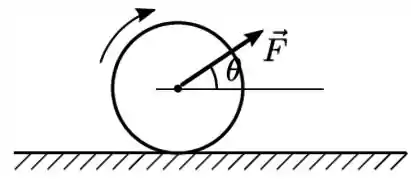
a) Faça um diagrama representando todas as forças que agem sobre o disco nos seus respectivos pontos de aplicação.
b) Determine o módulo da aceleração, , do centro de massa do disco enquanto ele se desloca.
c) Determine o módulo e o sentido da força de atrito que atua sobre o disco.
d) Determine a energia cinética adquirida pelo disco no instante em que dá uma volta completa a partir do instante inicial.
Ver solução completaQuestão 9
Uma esfera é lançada rolando sem deslizar subindo um plano inclinado com velocidade inicial do seu centro de massa. Um bloco é lançado subindo em translação um plano inclinado com a mesma inclinação e com a mesma velocidade inicial do seu centro de massa. No plano onde se encontra a esfera há atrito suficiente para que ela permaneça rolando sem deslizar e no plano onde está o bloco não há atrito.
A relação entre a altura máxima que o bloco atinge e a altura máxima que a esfera atinge nos respectivos planos é dada por
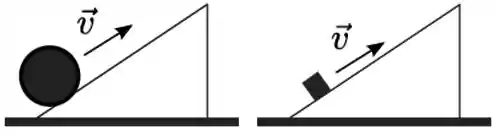
(a) , pois tanto a energia cinética do bloco como a da esfera se conserva.
(b) , pois tanto a energia mecânica do bloco como a da esfera se conserva.
(c) , pois o bloco desliza sem atrito.
(d) , pois a esfera rola sem deslizar.
(e) , pois tanto a energia mecânica do bloco como a da esfera se conserva.
Ver solução completaQuestão 10
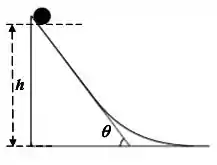
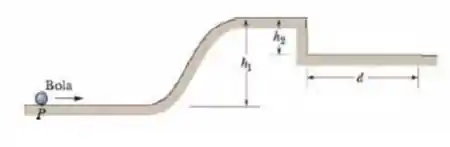
Na figura abaixo uma bola pequena, homogênea é lançada do ponto P, rola suavemente em uma superfície horizontal, sobe uma rampa e chega a um platô. Em seguida, deixa o platô horizontalmente para pousar em outra superfície mais abaixo, a uma distância horizontal da extremidade do platô. As alturas verticais são e . Com que velocidade a bola deve ser lançada do ponto P para pousar em ?
Questão 11
Um carretel de raio externo, raio interno (), massa e momento de inércia em relação ao centro de massa é puxado ao longo de um piso horizontal rugoso por um fio que exerce uma tração , conforme a figura. O coeficiente é um número adimensional e o coeficiente de atrito estático é . Suponha haver rolamento sem deslizamento. Faça corretamente o que for solicitado em função dos dados fornecidos a partir das leis físicas sobre torque e rolamento.
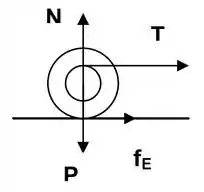
Obtenha uma expressão para o valor da aceleração do centro de massa .
Encontre uma expressão para o módulo da força de atrito estático
Agora considere que o carretel é jogado tangencialmente sobre o piso (cujo coeficiente de atrito cinético vale ) com velocidade inicial do centro de massa , no sentido positivo do eixo , e velocidade angular inicial . Não há tração nesse caso. Seja , e . Determine se no instante de tempo quando e o carretel parou de deslizar e iniciou o rolamento sem deslizamento.
Ver solução completaQuestão 12
Uma esfera de massa e raio parte do repouso e rola sem deslizar sobre uma rampa que se encontra presa no solo. Essa rampa não é plana, como indica a figura, onde também está indicado que a esfera deixa a rampa no ponto , após seu centro de massa descer uma altura desconhecida. Observa-se que o centro de massa da esfera deixa a rampa com uma velocidade horizontal de módulo e que ela atinge um solo a uma distância da base da rampa. Desconsidere o efeito da resistência do ar com a esfera e use que o momento de inércia da esfera em relação a um eixo que passa pelo CM é . Considere que a esfera não perde o contato com a rampa até atingir o ponto .
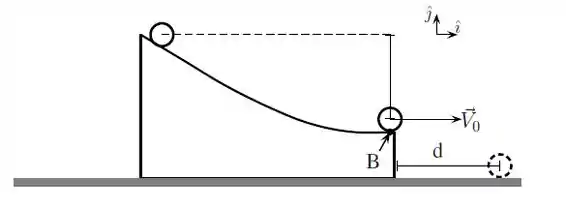
a) Qual é a diferença de altura do centro de massa da esfera entre o instante em que ela foi abandonada e aquele em que ela perde o contato com a rampa, no ponto ?
b) Qual é o trabalho realizado por cada uma das forças que atuam sobre a esfera no deslocamento do item (a)?
c) Qual é a altura do ponto em relação ao solo?
d) Usando os vetores unitários definidos na figura, determine o vetor velocidade do centro de massa da esfera no instante imediatamente anterior a atingir o solo.
e) Qual é a velocidade angular da esfera no instante de item (d)
Ver solução completaQuestão 13
Um disco, um anel e uma esfera oca, todos de massa e raio são soltos simultaneamente a partir do repouso do topo de um plano inclinado que faz um ângulo com a horizontal. Existe atrito entre o plano inclinado e os objetos. Os objetos rolam sem deslizar plano abaixo.
Assinale falso ou verdadeiro às seguintes afirmações. Neste item não é necessário justificativa.
As forças de atrito e da gravidade nos objetos apontam na mesma direção e em sentidos opostos;
O disco chegará primeiro na base do plano inclinado por que tem o menor momento de inércia;
O anel chegará primeiro na base do plano inclinado por que tem o maior momento de inércia;
Como todos tem a mesma massa e mesmo raio, todos chegarão juntos na base do plano inclinado;
Se não existisse atrito todos chegariam juntos na base do plano inclinado.
Ver solução completaQuestão 14
Um aro rola com velocidade constante e sem deslizar sobre uma superfície horizontal. Sua energia cinética de rotação em torno do centro de massa é: Dado: ICM = mr2
a) Metade de sua energia cinética de translação.
b) Igual que sua energia cinética de translação.
c) O dobro de sua energia cinética de translação.
d) Quatro vezes asua energia cinética de translação.
e) Um terço de sua energia cinética de translação.
Ver solução completaQuestão 15
(Cap. 11 – Ex. 15)
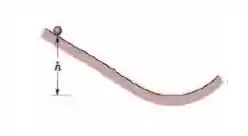
Bola não homogênea. Na figura abaixo uma bola de massa e raio rola suavemente, a partir do repouso, descendo uma rampa e passando por uma pista circular com de raio. A altura inicial da bola é . Na parte mais baixa da curva, o módulo da força normal que a pista exerce sobre a bola é . A bola é formada por uma casca esférica extrerna homogênea (com uma certa massa específica) e uma esfera central , também homogênea (mas com massa específica diferente). O momento de inércia da bola é dado pela expressão geral , mas não é igual a , como no caso de uma bola homogênea. Determine o valor de .
Questão 16
4) Uma esfera homogênea de raio e massa , ao ser abandonada do repouso do alto de uma rampa inclinada em relação à horizontal, desce rolando sem deslizar. Sendo conhecidos os coeficientes de atrito cinético e estático e entre a superfície e a esfera e o módulo Acm da aceleração para a translação do centro de massa da esfera, o módulo da força de atrito que atua sobre a esfera é dado por:
(a) .
(b)
(c)
(d) .
e) .
Ver solução completaQuestão 17
Um cilindro maciço de massa e raio é acelerado por uma força de tração , conforme mostrada na figura, aplicada através de uma corda enrolada em torno de um tambor de raio conectado concentricamente ao centro do cilindro. Despreze a massa da corda e do tambor e assuma o movimento na horizontal. O coeficiente de atrito estático é suficiente para que o cilindro role sem deslizar. Considerando que a aceleração do cilindro é e que o momento de inércia é :
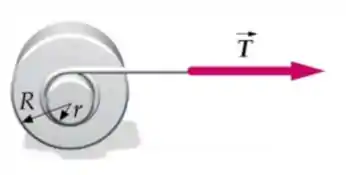
Determine a força de atrito em função de ,,,.
Qual valor de para que a aceleração do cilindro seja maior que .
Ver solução completaQuestão 18
Um cilindro homogêneo de massa e raio está em repouso sobre o topo de uma mesa. Um fio é ligado por meio de um suporte duplo preso às extremidades de um eixo sem atrito passando pelo centro do cilindro de modo que o cilindro pode girar em torno do eixo. O fio (inextensível e de massa desprezível) passa sobre uma polia em forma de disco de massa e raio montada em um eixo sem atrito que passa pelo seu centro. Um bloco de massa é suspenso na extremidade livre do fio. O fio não desliza sobre a polia e o cilindro rola sem deslizar sobre o topo da mesa. O sistema é liberado a partir do repouso.
Expresse seus resultados em termos dos dados do problema ( e ) e da aceleração da gravidade .
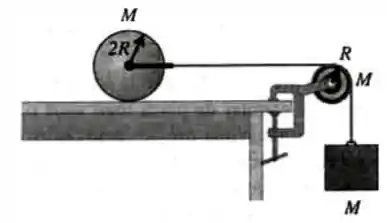
(a) Esboce diagramas de corpo livre (indicando as forças atuantes) do cilindro, da polia e do bloco.
(b) Calcule a aceleração do bloco.
(c) Determine o módulo do torque resultante na polia.
(d) Calcule o coeficiente de atrito estático entre o cilindro e a mesa.
Dados: polia de massa e raio , eixo perpendicular ao plano do disco passando pelo centro: . Cilindro de massa e raio , eixo central .
Ver solução completaQuestão 19
Aplica-se uma força de 3000N a um rolo compressor que tem a forma de um cilindro maciço uniforme de raio 0,5m e massa 1000kg, conforme a figura. O cilindro rola sem deslizar sobre uma superfície horizontal. A aceleração do centro de massa e coeficiente de atrito mínimo para impedir o deslizamento valem , respectivamente:
a)
b) 3
c)
d)
e)
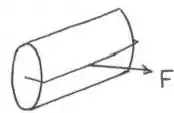
Questão 20
Uma lata vazia de altura , raio e massa , com tampa, parte do repouso e rola sem escorregar por um plano inclinado de angulo e comprimento . Considere conhecido que o momento de inércia de um disco de massa e raio em relação à um eixo perpendicular que passa pelo seu centro é .
a)Qual é o momento de inércia da lata, , em relação ao seu eixo de simetria? O resultado deve ser dado como função de . Considere a lata como sendo um cilindro com duas tampas, com densidade superficial homogênea.
b) Calcule a força de atrito sobre a lata em termos de ;
c) Calcule a aceleração do centro de massa e a aceleração angular da lata;
d) Calcule velocidade angular da lata ao chegar ao final da rampa;
e) Qual o trabalho realizado pela força de atrito? Justifique.
Ver solução completaQuestão 21
Na figura abaixo, temos dois cilindros 1 e 2 que se movem puxados por uma força . Os dois cilindros são idênticos, e seus centros estão ligados por uma corda ideal. Os rolamentos são sem deslizamento. Podemos afirmar que:
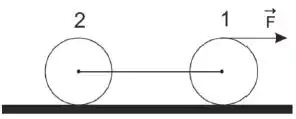
a) A força de atrito sobre o cilindro 1 está no mesma direção e sentido da força , e a força de atrito sobre o cilindro 2 está na mesma direção e sentido oposto a esta força.
b) As forças de atrito sobre os cilindros 1 e 2 estão na mesma direção e mesmo sentido da força .
c) A força de atrito sobre o cilindro 1 está na mesma direção e sentido oposto ao da força , e a força de atrito sobre o cilindro 2 está na mesma direção e mesmo sentido desta força.
d) As forças de atrito sobre os cilindros 1 e 2 estão na mesma direção e mesmo sentido, oposto ao da força .
e) N.D.A.
Ver solução completaQuestão 22
Um cilindro homogêneo, de raio e massa , rola sem deslizar sobre um plano horizontal,
deslocando-se com velocidade , até alcançar um plano com inclinação , continuando a rolar sem deslizamento, descendo ao longo de um comprimento até atingir um novo plano horizontal.
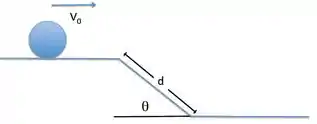
a) Qual o trabalho realizado no processo pela força peso?
b) Qual a velocidade do cilindro na base do plano inclinado?
c) Qual o coeficiente de atrito mínimo para que o cilindro desça o plano inclinado sem deslizar?
Dê suas respostas em termos de , ,,, . Dado: momento de inércia do cilindro .
Ver solução completaQuestão 23
Parte I:
Uma esfera sólida uniforme de massa e raio é colocada no lado de dentro de uma bacia hemisférica de raio . Existe atrito entre a esfera e a bacia. A esfera é liberada a partir do repouso fazendo um ângulo com a vertical, conforme ilustra a figura, e passa a rolar sem deslizar. A aceleração da gravidade é .
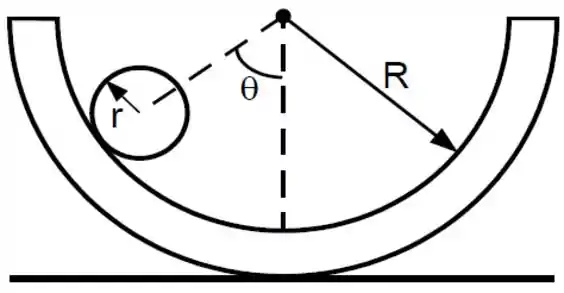
a) Expresse a conservação da energia do sistema.
b) Determine o módulo da velocidade angular da esfera quando ela atinge a parte inferior da bacia.
Parte II:
As setas no desenho abaixo, indicam as forças de atrito correspondentes à três posições da esfera quando ela está rolando sem deslizar no sentido horário. Assinale qual das opções é a verdadeira.
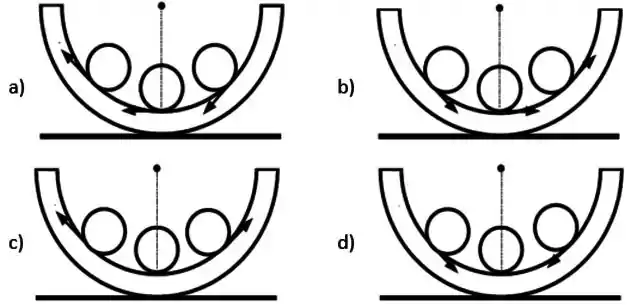
Questão 24
Considere o sistema abaixo, onde um cilindro maciço de massa e raio pode girar sem atrito em torno de um eixo vertical fixo à superfície, que passa pelo seu centro de massa. Uma corda ideal e de massa desprezível está enrolada em torno do cilindro, passa por uma polia em forma de aro com massa e raio e está presa a um bloco de massa desconhecida. Não há atrito nos eixos da rotação da polia e do cilindro e não ocorre escorregamento da corda no cilindro ou na polia. Tampouco há atrito entre o bloco e a superfície do plano inclinado. O raio da polia (aro) vale e o ângulo é . Observa-se que o bloco desce com uma aceleração linear .
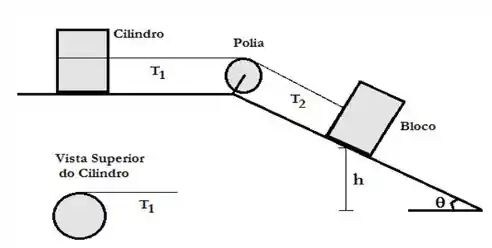
Havendo o sistema partido do repouso, observa-se que a polia sofre um deslocamento angular total de radianos até que o bloco chegue à base da rampa. Determine o tempo de queda do bloco, , e a velocidade angular final do cilindro maciço, .
Faça o diagrama do corpo livre para cada componente do sistema, representando claramente as forças que agem em cada um dos componentes e o sentido de seus movimentos (de translação ou rotação).
Escreva as equações resultantes das Leis de Newton (rotacional e translacional) para
os três corpos.
A partir das equações da letra , determine o valor da massa do bloco, em termos
de .
Ver solução completaQuestão 25
Um disco de raio e massa desce sem deslizar, a partir do repouso, a rampa inclinada conforme a figura. Após chegar à base da rampa , ele segue na horizontal para a pista em forma de circunferência com raio e sobe essa pista rolando sem deslizar. O ângulo entre a rampa e a horizontal é . O raio do disco vale e o comprimento da rampa, do ponto ao ponto , vale , onde é o raio da pista circular. A aceleração da gravidade local é . A linha tracejada corresponde a uma possível trajetória do centro de massa do disco.
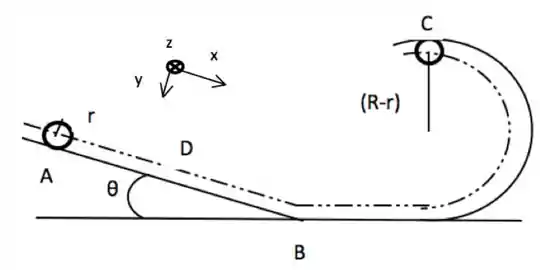
Faça o diagrama de forças para o disco durante o percurso de até . A partir das leis sobre torque e força, obtenha uma expressão literal, em função de , para o valor da aceleração do do disco entre e . Use o sistema de coordenadas desenhado na
figura.
Indique claramente o sentido da força de atrito estática feita pela superfície da rampa sobre o disco. Determine uma expressão literal para , em função de e . Resolva através da segunda lei de Newton aplicada ao centro de massa do disco.
Encontre uma expressão literal para o valor da velocidade angular do disco em
torno de um eixo horizontal que passe em seu , quando o disco chega ao ponto , em
função de e . Resolva através do uso de leis físicas referentes à energia mecânica.
O valor mínimo da velocidade do do disco para passar no ponto mais alto da
pista circular , sem perder o contato com a pista, é .
Obtenha uma expressão literal para a velocidade do do disco no ponto , , em
função de e através de leis físicas sobre a energia mecânica. Compare com o valor
mínimo dado e diga se o disco passará pelo ponto em contato com a pista ou se descolará dela antes de chegar a .
Ver solução completaQuestão 26
Um corpo rola sem deslizar ao longo de um plano inclinado de em relação à horizontal. Suponha que o corpo é uma esfera sólida. Para qualquer instante de tempo durante o rolamento no plano, calcule a razão entre a energia cinética de translação e a energia cinética total (
Ver solução completaQuestão 27
Um carretel é livre para girar em torno de um eixo fixo, e um cordão enrolado em torno do seu eixo faz com que ele gire no sentido anti-horário como indicado na . No entanto, se o carretel é colocado sobre uma mesa horizontal , com o ângulo entre o fio e a horizontal igual ao da , e se há força de atrito suficiente entre ele e a mesa, podemos dizer que tal carretel:
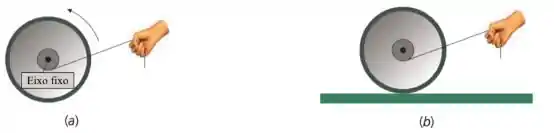

Questão 28
Uma corda ideal está enrolada em torno de um disco de raio . Ela pode desenrolar-se sem deslizar. O disco está montado num eixo sem atrito que passa pelo seu centro. Um bloco de massa está preso à extremidade livre da corda, conforme mostra a figura. Quando o sistema é liberado a partir do repouso observa-se que o bloco desce em . Responder justificando:
Qual o momento de inércia do disco?
Questão 30
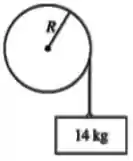
Um disco homogêneo de massa M e raio R encontra-se em repouso sobre uma superfície plana, horizontal e com atrito. Num dado instante, ele é puxado por um fio ideal que está enrolado em sua periferia, como mostrado na figura. A força exercida pelo fio e horizontal e tem módulo F constante. Sabe-se que o disco rola para a direita, sem deslizar sobre a superfície, e que seu momento de inércia em relação a um eixo perpendicular ao plano do disco e que passa pelo seu centro é .
- Faça um diagrama representando todas as forças que agem sobre o disco nos seus respectivos pontos de aplicação;
b) Calcule o módulo da aceleração do centro de massa do disco;
- Determine a força de atrito que age sobre o disco (módulo, direção e sentido).
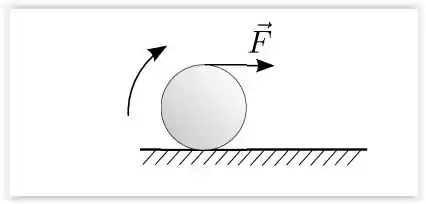
Questão 31
Um cilindro de massa rola sem deslizar sobre um plano horizontal rugoso com velocidade angular constante. O coeficiente de atrito estático entre o plano e o cilindro é . Seja o módulo da força de atrito estático entre o cilindro e a superfície, e , as energias cinética de rotação e translação do cilindro, respectivamente. Sabendo que o momento de inércia de um cilindro relativo ao seu eixo de simetria perpendicular às bases é , é correto afirmar que:
(a) e
(b) e
(c) e
(d) e
(e) e
(f) e
Ver solução completaQuestão 32
Uma esfera rígida homogênea de raio R rola sem deslizar sobre uma superfície horizontal com velocidade angular ω constante e velocidade do centro de massa . A figura mostra quatro pontos na superfície da esfera contidos no plano vertical da velocidade . Considere , , e os vetores velocidade dos pontos 1, 2, 3 e 4, respectivamente. A resposta correta é:
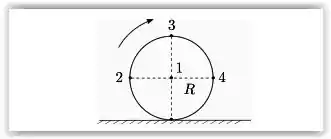
Questão 33
Uma roda, que pode ser considerada como um cilindro ideal, rola sem deslizar em uma superfície horizontal, com velocidade do seu centro de massa constante. Além da força peso, somente a superfície horizontal pode exercer forças sobre a roda. Pode-se afirmar, nesse caso, que a força de atrito que a superfície exerce sobre a roda é nula
a) A afirmativa é verdadeira
b) A afirmativa é falsa
Ver solução completaQuestão 34
Um cilindro maciço de comprimento L e raio R tem peso P. Duas cordas são enroladas em torno do cilindro, perto de cada borda, e as pontas das cordas são presas a ganchos no teto. O cilindro é mantido na horizontal com as duas cordas exatamente verticais e então é abandonado.
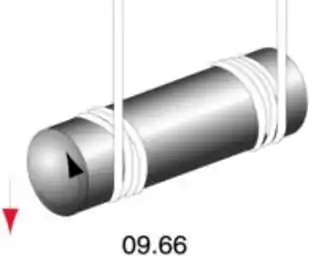
a) Faça o diagrama de forças sobre o cilindro.
b) Quais forças realizam trabalho durante a descida?
c) Calcule a tração em cada corda enquanto elas se desenrolam.
d) Calcule a aceleração linear do cilindro enquanto ele cai.
Ver solução completaQuestão 35
Um cilindro rígido e homogêneo de massa e raio está sobre uma superfície horizontal e pode girar livremente em torno de seu eixo de simetria longitudinal, como indicado na figura. O eixo está preso a uma extremidade de um fio ideal que passa por uma polia ideal e tem em sua outra extremidade um bloco suspenso de massa . O bloco desce verticalmente com aceleração para baixo e o cilindro rola sem deslizar sobre a superfície horizontal devido ao seu atrito com ela. O momento de inércia do cilindro relativo ao eixo de simetria é . Considere como dados e o módulo da aceleração da gravidade.
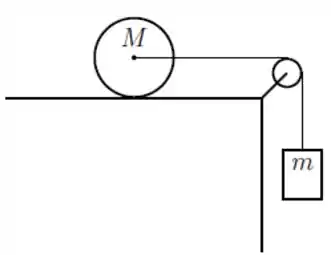
a) Indique todas as forças externas que atuam sobre o bloco e sobre o cilindro.
b) Calcule o módulo da aceleração do bloco;
c) Calcule o módulo da força de atrito sobre o cilindro e indique o seu sentido.
Ver solução completaQuestão 36
Uma esfera de bronze sólida de massa e raio rola sem deslizar ao longo de um plano inclinado após ser solta do repouso de uma altura . O momento de inércia da esfera em relação a um eixo que passa pelo seu centro que centro é e a aceleração da gravidade é . O plano inclinado forma um ângulo com a horizontal, como mostra a figura abaixo:
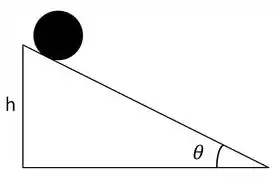
(a) Há atrito entre a esfera e o plano inclinado? Como você chegou a essa conclusão?
(b) Há conservação de energia mecânica? Justifique sua resposta levando em consideração o respondido no item (a).
(c) Utilizando considerações de energia, determine a velocidade com que a esfera atinge a base do plano inclinado.
(d) Obtenha a velocidade na base do plano inclinado já calculada no item (c) utilizando agora considerações de dinâmica (ou seja, aplicando a segunda lei de Newton).
Ver solução completaQuestão 37
Dois objetos A e B, ambos de seção circular de mesmo raio, rolam sem deslizar ao longo de umasuperfície inclinada, acelerando a medida que descem. Se o objeto A chega antes que o objeto B na base da superfície, é possível afirmar com certeza:
- a massa de A é maior que a de B.
- a massa de A é menor que a de B
- o momento de inércia de A é maior que o de B.
- o momento de inércia de A é menor que o de B
- Nenhuma das anteriores.
Dado: Momento de inércia de uma esfera de massa e raio cujo eixo de rotação passa pelo centro de massa da esfera:
Ver solução completaQuestão 38
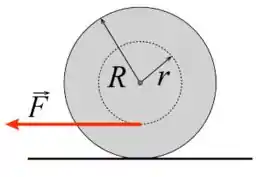
Um carretel de massa e raio externo rola sem deslizar, para a esquerda, ao ser puxado por uma força aplicada ao seu raio interno como mostra a figura. Sabe-se que o momento de inércia do carretel em relação ao seu centro de massa é .
- Qual a aceleração do centro de massa do carretel?
- Determine o módulo da força de atrito que atua no carretel e mostre que ela aponta para a direita.
- Se o coeficiente de atrito entre o carretel e a superfície é , qual a máxima força que pode ser aplicada ao carretel para que ele continue a rolar sem deslizar.
Questão 39
Um disco, um anel e uma esfera maciça de mesmo raio e massa descem rolando num plano inclinado, sem deslizar. É correto afirmar que:
Dados capa da prova: ; ;
(A) O disco chega primeiro na base do plano inclinado;
(B) O anel chega primeiro na base do plano inclinado;
(C) A esfera chega primeiro na base do plano inclinado;
(D) Chegaram juntos na base do plano inclinado;
(E) O disco chega antes que a esfera na base do plano inclinado;
Ver solução completaQuestão 40
. Uma roda de raio rola sem deslizar sobre uma pista horizontal. Partindo do repouso, a roda se move com aceleração angular constante de . A distância percorrida pelo
centro da roda desde até é:
Ver solução completaQuestão 41
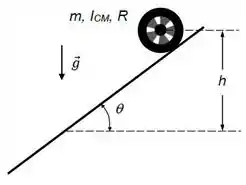
Uma roda possui massa , raio e momento de inércia em relação ao eixo perpendicular à sua superfície, passando pelo seu centro de massa (CM). Sabe-se que o CM da roda coincide com o seu centro. A roda rola sem deslizar sobre um plano inclinado de um ângulo com a horizontal (ver figura), onde e . Considere .
(A) Desenhe o diagrama de corpo isolado da roda, identificando cada força e o seu ponto de aplicação.
(B) Calcule a aceleração do CM da roda e a força de atrito que atua sobre ela.
(C) Calcule a velocidade do CM da roda após ela descer uma altura vertical ,
partindo do repouso.
(D) A força de atrito realiza trabalho ao longo dessa descida? Justifique sua resposta.
Questão 42
Uma casca esférica de massa e raio é abandonada em repouso na beirada de um hemisfério de raio , deslizando sem escorregar, como mostra a figura. Considere a aceleração gravitacional local . Quando a esfera passa pelo ponto mais baixo do hemisfério, calcule:
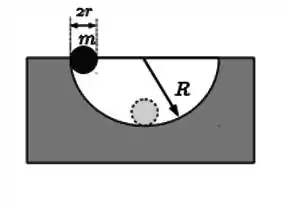
(a) Os módulos das velocidades angular da esfera e do centro de massa da esfera.
(b) A fração da energia cinética total correspondente à energia cinética de rotação.
(c) A forca exercida pela esfera sobre o hemisfério, expressa em termos de .
Dado: o momento de inércia de uma casca esférica de massa e raio em relação a um eixo que passa por um de seus diâmetros é .
Ver solução completaQuestão 43
Um anel fino de raio e massa é mantido verticalmente apoiado no solo e depois liberado. Suponha que a extremidade de apoio não escorregue. A aceleração gravitacional é . (Dado: momento de inércia de um anel fino de raio e massa em relação a um eixo que passa pelo seu centro de massa paralelo ao seu diâmetro é )
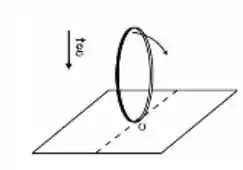
- Determine o momento de inércia do anel em relação ao ponto de apoio O.
- Determine a velocidade angular do anel imediatamente antes dele tocar o solo.
- Determine a velocidade da extremidade mais distante do ponto de apoio imediatamente antes dela tocar o solo.
Questão 44
Um balde pequeno de massa está preso a uma corda de massa desprezível que, por sua vez, encontra-se enrolada em torno de uma roldana cilíndrica de massa e raio como mostrado na figura. A roldana gira em torno de seu eixo de simetria. O balde é liberado a partir do repouso de uma altura do solo. No movimento que se segue, a corda se desenrola do cilindro sem deslizamento.
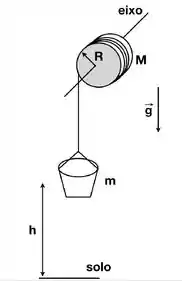
A. Adote um sistema de coordenadas, esboce o diagrama de forças para o balde e para a roldana e escreva todas as forças explicitamente no sistema de coordenadas adotado.
B. Baseado nas forças identificadas em (A), escreva as equações de movimento para o balde e para a roldana.
C. Determine o vetor aceleração do CM do balde. Calcule a magnitude dessa aceleração para os casos extremos em que e .
D. Determine a velocidade com que o CM do balde atinje o chão. Considere o balde como uma partícula pontual.
E. Verifique explicitamente a validade do teorema do trabalho-energia cinética para o sistema “balde+roldana+corda”.
Ver solução completaQuestão 45
Um disco homogêneo de massa e raio pode girar livremente em torno de um eixo perpendicular a ele que passa pelo seu CM, cujo momento de inércia é . O disco parte do repouso e inicia uma subida sobre a rampa, ao ter seu eixo puxado por uma força constante de módulo , paralela à superfície da rampa, como indica a figura. A superfície da rampa está inclinada de um ângulo com a horizontal e o disco rola sem deslizar ao subir por essa superfície. Nas questões abaixo indique claramente os conceitos utilizados.
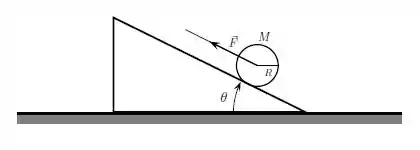
a) Faça um diagrama indicando as forças que atuam no disco.
b) Determine o módulo da aceleração do centro de massa, , do disco.
c) Determine o tempo que ele leva para completar a primeira volta em torno do seu eixo em função de e dos dados do problema.
d) Determine o trabalho realizado por cada uma das forças indicadas no item (a) na primeira volta completa em torno de seu eixo, justificando cada uma delas.
Ver solução completaQuestão 46
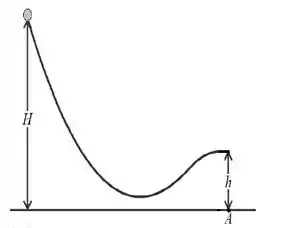
Na figura abaixo, uma pequena bola maciça de massa e raio rola sem deslizar, a partir do repouso, de uma altura até deixar a parte horizontal no fim da pista a uma altura do solo. Desprezando a resistência do ar, a que distância horizontal do ponto a bola atinge o solo?
Dados:
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 47
Um anel e um disco de mesma massa e mesmo raio rolam sem deslizar por uma rampa de altura significativamente maior que seus raios, partindo simultaneamente da mesma altura. Avalie as afirmações abaixo em relação à sua veracidade:
- Ao final da rampa a energia cinética de rotação do anel é maior do que a do disco.
- A energia mecânica total do sistema não se conserva por haver uma força de atrito agindo.
- Por haver um momento de inércia menor, o disco chega primeiro ao final da rampa.
São corretas as afirmações:
a) todas as afirmações
b) nenhuma das afirmações
c) I e II
d) I e III
e) II e III
Ver solução completaQuestão 48
A figura abaixo mostra um ioiô na forma de um disco homogêneo de raio R e massa M. Quando o ioiô é liberado do repouso no instante t = 0, o fio ideal ao seu redor desenrola sem deslizar. O ioiô então executa um movimento vertical descendente com rotação ao redor do eixo perpendicular à sua superf ́ıcie e passando no seu centro de massa (CM).
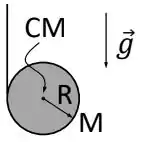
a) Desenhe o diagrama de corpo isolado do ioiô, identificando cada força e o seu ponto de aplicação.
B) Calcule a aceleração do CM do ioiô. Deixe sua resposta em função apenas da aceleração da gravidade g.
Dado: Momento de inércia de um disco homogêneo de raio R e massa M ao redor do eixo perpendicular a sua superfície e passando no seu CM:
C) Calcule a velocidade angular do ioiô no instante t. Deixe sua resposta em função apenas de t, R e g.
Ver solução completaQuestão 49
Um disco homogêneo de massa e raio está enrolado a um fio ideal que está preso ao teto e é solto a partir do repouso, no instante . O fio não desliza sobre a extremidade do disco, conforme mostra a figura.
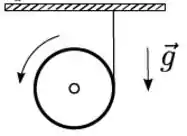
Sabendo que o momento de inércia do disco, em relação ao eixo perpendicular a ele que passa pelo seu centro de massa, é , podemos afirmar que:
(a) O centro de massa do disco desce com aceleração de módulo .
(b) O centro de massa do disco desce com aceleração de módulo .
(c) Enquanto o disco desce, a tração no fio é .
(d) O centro de massa do disco desce com aceleração de módulo .
(e) O centro de massa do disco desce com aceleração de módulo .
(f) Enquanto o disco desce, a tração no fio é .
(g) Enquanto o disco desce, a tração no fio é .
Ver solução completaQuestão 50
Uma bola de sinuca de raio rola sem deslizar do topo de um domo esférico com raio , onde . Considere que a velocidade inicial da bola de sinuca de raio é desprezível. Encontre o módulo da velocidade angular da bola de sinuca no momento em que ela perde contato com o domo.
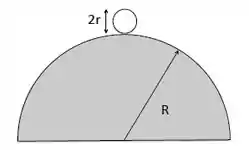
Formulário: Momento de inércia da esfera .
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 51
O disco mostrado na figura tem massa e raio e está sendo puxado por uma força horizontal aplicada em seu centro de massa. Ele rola sem deslizar sobre uma superfície horizontal áspera. O coeficiente de atrito estático entre o disco e a superfície é . Obtenha os resultados em função dos dados fornecidos.
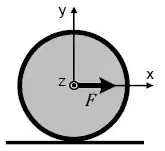
a) Faça o diagrama de forças sobre o disco. Determine uma expressão literal para o módulo da aceleração angular 𝛼 do disco. Faça o mesmo para o módulo e o sentido da força de atrito .
Ver solução completaQuestão 52
Uma roda homogênea de massa e raio encontra-se inicialmente em repouso sobre uma superfície horizontal (ver figura abaixo). O plano da roda é vertical. A partir de um instante de tempo aplica-se uma força horizontal constante de módulo no seu centro, e a roda passa a girar sem deslizar.
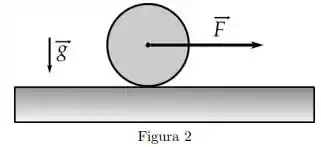
Sabe-se que o momento de inércia da roda em relação ao seu eixo de rotação é . Denotando a aceleração do seu centro de massa por , pode-se afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
Ver solução completaQuestão 53
Uma esfera maciça em repouso está sobre um plano inclinado e possui uma fita ideal enrolada em torno de sua periferia vertical. Essa fita passa em polia ideal e está ligada a um bloco. Veja figura. Após liberar o conjunto, a esfera sobe o plano sem deslizar e o bloco desce.
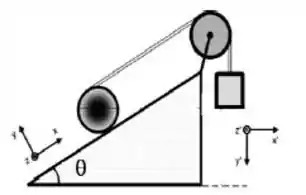
Encontre uma expressão literal para o módulo da aceleração do CM da esfera e da aceleração do bloco. São dados o raio da esfera 𝑅, o ângulo 𝜃, as massas da esfera 𝑀 e do bloco 𝑚 e a aceleração da gravidade 𝑔. A aceleração da fita no ponto superior da esfera é duas vezes a aceleração do CM da esfera.
Dados: Esfera:
(a) Escreva a equação do movimento para o bloco acompanhada do respectivo diagrama de corpo livre.
(b) Escreva a equação do movimento de translação da esfera acompanhada do respectivo diagrama de corpo livre. Faça o mesmo para a equação do movimento de rotação da esfera. Escreva também a condição de rolamento sem deslizamento.
(c) Resolva o sistema de equações e encontre uma expressão literal para o módulo da aceleração do CM da esfera em função dos dados fornecidos.
Ver solução completaQuestão 54
Dois discos A e B têm o mesmo momento de inércia, e estão em rotação com aceleração angular diferente de zero, conectados por uma correia que passa por suas periferias e não desliza sobre os discos. Os raios dos discos são e , respectivamente, conforme mostrado na figura.
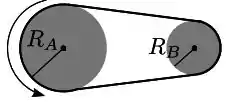
Comparando dois pontos situados na periferia de cada disco para um determinado instante, qual a única das quantidades abaixo que é a mesma?
(a) Módulo da velocidade linear.
(b) Módulo da aceleração angular.
(c) Módulo da velocidade angular.
(d) Módulo da aceleração linear.
(e) Componente radial da aceleração.
Ver solução completaQuestão 55
Considere um automóvel com tração dianteira. Quando o carro acelera, em que sentido aponta a força de atrito, , na roda dianteira e, , na roda traseira, respectivamente?
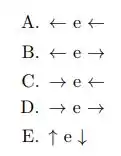
Questão 56
Um cilindro homogêneo de massa e raio sobe um plano inclinado de um ângulo em relação à horizontal sob a ação de uma força constante, como mostra a figura abaixo. O cilindro parte do repouso e sua velocidade angular aumenta com o tempo. Sabe-se que o cilindro rola sem deslizar e que seu momento de inércia em relação a um eixo perpendicular que passa pelo seu centro de massa é .
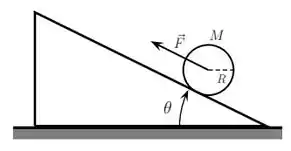
a) No rolamento sem deslizamento de um corpo rígido de raio , a relação entre os módulos da aceleração do centro de massa de um corpo rígido e a aceleração angular do corpo em relação ao centro de massa é . Justifique essa relação.
Ver solução completaQuestão 57
Um cilindro homogêneo de massa e raio sobe um plano inclinado de um ângulo em relação à horizontal sob a ação de uma força constante, como mostra a figura abaixo. O cilindro parte do repouso e sua velocidade angular aumenta com o tempo. Sabe-se que o cilindro rola sem deslizar e que seu momento de inércia em relação a um eixo perpendicular que passa pelo seu centro de massa é .
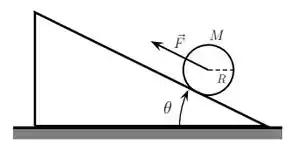
Dado:
b) Determine a força de atrito (módulo, direção e sentido) que o plano excerce sobre o cilindro.
c) Determine a velocidade do centro de massa do cilindro após o mesmo ter subido uma altura h, em relação à sua posição inicial.
Ver solução completaQuestão 58
Dois discos idênticos e , ambos com momento de inércia rolam sem deslizar ao longo de uma superfície horizontal com a mesma velocidade. Em um dado momento, esta superfície inclina-se para cima. O disco continua o movimento de rolamento e sobe a superfície inclinada sem deslizar. Por outro lado, o disco não sofre nenhum atrito durante a sua subida sobre a superfície inclinada. O disco atinge uma altura de antes de rolar para baixo novamente. A altura atingida pelo disco é:
a)
b)
c)
d)
e)
Ver solução completaQuestão 59
Um corpo rola sem deslizar ao longo de um plano inclinado de em relação à horizontal. Suponha desconhecida a geometria do corpo. Mede-se que a aceleração do centro d emassa durante a descida é . Supondo que o momento de inércia do corpo tem a forma , calcule o valor de .
Ver solução completaQuestão 60
A figura ,que se refere às Questões 1, 2 e 3, representa um aro que rola sem deslizar sobre uma superfície horizontal.
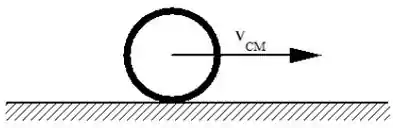
Suponha que a massa do aro seja e a velocidade do centro de massa seja . Dado que , onde é o raio do aro, a energia cinética do aro é
(A) J
(B) J
(C) J
(D) J
(E) J
Ver solução completaQuestão 61
Um corpo homogêneo, de seção reta circular de raio , é liberado do repouso e rola sem deslizar sobre um plano inclinado. O gráfico da velocidade do centro de massa do corpo em função do tempo é mostrado na Figura 2
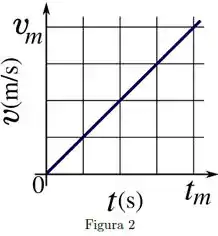
onde e . Qual é a aceleração angular do corpo?
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 62
Uma esfera desce um plano inclinado de um ângulo em relação à direção horizontal, rolando sem deslizar, sujeita à ação apenas das forças peso, normal e atrito. É correto afirmar que:
(a) Apenas a força de atrito exerce torque em relação ao centro de massa da esfera.
(b) Apenas a força peso exerce torque em relação ao centro de massa da esfera.
(c) As forças peso e atrito exercem trabalho diferente de zero sobre a esfera.
(d) A força normal não exerce torque em relação ao centro de massa pois atua no centro de massa da esfera.
(e) O centro de massa da esfera desce a rampa com aceleração constante igual a .
(f) Os trabalhos realizados pelas forças normal e de atrito se cancelam.
Ver solução completaQuestão 63
Um disco sólido de massa , raio e momento de inércia , rola sem deslizar ao longo de uma superfície com velocidade constante e velocidade angular . Qual é o momento angular do disco com relação ao seu prórpio eixo, enquanto ele rola?
(A) ;
(B) ;
(C) ;
(D) ;
(E) ;
Ver solução completaQuestão 65
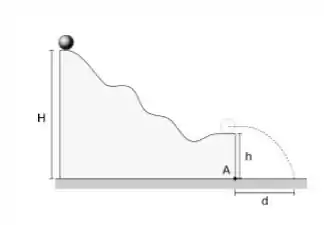
Uma bola maciça rola suavemente (sem deslizar) a partir do repouso, começando de uma altura , até deixar a parte horizontal no fim da pista, a uma altura , conforme a figura ao lado. Dado que o momento de inércia de uma bola maciça de massa M e raio em relação ao centro de massa é e , responda:
(a) Qual a velocidade do centro de massa da partícula no fim da pista?
(b) Usando a resposta do item anterior, calcule a que distância horizontal do ponto a bola toca o chão.
Questão 66
Considere uma esfera que rola sem deslizar sobre uma calha simétrica que tem dois trechos retilíneos, I e II, como mostra a figura. Ela oscila descendo e subindo nos dois ramos da calha. No trecho I a força de atrito é e no trecho II, é . Considere que as únicas forças que atuam sobre a esfera sejam a força normal e a força de atrito exercidas pela calha, e o seu peso.
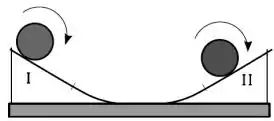
Dentre os diagramas seguintes:
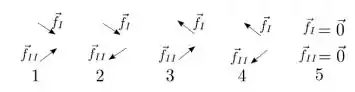
o que melhor representa o sentido e a direção das forças de atrito e nos trechos I e II é:
- 3
- 1
- 2
- 4
- 5
- Nenhuma das alternativas
Questão 67
Considere um carretel ou ioiô, isto é, um cilindro com rebordo usado para enrolar um fio. O fio é puxado lentamente por uma força , fazendo com que o carretel passe a rolar sem deslizar em uma superfície horizontal. O fio é puxado nas duas situações ilustradas nas figuras ao lado. Em ambos os casos, o atrito não pode ser desprezado.
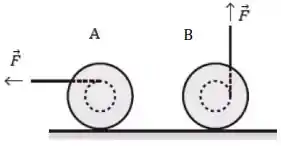
Julgue as afirmações abaixo:
(I) Nos casos A e B, o carretel gira no sentido anti-horário.
(II) Nos casos A e B, o centro de massa do carretel se move para a esquerda.
(III) No caso B, o centro de massa do carretel permanece parado, pois não há forças na direção horizontal.
Qual opção abaixo contém todas as afirmações que estão corretas?
(A)
(B)
(C)
(D) e
(E) e
Ver solução completaQuestão 68
Um caixote é transportado numa plataforma horizontal apoiada sobre cilindros de raio . A plataforma se move para a direita com velocidade sem deslizar sobre os cilindros que rolam sem deslizar sobre a superfície horizontal. O módulo da velocidade angular de cada cilindro em relação ao seu centro de massa é
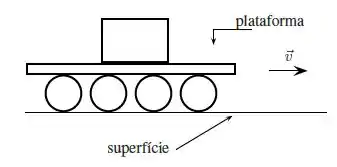
a)
b)
c)
d)
e)
Ver solução completaQuestão 69
Um cilindro de raio e massa é puxado por uma força horizontal de módulo em uma superfície também horizontal, por onde rola, sem deslizar. Sabendo que os coeficientes de atrito estático e cinético entre o cilindro e a superfície são, respectivamente, e ,
qual o trabalho realizado pela força de atrito em uma volta completa do cilindro?
Questão 70
Considere um carretel de raio externo , massa e momento de inércia em relação ao centro de massa . Ele está em repouso quando uma corda enrolada no cilindro interno de raio é puxada com uma força de tração horizontal constante . O carretel passa a rolar sem deslizar no sentido horário (para a direita) em um plano horizontal com coeficiente de atrito estático . As forças na direção horizontal, atrito e tração, agindo no carretel estão ilustradas na figura.
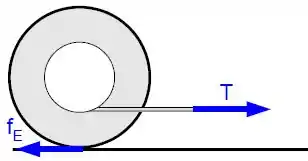
a) Escreva as equações de movimento que descrevem a dinâmica do carretel como translação do centro de massa e rotação em torno do centro de massa.
b) Use as equações do item anterior para obter o modulo da aceleração angular α em relação ao centro de massa do carretel.
c) Qual é o valor máximo da tração para o rolamento sem deslizamento.
Ver solução completaQuestão 71
Considere o modelo simplificado de um carro descrito pela figura 1, que possui apenas duas rodas: uma traseira e uma dianteira. A distância entre as duas rodas é dada por . O centro de massa do carro se encontra no ponto de distância de distância da roda traseira. .
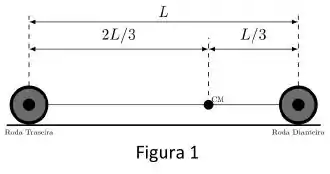
De agora em diante considere que ambas as rodas possuem raio , massa e momento de inércia ao redor do centro de massa . No item (b) existe atrito entre as rodas e o chão, e elas rolam sem deslizar.
b) A figura 2 descreve uma versão simplificada da roda dianteira em movimento. O motor realiza sobre ela um torque (para dentro da folha). A força (SI) é a força que o veículo faz sobre a roda, que é aplicada diretamente no centro de massa da roda. Calcule a aceleração angular da roda. Cuidado ao escolher a direção da força de atrito.
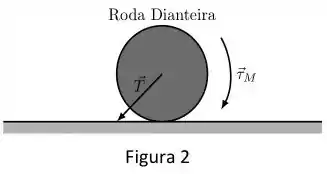
Questão 72
Uma bolinha compacta de massa m e raio r rola sem deslizar ao longo do trilho em curva mostrado na figura abaixo, tendo sido abandonado em repouso em algum ponto da região reta do trilho.
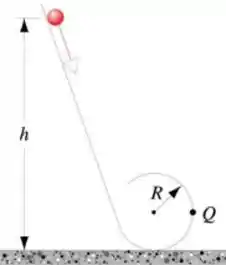
a) De que altura mínima h, a partir da base do trilho, a bolinha deve ser solta para eu percorra a parte superior da curva? (suponha que R>>r).
b) Se a bolinha for solta da altura 6R acima da base do trilho, qual a componente horizontal da força que atua sobre ela no ponto Q?
Ver solução completaQuestão 73
A figura ,que se refere às Questões 1, 2 e 3, representa um aro que rola sem deslizar sobre uma superfície horizontal.
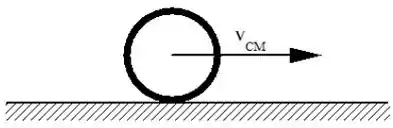
O ponto com maior rapidez em relação à superfície é
(A) o ponto de contato do aro com a superfície.
(B) o ponto no centro do aro.
(C) o ponto no topo do aro, oposto ao ponto de contato com a superfície.
(D) o ponto mais à frente do aro, na altura do seu centro de massa.
(E) o ponto mais atrás do aro, na altura do seu centro de massa.
Ver solução completaQuestão 74
Uma bola de basquete (massa M = 600g e raio R= 12,0cm) sobe um plano inclinado (θ = 30) rolando sem deslizar. Na base do plano, o topo da esfera tem velocidade v = 5,00m/s.
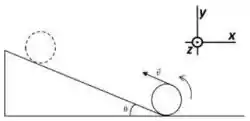
- Faça um diagrama de corpo livre que represente a bola num ponto qualquer do plano inclinado.
- Calcule o módulo do torque resultante () sobre a bola e forneça sua direção e sentido em termos dos vetores unitários de acordo com o sistema de coordenadas da figura.
Questão 75
Uma roda de massa , raio e momento de inércia em relação ao seu eixo de simetria, tem seu eixo ligado a uma mola ideal de constante , preso a uma parede. A roda gira sem deslizar sobre um piso com atrito estático . é a posição dp centro de massa com relação ao ponto de equilíbrio.
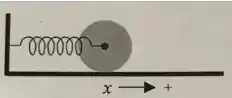
(a) Para um movimento para a direita (valores positivos de ), qual direção da aceleração do centro de massa? A direção da aceleração angular em relação ao centro de massa (horário ou anti-horário)? A direção do atrito estático, ? E a direção do torque, ?
(b) Encontre a força de atrito , em função de e .
(c) Encontr a força resultante em função de e .
Ver solução completaQuestão 76
. Quando a velocidade de um carro de tração traseira está aumentando sobre uma pista horizontal, o sentido da força de atrito sobre os pneus é:
para a frente em todos o pneus;
para trás em todos o pneus;
para trás nos pneus dianteiros e para a frente nos pneus traseiros;
zero;
para a frente nos pneus dianteiros e para trás nos pneus traseiros;
Ver solução completaQuestão 77
Considere uma esfera que rola sem deslizar sobre uma calha simétrica que tem dois trechos retilíneos, e , como mostrado na figura. Ela oscila descendo e subindo nos dois ramos da calha. No trecho a força de atrito é e no trecho , é . Considere que as únicas forças que atuam sobre a esfera sejam a força normal e a força de atrito exercidas pela calha, e seu peso.
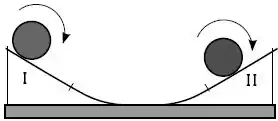
Dentre os diagramas seguintes

O que melhor representa o sentido e a direção das forças de atrito e nos trechos e é
- ;
- ;
- ;
- ;
- ;
Questão 78
Uma roda homogênea de massa e raio encontra-se inicialmente em repouso sobre uma superfície horizontal (ver figura abaixo). O plano da roda é vertical. A partir de um instante de tempo aplica-se uma força horizontal constante de módulo no seu centro, e a roda passa a girar sem deslizar.
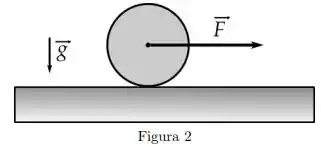
Nesse caso, a força de atrito entre a roda e a superfície:
é nula e a energia total da roda é conservada.
é diferente de zero e a energia total da roda não é conservada.
é diferente de zero e a energia total da roda é conservada.
é diferente de zero e é estática.
é diferente de zero e é cinética.
é igual ao coeficiente de atrito multiplicado pelo módulo da força normal.
Estão corretas somente as afirmações:
(a)
(b) e
(c) , e
(d) e
(e) , e
(f) e
(g) , e
(h) e
(i) , e
Ver solução completaQuestão 79
Três objetos são liberados do repouso e rolam sem deslizar sobre um plano inclinado, que faz um ângulo com a horizontal. Os três objetos possuem a mesma massa e raio , e possuem respectivamente momentos de inércia , e e acelerações , , e . O que se pode afirmar sobre os módulos das acelerações?
(a)
(b)
(c)
(d)
(e)
(f)
(g) Não é possível determinar
Ver solução completaQuestão 80
Sobre um rolamento sem deslizamento de um cilindro sobre o chão, é correto dizer que:
A. a velocidade do centro de massa é independente da velocidade angular;
B. a velocidade escalar do ponto mais alto do cilindro é menor que a velocidade do centro de massa;
C. a velocidade escalar do ponto mais alto do cilindro é maior que a velocidade do centro de massa;
D. a velocidade escalar do ponto mais alto do cilindro é igual à velocidade do centro de massa;
E. a velocidade do ponto de contato com o chão é vezes a velocidade do centro de massa.
Ver solução completaQuestão 81
5) Uma molécula tri-atômica linear é formada por dois átomos laterais idênticos A de massa ligados a um átomo central B de massa . Essa molécula apresenta, no caso geral, um movimento de rotação superposto a um movimento de vibração linear em que os dois átomos laterais se aproximam e se afastam simultaneamente do átomo central, como se estivessem presos por duas molas. Se em um dado instante, quando a distância entre os átomos laterais é , o módulo da velocidade angular da molécula é , então o módulo dessa velocidade angular quando a distância mudar para será:
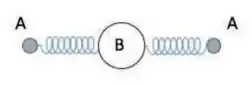
(a)
(b)
(c)
(d)
e)
Ver solução completaQuestão 82
A figura a seguir mostra um objeto uniforme que rola sem deslizar sobre um plano inclinado. O objeto possui massa , raio e momento de inércia ao redor do eixo de rotação. Sabe-se que quando o objeto é liberado do repouso a partir de uma certa altura , ele é lançado horizontalmente ao chegar à base do plano inclinado, tocando o solo a uma distância horizontal do ponto de lançamento.
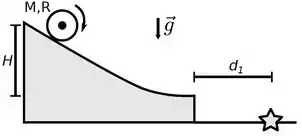
Considere, agora, que o objeto é substituído por outro, de mesma massa , mesmo raio e momento de inércia () ao redor do eixo de rotação. Nesse caso, quando solto do repouso da mesma altura , o novo objeto rola sem deslizar, e toca o solo a uma distância do ponto de lançamento.
Pode-se afirmar que:
Questão 83
A figura mostra um disco homogêneo de raio rolando para baixo sem deslizar, com velocidade angular variável, em uma rampa inclinada em um ângulo . As forças que estão atuando nele são as forças peso , a força normal e a força de atrito . O ponto está no centro de massa do disco. É possível afirmar que:
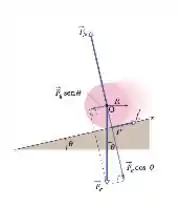
- Nenhuma das forças mostradas realiza torque em relação ao ponto O.
- A energia cinética do disco é puramente translacional.
- A energia cinética total do disco é dada por , onde é seu momento de inércia em relação ao eixo que passa pelo ponto perpendicularmente ao plano do disco.
- A velocidade linear do ponto do disco em contato com o plano (ponto P na figura) é
- O torque resultante em relação ao ponto é não nulo e é realizado apenas por .
- A condição de rolamento sem deslizamento é que o torque resultante em relação ao ponto O seja nulo.
- A condição de rolamento sem deslizamento é que a aceleração do ponto O seja .
Questão 84
Um disco de massa rola sem deslizar, com velocidade angular constante, sobre uma superfície horizontal, mantendo-se sempre alinhado verticalmente. Nos diagramas abaixo, , , e , aquele que presenta corretamente os vetores velocidade (indicados por setas) dos pontos e , da periferia do disco e o seu centro, em relação a um observador parado na Terra é
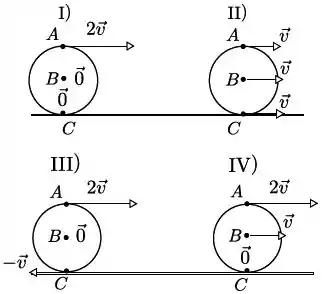
- nenhum deles
Questão 85
Uma esfera de raio experimenta rolamento sem deslizamento num plano inclinado que forma um ângulo com a horizontal. Durante um percurso de descida, se o momento de inércia é a aceleração será:
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 86
Uma bola de boliche rola sem deslizar com velocidade sobre uma esteira rolante que se desloca no sentido contrário com a mesma velocidade, de forma que a bola não se desloca em relação ao chão. Calcule a energia cinética da bola de boliche em relação ao chão:
- .
- .
- .
- Zero
Dado: Momento de inércia de uma esfera maciça:
Ver solução completaQuestão 87
Uma esfera maciça homogênea rola sem deslizar ao longo de uma superfície horizontal. Que percentagem da sua energia cinética total está sob a forma de energia cinética rotacional? O momento de inércia de uma esfera maciça homogênea em relação a um eixo que passa pelo seu centro é
(A) 33 % (B) 50 % (C) 12 % (D) 75 % (E) 29 %
Ver solução completaQuestão 88
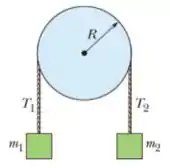
18) Na figura abaixo, o bloco tem massa , o bloco tem massa , e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio . Quando o sistema é liberado a partir do repouso o bloco cai em sem que a corda deslize na borda da polia. (a) Qual é o módulo da aceleração dos blocos?
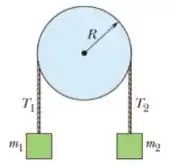
Questão 89
18) Na figura abaixo, o bloco tem massa , o bloco tem massa , e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio . Quando o sistema é liberado a partir do repouso o bloco cai em sem que a corda deslize na borda da polia. Qual é o valor (b) da tensão .
Questão 90
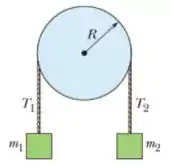
18) Na figura abaixo, o bloco tem massa , o bloco tem massa , e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio . Quando o sistema é liberado a partir do repouso o bloco cai em sem que a corda deslize na borda da polia. Qual é o valor (c) da tensão ?
Questão 92
Um cilindro maciço de massa e raio desce rolando sem deslizar sobre um plano inclinado de em relação à horizontal. O cilindro parte do repouso e percorre uma distância no plano inclinado. Qual é a velocidade de seu centro de massa no final da distância ? (Dado: .)
(A)
(B)
(C)
(D)
(E)
Ver solução completaQuestão 94
Uma esfera sólida de massa e raio rola sem deslizamento ao longo da trajetória mostrada na figura. Ela inicia o movimento partindo do repouso quando a esfera está a uma altura acima da parte inferior do loop de raio , muito maior do que .
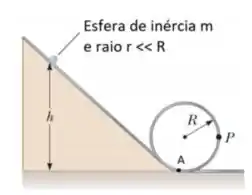
a) Qual o módulo da velocidade quando a esfera chega no ponto A?
b) Qual o módulo da velocidade angular na base, ponto A, do plano inclinado?
c) Desenhe o diagrama de corpo livre da esfera quando esta estiver no ponto P.
d) Qual é o valor mínimo de (em termos de ) para que a esfera complete o loop?
Ver solução completaQuestão 95
Quando nós aplicamos o princípio da conservação da energia a um cilindro que rola sem deslizar para baixo em um plano inclinado, nós excluímos o trabalho realizado pelo atrito porque:
a velocidade linear do ponto de contato (relativamente ao plano inclinado) é zero;
os coeficientes de atrito estático e cinético são iguais;
não há atrito presente;
coeficiente de atrito cinético é zero;
a velocidade angular do centro de massa em torno do ponto de contato é zero;
Ver solução completaQuestão 96
Dois cilindros rígidos homogêneos, A e B, rolam sem deslizar sobre uma superfície horizontal, com a mesma velocidade angular constante de módulo ω. As relações entre as massas e os raios dos cilindros são e e. O momento de inércia de um cilindro homogêneo de massa M e raio R relativo ao seu eixo, que passa pelo centro de massa, é . Sendo e a energia cinética total e o módulo da velocidade do centro de massa do cilindro A, e e as do cilindro B, podemos dizer que:
Questão 97
Uma roda de massa e raio rola sem deslizar sobre uma superfície horizontal com
atrito ao ser puxada por uma força, aplicada sobreo seu eixo. O coeficiente de atrito entre a roda e a superfície é , e a velocidade do centro de massa é. O momento de inércia total da roda éem torno do eixo que passa pelo seu centro de massa.
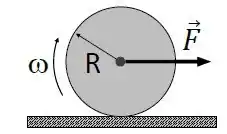
Julgue as seguintes assertivas
I. Na ausência de deslizamento, .
II. A energia cinética total da roda é.
III. Quando a força , é constante e a força de atrito é nula.
É correto apenas o que se afirma em
(A) I
(B) II
(C) III
(D) I e II
(E) I e III
(F) II e III
(G) Todas
(H) Nenhuma
Ver solução completaQuestão 98
Seja um cilindro maciço e homogêneo, de raio e massa , (cilindro 1) que pode girar sem atrito em torno de um eixo vertical que passa pelo seu centro. O eixo está fixado em uma mesa horizontal, sobre a qual se encontra o cilindro. Enrolada na superfície curva do cilindro há uma corda inextensível, que passa por uma roldana e tem na extremidade livre um outro cilindro (cilindro 2) de massa que cai sob a ação da gravidade. As massas da roldana e da corda são desprezíveis e a corda não desliza.
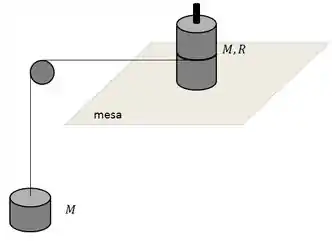
a) Nestas condições, escreva as equações de movimento do cilindro 1 e do cilindro 2
(isto é, escreva as equações que relacionam as forças existentes com as acelerações) e
calcule a tensão na corda.
Ver solução completaQuestão 99
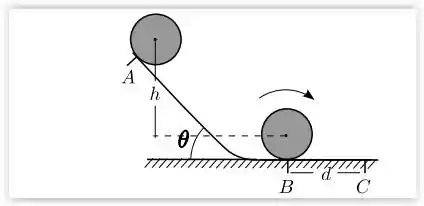
A figura mostra uma rampa constituída por um trecho plano, inclinado de um angulo em relação à horizontal, que se conecta suavemente a um trecho plano horizontal. Um cilindro homogêneo de massa e raio é liberado a partir do repouso em um ponto A do plano inclinado e desce percorrendo a rampa passando pelos pontos B e C do trecho horizontal, rolando sem deslizar durante todo o trajeto; de A para B o centro de massa desce uma altura . Lembrando que o momento de inércia do cilindro relativo ao seu eixo de simetria perpendicular às bases , calcule:
a) a aceleração do centro de massa do cilindro, enquanto ele desce o plano inclinado;
b) a força de atrito (modulo, direção e sentido) que age no cilindro enquanto ele desce o plano inclinado;
c) a velocidade do centro de massa do cilindro ao passar pelo ponto B;
d) o trabalho realizado por cada uma das forças que agem sobre o cilindro, quando seu centro de massa se desloca de uma distância entre os pontos B e C.
Questão 100
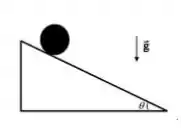
Uma esfera homogênea de massa e raio , inicialmente em repouso, rola sem deslizar sobre um plano inclinado que forma um ângulo com a horizontal (ver figura). O momento de inércia da esfera ao redor do seu centro de massa é . A aceleração gravitacional é .
(a) Desenhe todas as forças atuando na esfera, indicando o seu ponto de aplicação.
(b) Calcule a força de atrito entre a esfera e o plano inclinado.
(c) Suponha, agora, que a esfera esteja rolando na iminência de deslizar. Determine o coeficiente de atrito estático entre a esfera e o plano inclinado.
Questão 101
Um aro de massa e raio é abandonado do repouso no topo de um plano inclinado simultaneamente com outro aro de massa e raio . Os aros rolam sem deslizamento. Qual aro chega primeiro à base do plano inclinado? Dado:
(A) O aro com massa maior.
(B) O aro com massa menor.
(C) O aro com maior momento de inércia.
(D) O aro com menor momento de inércia.
(E) Ambos chegam juntos.
Ver solução completaQuestão 102
Uma esfera de massa 400 g e raio 4 cm é liberada, a partir do repouso, do topo de uma rampa inclinada de 25º com relação à horizontal. A rampa tem comprimento de 2.1 m. A esfera rola sem deslizar até o fim da rampa.
a) Qual é a velocidade angular da esfera no final da rampa?
b) Qual fração da energia cinética da esfera é rotacional?
Ver solução completaQuestão 103
Um aro circular de 60 cm de diâmetro está rolando sem deslizar sobre uma superfície plana. O módulo da velocidade do seu centro de massa é de 20 m/s. Qual o módulo da velocidade do ponto na extremidade frontal do aro?
Ver solução completaQuestão 104
Uma esfera rígida homogênea de raio rola sem deslizar sobre uma superfície horizontal com velocidade angular constante e velocidade do centro de massa . A figura mostra quatro pontos na superfície da esfera contidos no plano vertical da velocidade . Considere , , e os vetores velocidade dos pontos 1, 2, 3 e 4, respectivamente.
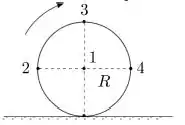
A resposta correta é:
(a)
(b)
(c)
(d)
(e)
(f)
Ver solução completaQuestão 105
Uma roda homogênea é constituída por um disco maciço, uniforme, de massa , com um orifício de raio externo e raio interno . Há um eixo encaixado nele rigidamente (veja a figura).
O eixo que passa pelo orifício é cilíndrico, maciço, homogêneo, tem raio e a mesma massa . O momento de inércia do conjunto roda-eixo em relação ao centro de massa do eixo é . A roda está inicialmente em repouso no alto de uma rampa que faz um ângulo , pequeno, com a horizontal. Essa rampa possui um sulco aberto e largo no qual a roda se encaixa, sem tocá-la. O eixo está apoiado na rampa.
Após ser liberada, a roda rola suavemente, sem deslizamento, para baixo com seu centro de massa descendo uma distância .
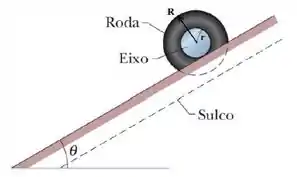
- Determine uma expressão literal para o valor da velocidade angular da roda no final da distância , em função dos dados citados. Sugestão: faça por energia.
- Determine uma expressão literal para o valor da força de atrito estático sobre da roda durante a descida em função dos dados citados.
Questão 106
Um disco é liberado a partir do repouso do alto de uma superfície inclinada de altura (medida desde o solo até o ponto mais baixo do disco como mostrado na figura) e rola suavemente sem deslizar até a parte mais baixa da superfície. No primeiro trecho, a superfície é retilínea e forma um ângulo com a horizontal, como mostrado na figura. Dados: o momento de inércia do disco homogêneo com relação a um eixo que passa pelo centro de massa é , onde é a massa do disco e é seu raio. Considere .
(a) Calcule a aceleração do centro de massa do disco quando ele ainda se encontra no trecho retilíneo na superfície.
(b) Determine a velocidade do centro de massa quando o disco atinge a parte mais baixa da trajetória.