Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 18.1 - Ex. 55
Neste problema, 1,00 mol de um gás ideal é aquecido enquanto seu volume varia de forma que onde A é uma constante. A temperatura varia de até . Determine o trabalho realizado sobre o gás.
Passo 1
Muito bem, queremos o trabalho, mas como? Nós não temos praticamente nada para calculá-lo, certo? Então como faremos?
Precisamos lembrar que o trabalho é calculado como a área abaixo da curva PV formada. Ou seja, a área abaixo da linha ligando o estado inicial e final.
Legal, então vamos fazer um diagrama PV ! Mas como? Vamos precisar do estado inicial e final. Algumas informações nós possuímos.
No estado inicial:
Jogando na fórmula da temperatura:
Já sabemos agora precisamos do volume inicial. Aqui podemos usar uma relação muito conhecida para os gases:
O problema nos disse que e
Na pressão inicial:
Chegamos às coordenadas para o estado inicial: ().
Passo 2
Agora vamos passar para o estado final:
Jogando na fórmula da temperatura:
Já sabemos que será o dobro da pressão do estado inicial, agora precisamos o volume. Usando a relação obtida no passo 1:
Chegamos às coordenadas para o estado final: ().
Se analisarmos a relação entre V e P, , temos uma linearidade. Ou seja, o gás vai de () até () por uma linha reta.
Se jogarmos tudo isso no diagrama:
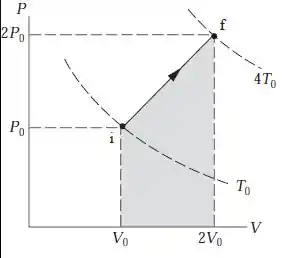
O mais difícil já conseguimos, agora só falta o trabalho.
Passo 3
Segundo a Primeira Lei da Termodinâmica, o trabalho pode ser calculado como a área abaixo do gráfico.
O gráfico é formado uma figura geométrica conhecida, o trapézio. Então o trabalho do gás será:
Vamos definir cada um dos valores:
Jogando no trabalho: