Enunciado
Física - Física para Cientistas e Engenheiros - Mecânica, Oscilações e Ondas, Termodinâmica: Volume 1 - 6ª Edição - Mosca, Tripler- Ed: 6º - Capítulo 18.1 - Ex. 76
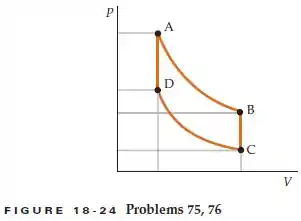
No ponto D da Figura 18-24, a pressão e a temperatura de 2 mol de um gás diatômico ideal são 2 atm e 360 K, respectivamente. O volume do gás no ponto B do diagrama PV é igual a três vezes o volume no ponto D e sua pressão é o dobro da pressão no ponto C. Os caminhos AB e CD representam processos isotérmicos. O gás é conduzido através de um ciclo completo ao longo do caminho DABCD. Determine o trabalho realizado pelo gás e o calor por ele absorvido, em cada etapa do ciclo.
Passo 1
Bom, o exercício nos pede o trabalho realizado pelo gás e o calor por ele absorvido de cada etapa do ciclo. Vamos ver primeiro como calcular o trabalho. Precisamos achar esses 4 valores:
Vocês podem perceber pelo gráfico que o caminho de e não apresenta variação no volume, porque temos segmentos verticais, que começam e acabam no mesmo valor de .
Se não há variação no volume então não há trabalho. Não se esqueçam!
Sendo assim:
Falta calcular
Vamos calcular cada um separadamente.
Passo 2
Começaremos calculando o trabalho do caminho Sabemos do enunciado que esse processo é uma expansão isotérmica. Então a temperatura que ele dá no ponto D vai ser igual a temperatura do ponto :
Em expansões isotérmicas, o trabalho pode ser calculado como:
O problema aqui é que não sabemos nenhum dos volumes. Mas lembra que ele disse que o volume do gás no ponto B do diagrama PV é igual a três vezes o volume no ponto D?
Aí lembra também que de para o volume não muda, então
Legal! Temos uma relação entre e , certo? Então bora substituir:
Substituindo os outros dados
Optamos por começar por esse caminho, porque tínhamos mais informações ao seu respeito. Mas bora achar o próximo.
Passo 3
No caminho não temos a temperatura, mas sabemos que este caminho também é isotérmico, ou seja, podemos achá-la usando o ponto A ou B, de acordo com a equação de estado dos gases:
Não temos quase nada, para achar essas pressões e volumes. O que fazer agora?
Vamos trabalhar com o que temos. Se vocês observarem, nós temos tudo o que precisamos para calcular o volume para o ponto D usando a equação de estado dos gases, porque temos
Assim vamos usar para achar o volume de
Vamos isolá-lo:
E agora substituir os valores, lembrando de passar o que está em para :
Temos que
E que:
Passo 4
Legal! Já achamos todos os volumes. Agora vamos conseguir as pressões. Neste caso podemos usar a equação de estado dos gases para o ponto C, porque é o único ponto, além do D, para o qual temos temperatura e volume:
Isolando:
Substituindo, lembrando de passar o volume para
Passando essa resposta para :
Se sabemos do enunciado que
Temos
Passo 5
Ufa! Fizemos muita coisa, mas agora conseguimos a temperatura do caminho usando os dados para o ponto B:
Substituindo, lembrando de passar volume para e pressão para
Agora sim, temos tudo o que precisamos para calcular o trabalho. Lembrando que para o processo isotérmico, temos:
Substituindo:
Passo 6
Não acabou ainda! Precisamos do calor de cada etapa do ciclo. Vamos por parte. Nos caminhos onde não houve variação de volume, podemos afirmar que não houve trabalho. Aí da primeira lei temos:
Aí a variação da energia pode ser calculada como:
Neste caso, g são os graus de liberdade do gás. Para um gás diatômico, :
Para o caminho
Para o caminho
Passo 7
Nos demais caminhos sua temperatura não se altera. Quando não há variação de temperatura, podemos dizer que , assim a primeira lei fica
Mas lembra que o trabalho realizado sobreo gás é igual ao trabalho realizado pelo gás, mas com sinal inverso, então podemos substituir
Mas por que fazer aparecer ali? Cara, porque a gente já tem esses valores! Lembra que a gente achou o trabalho realizado pelo gás em cada processo. Então ficamos assim
Para
Para