Enunciado
Física - Halliday - Vol 4- Ed: 10º - Capítulo 34.4 - Ex. 46
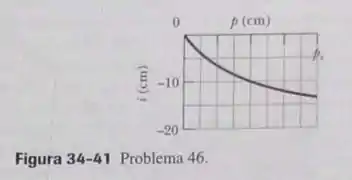
Um objeto é colocado no centro de uma lente delgada e deslocado ao longo do eixo central até uma distância de da lente. Durante o movimento a distância entre a lente e a imagem do objeto é medida. A Fig. 34-41 mostra o resultado em função da distância do objeto até . Determine a distância da imagem para .
Passo 1
Bom, como tem 8 quadrados no gráfico e a distância do zero até é de, cada quadrado vale . Para resolvermos esse problema, vamos precisar da equação de lentes delgadas:
Mas como não temos , a gente tem que usar valores que do gráfico para encontrar o valor dele, que é constante para qualquer parte do gráfico e depois encontrar para
Passo 2
Como dá para ver, quando , é exatamente , então:
Passo 3
E então substituindo o na equação junto com depois de isolar :