Exercícios de Reflexão Total da Luz - Lista de Exercícios Resolvida
Questão 1
Um peixe-gato está abaixo da superfície de um lago.
- Qual é o diâmetro da circunferência na superfície que delimita a região na qual o peixe pode ver o que existe do lado de fora do lago?
- Se o peixe desce para uma profundidade maior, o diâmetro da circunferência aumenta, diminui ou continua o mesmo?
Considere o índice de refração da água .
Ver solução completaQuestão 2
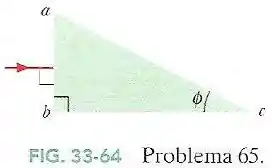
Na Fig.33-64 um raio luminoso incide perpendicularmente à face de um prisma de vidro ().
Determine o maior valor do ângulo para o qual um raio é totalmente refletido na face do prisma se este está imerso:
- No ar
- Na água (cujo índice de refração é )
Questão 3
O índice de refração do benzeno é .
Qual é o ângulo crítico para um raio luminoso que se propaga no benzeno em direção a uma interface plana do benzeno com o ar?
Ver solução completaQuestão 4
Um raio de luz está se propagando em um cubo de vidro que está completamente imerso na água.
Você descobre que, se o raio incide sobre a interface vidro-água em um ângulo maior do que com a normal, nenhuma luz é refratada para dentro da água, cujo índice de refração vale .
Qual é o índice de refração do vidro?
Ver solução completaQuestão 5
A Fig.33-36 mostra quatro placas horizontais , , e feitas de materiais diferentes, com ar acima da primeira placa e abaixo da última. O índice de refração dos materiais é dado.
Raios de luz incidem na extremidade esquerda das quatro placas, da forma indicada na figura.
Em que placa (identifique-a através do índice de refração) existe a possibilidade de que a luz fique confinada de tal forma que, após muitas reflexões, chegue à extremidade direita sem deixar a placa?

Questão 6
A luz entra em um tubo sólido feito de plástico e que possui um índice de refração igual a .
A luz desloca-se paralelamente à parte superior do tubo, conforme a figura abaixo.
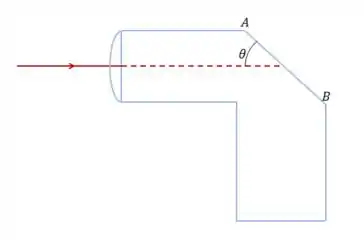
Você deseja cortar a face de modo que toda a luz seja refletida de volta para dentro do tubo depois de atingir essa face.
- Qual é o maior ângulo possível se o tubo está no ar?
- Se o tubo for imerso em água, cujo índice de refração é de , qual é o maior ângulo possível?
Questão 7
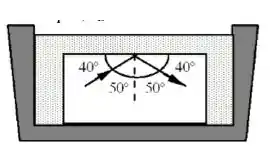
Um bloco de vidro cujo índice de refração vale 1,7 é imerso em um líquido desconhecido. Um raio de luz que se propaga dentro do bloco sobre reflexão interna total como ilustrado na figura. Qual das seguintes relações melhor indica o que se pode concluir a respeito do índice de refração do líquido, ?
Questão 8
Considere uma fibra óptica simples, retilínea, composta por um núcleo cilíndrico de índice de refração , envolvido por uma cascata cilíndrica de índice de refração .
No ponto de entrada da fibra óptica há uma fonte pontual que emite luz em todas as direções, isotropicamente. Sabemos que parte da radiação que entra na fibra é perdida para o exterior.
Suponha que todo raio luminoso que atinge a interface entre os dois meios com ângulo de incidência menor do que o ângulo limite de reflexão total seja totalmente transmitido para o exterior.
Neste caso, se a potência luminosa que entra na fibra é , podemos dizer que a potência perdida pela fibra para o exterior será:
A)
B)
C)
D)
E)
F)
Ver solução completaQuestão 9
Uma fábrica deseja cobrir a superfície plana de um bloco de material translúcido de índice de refração com uma película de material também translúcido de índice de refração .
Contudo, é de fundamental importância verificar como isso afeta o ângulo crítico para a reflexão interna total da luz que, proveniente do interior do bloco, atravessa a película e atinge a interface desta com o ar.
No intervalo de a , para que faixa de ângulos de incidência da luz na interface bloco-película, a luz passa para o ar?
a ;
a ;
a ;
a ;
a ;
a ;
Nenhuma das anteriores;
Ver solução completaQuestão 10
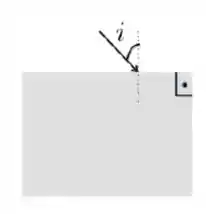
Um feixe de luz propagando-se no ar () incide em uma face horizontal de um paralelepípedo, fazendo um ângulo com a normal, conforme indica a figura abaixo.
Sendo o índice de refração do paralelepípedo , para quais valores de o feixe sofrerá reflexão total na face vertical?
- Nunca haverá reflexão total
Questão 11
O reservatório de metal de lados e representado na figura está totalmente preenchido com um líquido desconhecido. O observador, cujo olho está nivelado com o topo do tanque, pode apenas ver o canto . O índice de refração do presente líquido vale:
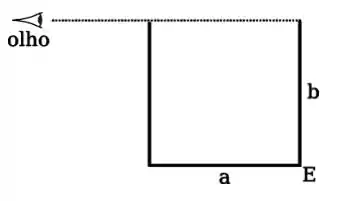
Ver solução completa
Questão 12
Alguns prismas são projetados para que o ângulo de incidência crítico entre o prisma e o ar seja MENOR que . De tal forma ser possível desviar um feixe de sua trajetória original de , sem perda no fluxo de energia cinética incidente. Determine a relação que é sempre válida para o índice de refração desses prismas.
a) .
b) .
c) .
d) .
Ver solução completaQuestão 13
Um feixe de luz parte de um meio material de índice de refração e incide na interface plana entre o material e o ar (), dando origem ao raio refletido apenas. Se o ângulo de incidência é com a normal, a relação válida é.
(a)
(b)
(c)
(d)
(e)
Ver solução completaQuestão 14
Um pequeno corpo luminoso, no fundo de uma piscina de profundidade de água cujo índice de refração é , emite raios para cima em todas as direções.
Uma área circular é formada na superfície da água.
Determinar o raio do círculo de luz.
Questão 15
Uma fonte puntiforme de luz está emitindo luz dentro de um lago transparente e calmo. Sabendo que a fonte está em repouso a uma profundidade e que o índice de refração da água é , podemos afirmar que a luz que pode ser vista na superfície do lago deve:
- Estar esparramado em toda a superfície do lago.
- Estar dentro de um quadrado de lado
- Estar fora de um círculo de raio
- Estar fora de um círculo de raio
- Estar dentro de um círculo de raio
- Nenhuma das respostas acima.