No Problema 6, qual é o módulo da componente (a) horizontal e (b) vertical da força resultante que atua sobre o bloco no ponto ? (c) De que altura o bloco deveria ser liberado, a partir do repouso, para ficar na iminência de perder contato com a superfície no alto do loop? (Iminência de perder o contato significa que a força normal exercida pelo loop sobre o bloco é nula nesse instante.) (d) Plote o módulo da força normal que age sobre o bloco no alto do loop em função da altura inicial , para o intervalo de a .

Com a velocidade em mãos, podemos determinar a força resultante horizontal no ponto aplicando a segunda lei de Newton e lembrando que esta é a resultante centrípeta. Portanto:

Para determinar a força vertical, basta percebermos que nesta direção atua somente a força peso, portanto:

Quando dizemos que o bloco está na iminência de perder o contanto então a normal tende a zero, portanto aplicando a segunda lei de Newton levando em consideração essa suposição no ponto mais alto, encontramos:

Isolando :

Assim, aplicando a conservação da energia mecânica para determinar , temos:

Isolando :

Substituindo o valor de encontrado acima:

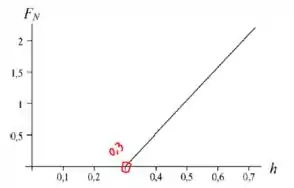
No passo anterior, percebemos que para velocidades menores que a normal é zero, portanto, nossa análise iniciará a partir deste valor. Aplicando a segunda lei de Newton no ponto mais alto para velocidades superiores a descrita acima, temos:

Podemos relacionar a velocidade com a altura usando novamente a conservação da energia mecânica:

Isolando :

Substituindo na expressão da normal:

Portanto, percebemos que a normal varia linearmente e que para valores de a normal é nula: