Suponha que as duas extremidades da barra da Figura 17.23 sejam mantidas à temperatura de e que a distribuição de temperatura inicial ao longo da barra seja dada por , onde é medido a partir da extremidade esquerda da barra. Suponha que a barra seja de cobre, com comprimento , e área da seção reta igual a . a) Mostre a distribuição da temperatura inicial em um diagrama. b) Qual é a distribuição final de temperatura depois de decorrido um intervalo de tempo muito longo? c) Faça um esboço mostrando as curvas que você imagina que possam representar a distribuição de temperatura em tempos intermediários. Qual é o gradiente de temperatura inicial nas extremidades da barra? e) Qual é aa taxa de transferência de calor inicial nas extremidades da barra para os corpos que estão em contato com essas extremidades? f) Qual é a taxa de transferência de calor inicial no centro da barra? Explique. Qual [e a taxa de transferência de calor nesse ponto em qualquer instante posterior? g) Qual é o valor da difusividade térmica para o cobre e quais são as unidades dessa grandeza? (Aqui, é a condutividade térmica, é a densidade e é o calor especifico.) h) Qual é a taxa inicial da variação da temperatura com o tempo no centro da barra? i) Quanto tempo seria necessário para o centro da barra atingir sua temperatura final caso a temperatura continue com essa taxa? (Esse tempo é chamado de tempo de relaxação da barra.) j) Usando os gráficos da parte (c), você esperaria que o modulo da taxa de variação da temperatura no ponto médio permanecesse constante, aumentasse ou diminuísse em função do tempo? k) Qual é a taxa inicial da variação da temperatura em um ponto da barra situado a da sua extremidade esquerda?
Passo 1
a) O gráfico seria a função seno com no intervalo . Se dividirmos a escala de em , para facilitar o desenho do gráfico, o esboço fica:
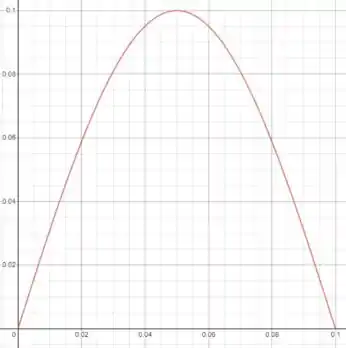
Passo 2
b) Se as extremidades se mantêm a zero graus até o final do período, então a temperatura da barra irá diminuir até que toda a barra esteja a zero graus.
Passo 3
c) Em tempos intermediários, a barra continua com as extremidades a zero graus, e a temperatura do meio da barra, que antes era mais alto, foi transferida para as vizinhanças, então a gente pode dizer que a curva do gráfico vai se tornando cada vez mais suave:
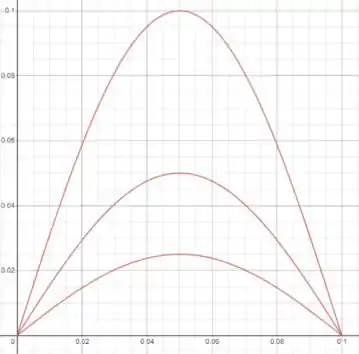
Passo 4
d) O gradiente de temperatura para qualquer ponto, é a derivada da função em relação a :
E como a questão pede nas extremidades, e , em um caso o cosseno será 1 e outro -1, então:
Passo 5
e) A taxa de transferência é dada por:
Usando a condutividade do cobre, a área dada pelo enunciado e o valor da taxa de transferência para as extremidades:
Passo 6
f) O valor da taxa no centro é:
Com , o que resulta zero na função cosseno e na taxa de transferência inteira:
O que faz sentido, já que não há calor passando por aquele ponto quando a barra perde calor para as extremidades, parte flui para a esquerda e, parte para a direita. Isso significa que em momento algum, esse ponto terá corrente de calor.
Passo 7
g) Para esse caso, basta substituirmos os valores dados para o cobre:
Passo 8
h) A taxa da variação de temperatura no centro é dada pela equação de calor:
A segunda derivada da função temperatura é:
No centro , então:
Ficamos com:
Substituindo os valores na equação de calor:
A taxa será:
Passo 9
i) Fazemos a razão entre a temperatura inicial do centro da barra e a taxa de variação:
Usamos o valor positivo da taxa porque o tempo não pode ser negativo.
Passo 10
j) O módulo da variação vai diminuir, podemos ver isso no gráfico da letra (c), à medida que o tempo passa, a curva fica mais suave, e a segunda derivada também vai ficar.
Passo 11
k) Usamos mais uma vez a equação de calor, mas agora usando :
E a taxa nesse ponto vai ser:
Resposta
Ei, a resposta está no passo a passo :)