Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Física - Fundamentos de Física - Mecânica Volume 1 - 10ª Edição - David Halliday, Jearl Walker e Robert Resnick- Ed: 10º - Capítulo 6.1 - Ex. 23

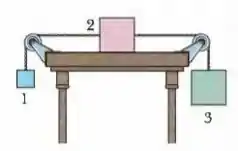
Quando os três blocos da Fig. 6-29 são liberados a partir do repouso, aceleram com um módulo de 0,500   m / s 2 . O bloco 1 tem massa M , o bloco 2 tem massa 2 M e o bloco 3 tem massa 2 M . Qual é o coeficiente de atrito cinético entre o bloco 2 e a mesa?

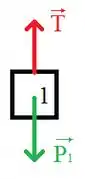
Passo 1

Vamos iniciar essa questão fazendo o DCL de cada bloco:

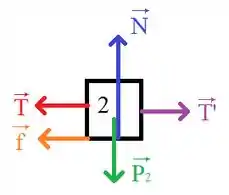
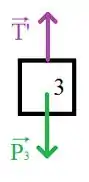
A partir da ilustração podemos aplicar a segunda lei de Newton para cada lego na direção do movimento:

b l o c o   1 :         T - P 1 = m 1 a       e q . 1

b l o c o   2 :         T ' - T - f c = m 2 a       e q . 2

b l o c o   3 :         P 2 - T ' = m 3 a       e q . 3

Passo 2

Vamos isolar o T na e q . 1 :

T = M a + g       e q . 4

De maneira análoga, vamos isolar o T ' na e q . 3 :

T ' = 2 M g - a       e q . 5

Vamos substituir na e q . 2 a e q . 4 e 5 :

2 M g - a - M a + g - f c = 2 M a

Dividindo os dois lados da equação por M :

2 g - 2 a - a - g - f c M = 2 a

g - 3 a - f c M = 2 a

Isolando f c :

f c = M ( g - 5 a )       e q . 7

Passo 3

Vamos lembrar que a força de atrito cinético pode ser calculado por:

f c = μ c N       e q . 8

Para tanto, vamos determinar a normal aplicando a segunda lei de Newton para o eixo perpendicular ao movimento:

N - P 2 = m 2 a y

Como o movimento ocorre exclusivamente no eixo x , então a y = 0 . Assim, isolando N :

N = 2 M g

Assim, reescrevendo a e q . 8 :

f c = μ c   2 M g       e q . 9

Passo 4

Igualando a e q . 7 e a e q . 9 :

M g - 5 a = μ c   2 M g

Dividindo os dois lados por M e isolando μ c :

μ c = g - 5 a 2 g

Substituindo os valores conhecidos:

μ c = 9,8 - 5 × 0,5 2 × 9,8 = 0,37

Resposta

μ c = 0,37

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um barco de 1000k g está navegando a 90k m / h quando o motor é desligado. O módulo da força de atrito f → k entre o barco e a água é proporcional à velocidade v do barco: f k = 70 v , onde v está em
Dois blocos, com 3,6N e 7,2N de peso, estão ligados por uma corda sem massa e deslizam para baixo em um plano inclinado de 30 ° . O coeficiente de atrito cinético entre o bloco mais leve e o plano é 0
Um bloco escorrega para baixo com velocidade constante em um plano inclinado de ângulo θ . Em seguida, o bloco é lançado para cima no mesmo plano com velocidade inicial v 0 . (a) Que distância o bloco
Na Fig. 6-62, um bloco de 5,0k g se move para cima ao longo de um plano inclinado de ângulo θ = 37 ° ao mesmo tempo em que sofre a ação de uma força horizontal F → de módulo 50N . O coeficiente de atr
Um operário aplica uma força constante de módulo 85N a uma caixa de 40k g que está inicialmente em repouso no piso horizontal de um armazém. Após a caixa ter percorrido uma distância de 1,4m , sua vel